卷积（Convolution）是一种数学运算，常用于信号处理和图像处理领域，也在深度学习中的卷积神经网络（CNN）中发挥着关键作用。简单来说，卷积是通过在两个函数之间滑动并在每个位置上计算它们的积分来生成一个新的函数。
在图像处理中，卷积通常用于图像的特征提取。
深度可分离卷积
在《Python深度学习》（Keras之父执笔）这本书里看到：注意，大部分（或全部）普通卷积很可能不久后会被深度可分离卷积(depthwise separable convolution)所替代, 后者与前者等效，但速度更快，表示效率更高。
1. 简介
在可分离卷积中，它将对区域和通道的计算分离开，而普通卷积是同时考虑区域和通道的。
2. 通过例子对比可分离卷积和普通卷积的区别
假设一个3×3大小的filter，其输入通道为16，输出通道为32
普通卷积的参数： （3×3×16）×32=4068
可分离卷积：
先考虑区域，即每个通道对应一个3×3×1大小的filter, 然后考虑通道对应32个1×1×16大小的filter
参数计算： （3×3×1）×16 + （1×1×16）×32=656
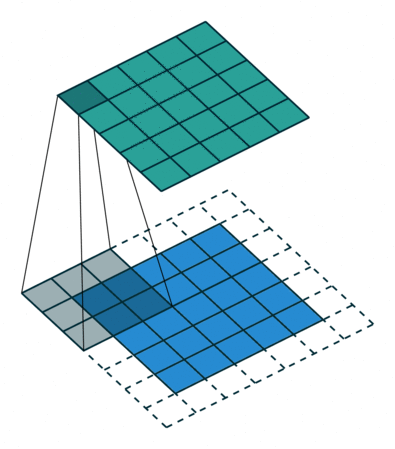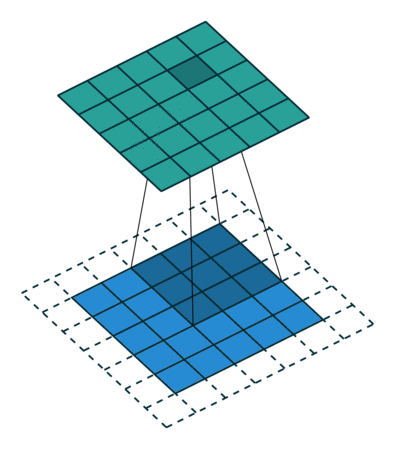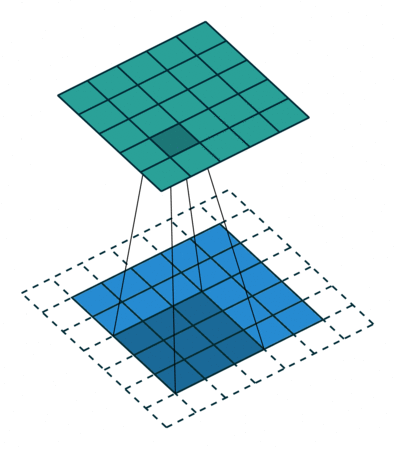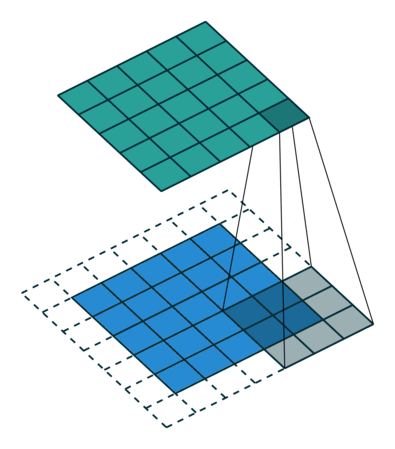
下面这张图来自参考链接1
深度学习中的卷积
当提到神经网络中的卷积时，我们通常是指由多个并行卷积组成的运算。（因为单个核只能特区一种类型的特征，我们usually希望可以在多个位置提取多个特征）
输入也不仅仅是实值的网格，而是由一系列观测数据的向量构成的网格。
我们有的时候会希望跳出核中的一些位置来降低计算的开销（相应的代价是提取特征没有先前那么好了）我们就把这个过程看作对全卷积函数输出的下采样(downsampling).如果只是在输出的每个方向上每间隔s个像素进行采样，那么可重新定义一个 下采样卷积函数。我们把s称为下采样卷积的步幅（stride）。
在任何卷积网络的实现中都有一个重要性质：能够隐含地对输入V用零进行填充（pad）使得它加宽。
普遍意义的卷积
从数学上讲，卷积只不过是一种运算，对于很多没有学过信号处理，自动控制的同学来说各种专业的名词可以不做了解。我们接着继续：
在传统的神经网络中，比如多层感知机（MLP），其输入通常是一个特征向量。需要人工设计特征，然后将用这些特征计算的值组成特征向量。在过去几十年的经验来看，人工找的特征并不总是好用。有时多了，有时少了，有时选的特征根本就不起作用（真正起作用的特征在浩瀚的未知里）。这就是为啥过去几十年神经网络一直被SVM等完虐的原因。
卷积神经网络作为深度学习的典型网络，在图像处理和计算机视觉等多个领域都取得了很好的效果。
Paul-Louis Pröve在Medium上通过这篇文章快速地介绍了不同类型的卷积结构（Convolution）及优势。为了简单起见，本文仅探讨二维卷积结构。
卷积
首先，定义下卷积层的结构参数。
卷积核大小（Kernel Size）：定义了卷积操作的感受野。在二维卷积中，通常设置为3，即卷积核大小为3×3。
步幅（Stride）：定义了卷积核遍历图像时的步幅大小。其默认值通常设置为1，也可将步幅设置为2后对图像进行下采样，这种方式与最大池化类似。