在本篇我们会讨论HMM模型最后一个问题的求解，即即给定模型和观测序列，求给定观测序列条件下，最可能出现的对应的隐藏状态序列。在阅读本篇前，建议先阅读这个系列的第一篇以熟悉HMM模型。
HMM模型的解码问题最常用的算法是维特比算法，当然也有其他的算法可以求解这个问题。同时维特比算法是一个通用的求序列最短路径的动态规划算法，也可以用于很多其他问题。
本文关注于用维特比算法来解码HMM的的最可能隐藏状态序列。
1. HMM最可能隐藏状态序列求解概述
在HMM模型的解码问题中，给定模型 λ = ( A , B , Π ) 和观测序列 O = { o1 , o2 , ... oT } ，求给定观测序列 O 条件下，最可能出现的对应的状态序列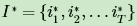
, 即 P ( I ∗ | O ) 要最大化。
一个可能的近似解法是求出观测序列O在每个时刻t最可能的隐藏状态
然后得到一个近似的隐藏状态序列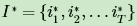。要这样近似求解不难，利用隐马尔科夫模型HMM（二）前向后向算法评估观察序列概率中第五节的定义：在给定模型 λ 和观测序列 O 时，在时刻 t 处于状态 qi 的概率是 γt( i ) ，这个概率可以通过HMM的前向算法与后向算法计算。这样我们有：
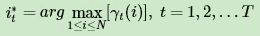
近似算法很简单，但是却不能保证预测的状态序列是整体是最可能的状态序列，因为预测的状态序列中某些相邻的隐藏状态可能存在转移概率为0的情况。
而维特比算法可以将HMM的状态序列作为一个整体来考虑，避免近似算法的问题，下面我们来看看维特比算法进行HMM解码的方法。
2. 维特比算法概述
维特比算法是一个通用的解码算法，是基于动态规划的求序列最短路径的方法。
既然是动态规划算法，那么就需要找到合适的局部状态，以及局部状态的递推公式。在HMM中，维特比算法定义了两个局部状态用于递推。
第一个局部状态是在时刻 t 隐藏状态为 i 所有可能的状态转移路径 i1 , i2 , ...it 中的概率最大值。记为 δt( i ) :
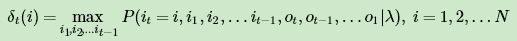
由 δt( i ) 的定义可以得到 δ 的递推表达式：
第二个局部状态由第一个局部状态递推得到。我们定义在时刻t隐藏状态为i的所有单个状态转移路径 ( i1 , i2 , ... , it−1 , i ) 中概率最大的转移路径中第t−1个节点的隐藏状态为 Ψt( i ) , 其递推表达式可以表示为：
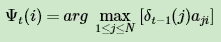
有了这两个局部状态，我们就可以从时刻0一直递推到时刻T，然后利用Ψt(i)记录的前一个最可能的状态节点回溯，直到找到最优的隐藏状态序列。
3. 维特比算法流程总结
现在我们来总结下维特比算法的流程：
输入：HMM模型 λ = ( A , B , Π ) ，观测序列 O = ( o1 , o2 , ... oT )
输出：最有可能的隐藏状态序列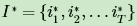
1）初始化局部状态：
2) 进行动态规划递推时刻t=2,3,...T时刻的局部状态：
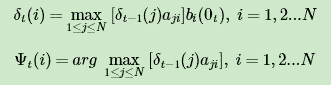
3) 计算时刻T最大的 δT( i ) ,即为最可能隐藏状态序列出现的概率。计算时刻T最大的 Ψt( i ) , 即为时刻T最可能的隐藏状态。
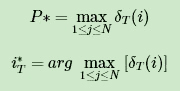
4) 利用局部状态 Ψ ( i ) 开始回溯。对于 t = T−1 , T−2 , ... , 1 ：
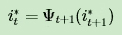
最终得到最有可能的隐藏状态序列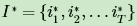
4. HMM维特比算法求解实例
下面我们仍然用隐马尔科夫模型HMM（一）HMM模型中盒子与球的例子来看看HMM维特比算法求解。
我们的观察集合是:
我们的状态集合是：
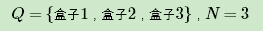
而观察序列和状态序列的长度为3.
初始状态分布为：
状态转移概率分布矩阵为：
观测状态概率矩阵为：
球的颜色的观测序列：
按照我们上一节的维特比算法，首先需要得到三个隐藏状态在时刻1时对应的各自两个局部状态，此时观测状态为1：
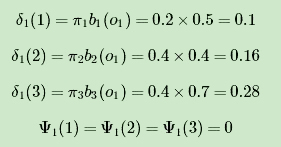
现在开始递推三个隐藏状态在时刻2时对应的各自两个局部状态，此时观测状态为2：
继续递推三个隐藏状态在时刻3时对应的各自两个局部状态，此时观测状态为1：
5. HMM模型维特比算法总结
如果大家看过之前写的文本挖掘的分词原理中的维特比算法，就会发现这两篇之中的维特比算法稍有不同。主要原因是在中文分词时，我们没有观察状态和隐藏状态的区别，只有一种状态。但是维特比算法的核心是定义动态规划的局部状态与局部递推公式，这一点在中文分词维特比算法和HMM的维特比算法是相同的，也是维特比算法的精华所在。
维特比算法也是寻找序列最短路径的一个通用方法，和dijkstra算法有些类似，但是dijkstra算法并没有使用动态规划，而是贪心算法。同时维特比算法仅仅局限于求序列最短路径，而dijkstra算法是通用的求最短路径的方法。
（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）
本文转自：博客园 - 刘建平Pinard，转载此文目的在于传递更多信息，版权归原作者所有。
