简单理解LSTM神经网络

递归神经网络

在传统神经网络中，模型不会关注上一时刻的处理会有什么信息可以用于下一时刻，每一次都只会关注当前时刻的处理。举个例子来说，我们想对一部影片中每一刻出现的事件进行分类，如果我们知道电影前面的事件信息，那么对当前时刻事件的分类就会非常容易。实际上，传统神经网络没有记忆功能，所以它对每一刻出现的事件进行分类时不会用到影片已经出现的信息，那么有什么方法可以让神经网络能够记住这些信息呢？答案就是Recurrent Neural Networks（RNNs）递归神经网络。

递归神经网络的结果与传统神经网络有一些不同，它带有一个指向自身的环，用来表示它可以传递当前时刻处理的信息给下一时刻使用，结构如下：

其中， X_t 为输入，A 为模型处理部分， h_t 为输出。

为了更容易地说明递归神经网络，我们把上图展开，得到：

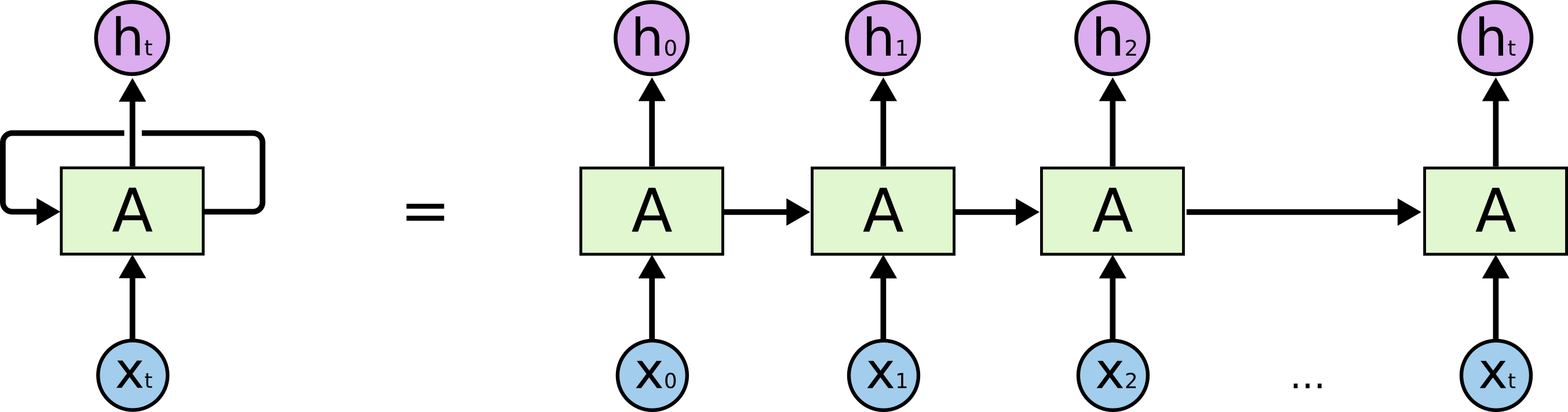
这样的一条链状神经网络代表了一个递归神经网络，可以认为它是对相同神经网络的多重复制，每一时刻的神经网络会传递信息给下一时刻。如何理解它呢？假设有这样一个语言模型，我们要根据句子中已出现的词预测当前词是什么，递归神经网络的工作原理如下：

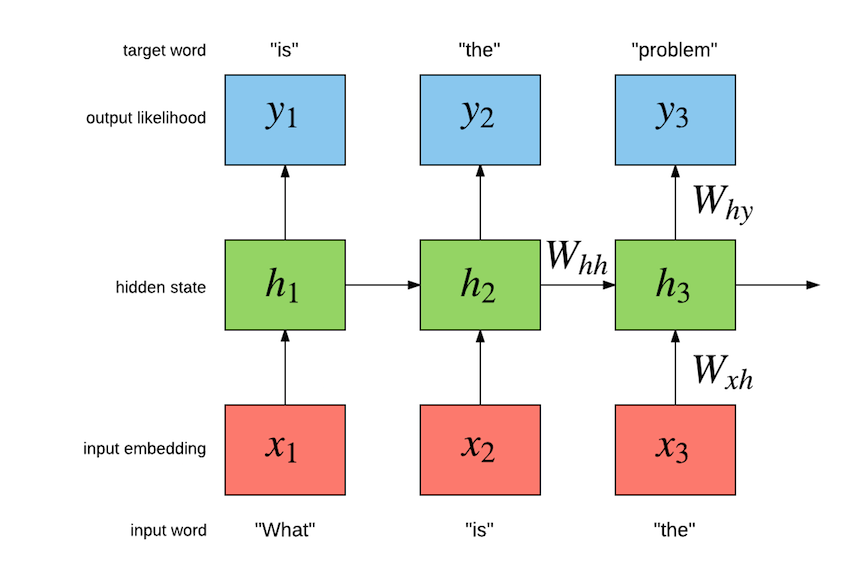
其中，W 为各类权重，x 表示输入，y 表示输出，h 表示隐层处理状态。

递归神经网络因为具有一定的记忆功能，可以被用来解决很多问题，例如：语音识别、语言模型、机器翻译等。但是它并不能很好地处理长时依赖问题。

长时依赖问题

长时依赖是这样的一个问题，当预测点与依赖的相关信息距离比较远的时候，就难以学到该相关信息。例如在句子”我出生在法国，……，我会说法语“中，若要预测末尾”法语“，我们需要用到上下文”法国“。理论上，递归神经网络是可以处理这样的问题的，但是实际上，常规的递归神经网络并不能很好地解决长时依赖，好的是LSTMs可以很好地解决这个问题。

LSTM 神经网络

Long Short Term Mermory network（LSTM）是一种特殊的RNNs，可以很好地解决长时依赖问题。那么它与常规神经网络有什么不同？
首先我们来看RNNs具体一点的结构：

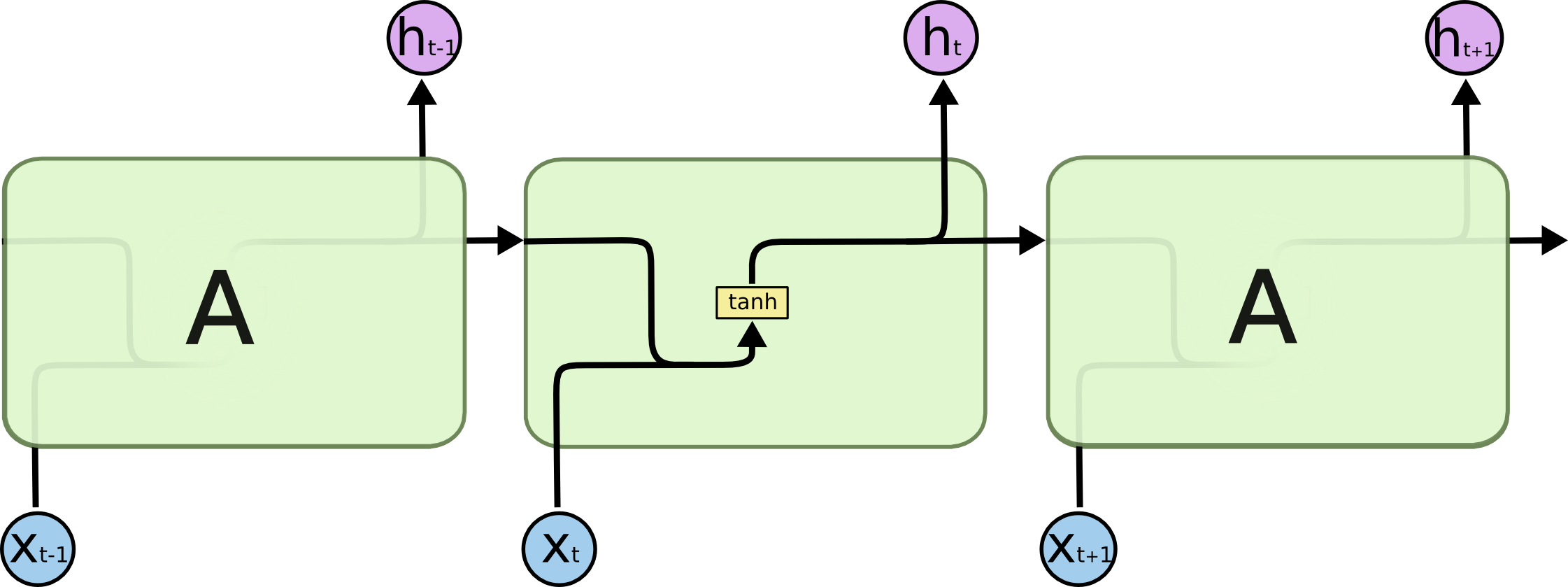
所有的递归神经网络都是由重复神经网络模块构成的一条链，可以看到它的处理层非常简单，通常是一个单tanh层，通过当前输入及上一时刻的输出来得到当前输出。与神经网络相比，经过简单地改造，它已经可以利用上一时刻学习到的信息进行当前时刻的学习了。

LSTM的结构与上面相似，不同的是它的重复模块会比较复杂一点，它有四层结构：

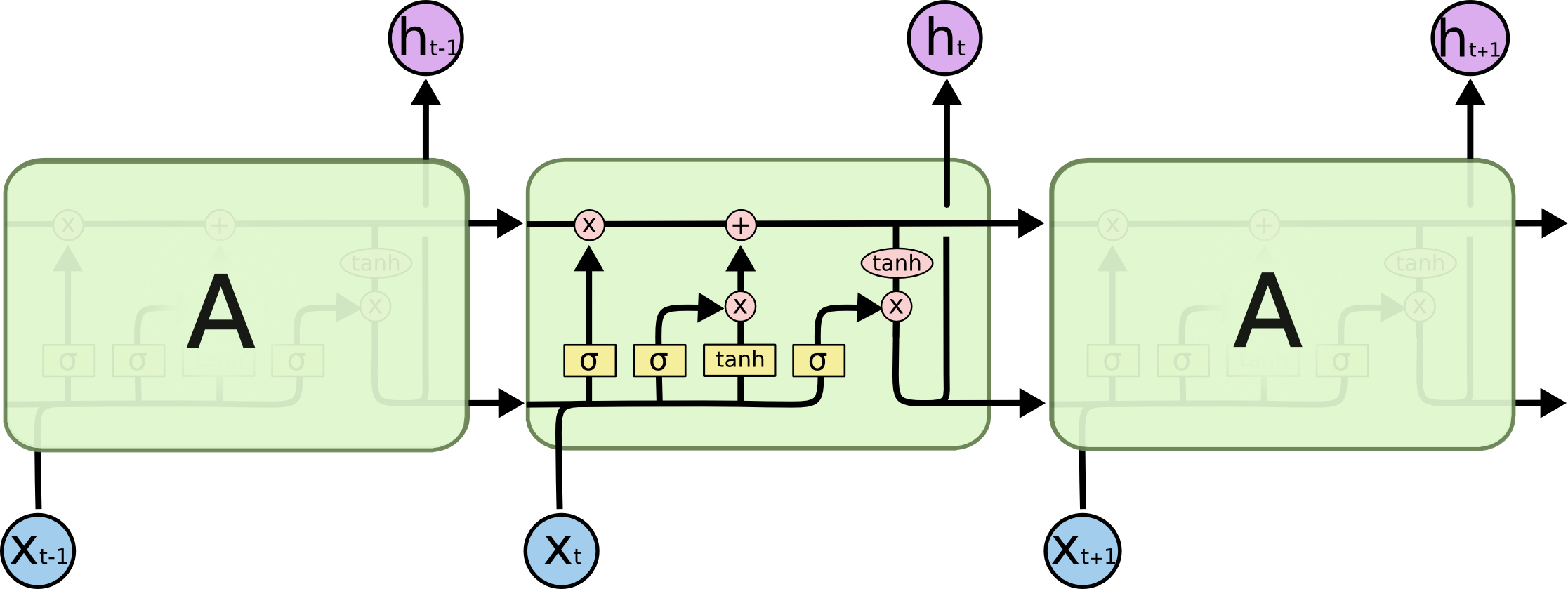
其中，处理层出现的符号及表示意思如下：

LSTMs的核心思想

理解LSTMs的关键就是下面的矩形方框，被称为memory block（记忆块），主要包含了三个门（forget gate、input gate、output gate）与一个记忆单元（cell）。方框内上方的那条水平线，被称为cell state（单元状态），它就像一个传送带，可以控制信息传递给下一时刻。

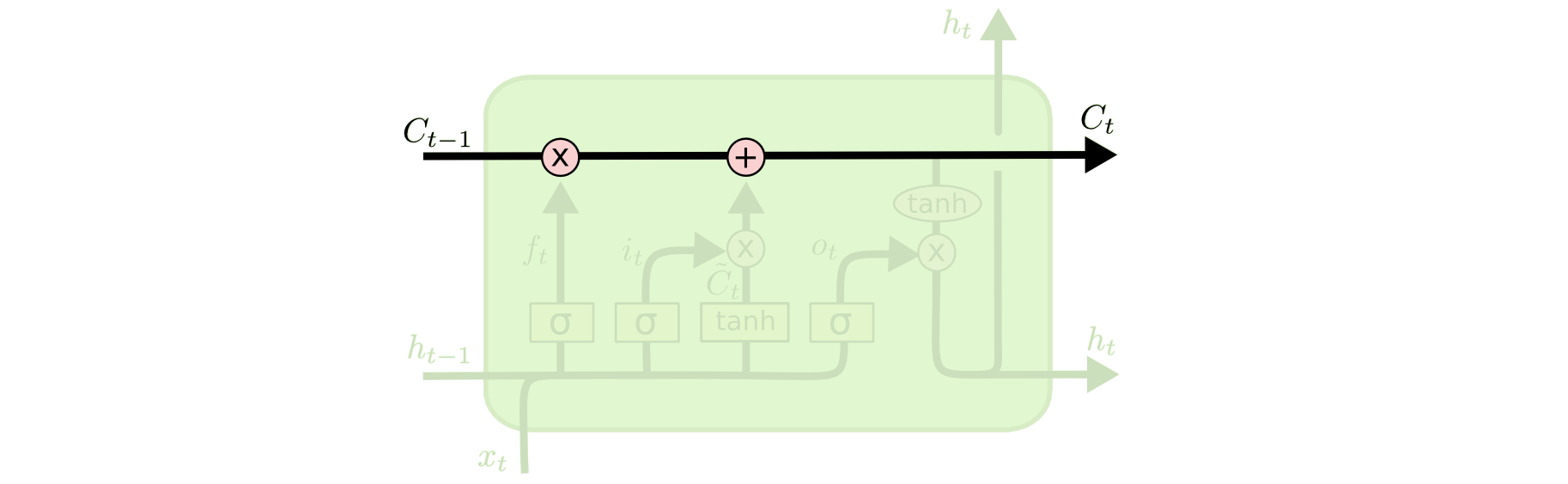
这个矩形方框还可以表示为：

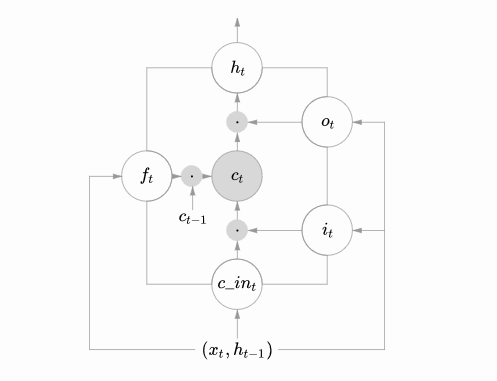
这两个图可以对应起来看，下图中心的 c_t 即cell，从下方输入（ h_{t−1 , xt ）到输出 ht的一条线即为cell state， ft，it，ot 分别为遗忘门、输入门、输出门，用sigmoid层表示。上图中的两个tanh层则分别对应cell的输入与输出。}

LSTM可以通过门控单元可以对cell添加和删除信息。通过门可以有选择地决定信息是否通过，它有一个sigmoid神经网络层和一个成对乘法操作组成，如下：

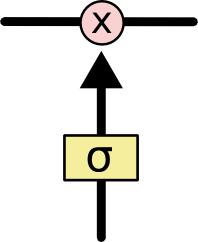
该层的输出是一个介于0到1的数，表示允许信息通过的多少，0 表示完全不允许通过，1表示允许完全通过。

逐步解析LSTM

LSTM第一步是用来决定什么信息可以通过cell state。这个决定由“forget gate”层通过 sigmoid 来控制，它会根据上一时刻的输出 h_t−1 和当前输入 x_t 来产生一个0到1 的 f_t 值，来决定是否让上一时刻学到的信息 C_t−1 通过或部分通过。如下：

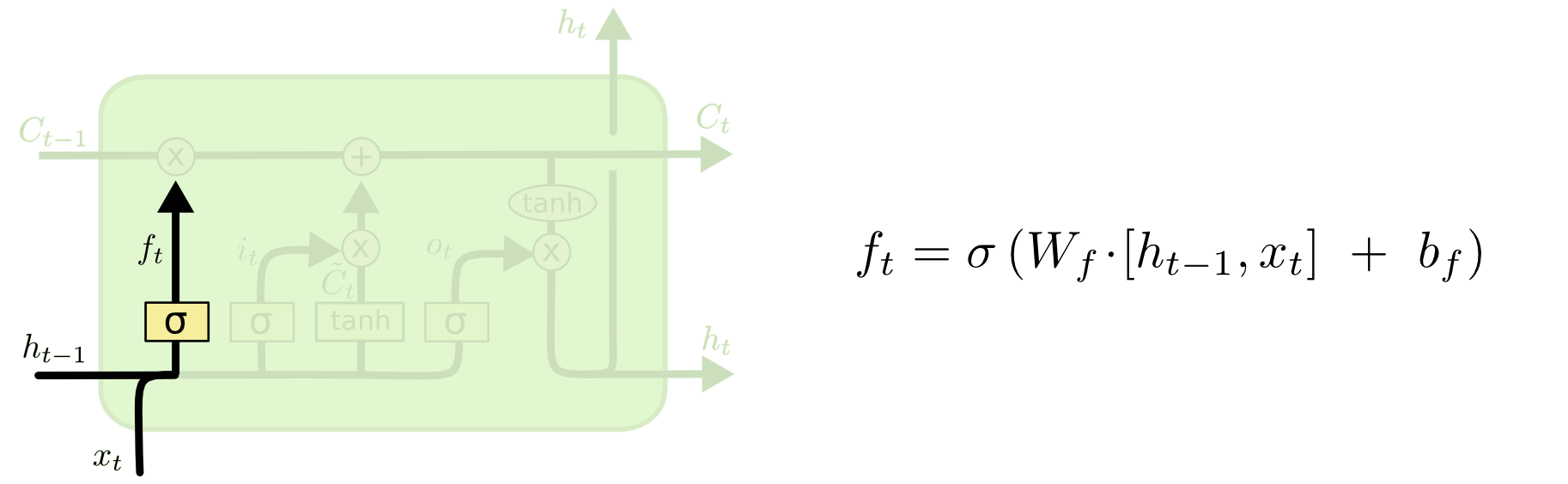
举个例子来说就是，我们在之前的句子中学到了很多东西，一些东西对当前来讲是没用的，可以对它进行选择性地过滤。

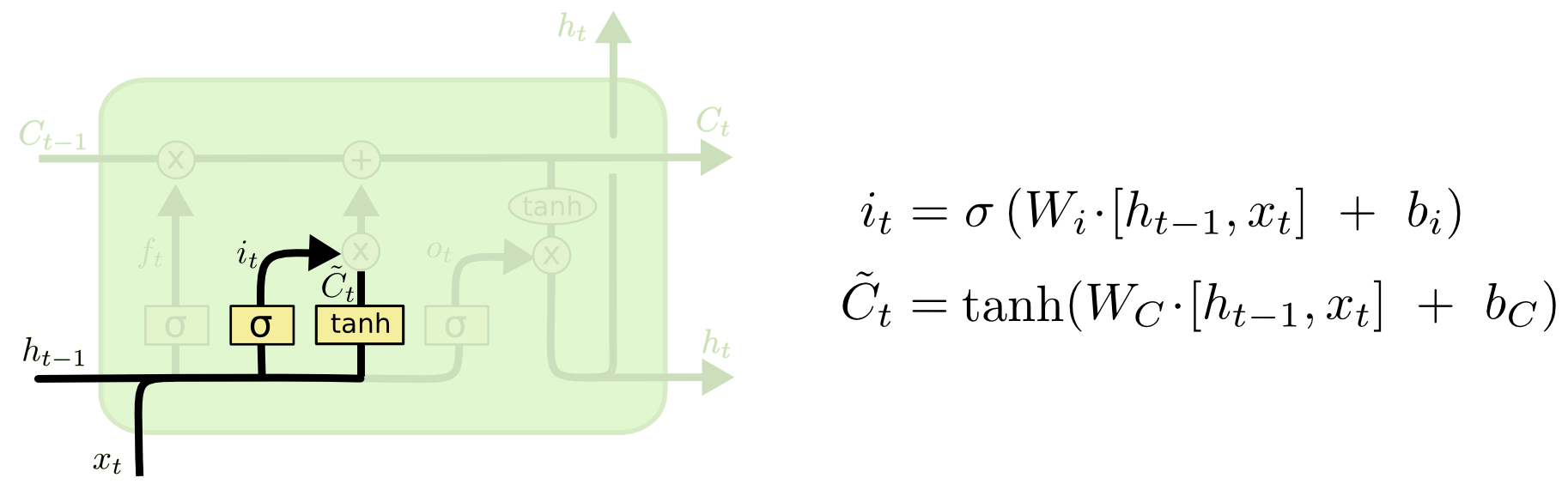
第二步是产生我们需要更新的新信息。这一步包含两部分，第一个是一个“input gate”层通过sigmoid来决定哪些值用来更新，第二个是一个tanh层用来生成新的候选值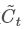，它作为当前层产生的候选值可能会添加到cell state中。我们会把这两部分产生的值结合来进行更新。

现在我们对老的cell state进行更新，首先，我们将老的cell state乘以 f_t 来忘掉我们不需要的信息，然后再与 i_t ∗ 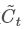相加，得到了候选值。
一二步结合起来就是丢掉不需要的信息，添加新信息的过程：

举个例子就是，在前面的句子中我们保存的是张三的信息，现在有了新的李四信息，我们需要把张三的信息丢弃掉，然后把李四的信息保存下来。

最后一步是决定模型的输出，首先是通过sigmoid层来得到一个初始输出，然后使用tanh将 C_t 值缩放到-1到1间，再与sigmoid得到的输出逐对相乘，从而得到模型的输出。

这显然可以理解，首先sigmoid函数的输出是不考虑先前时刻学到的信息的输出，tanh函数是对先前学到信息的压缩处理，起到稳定数值的作用，两者的结合学习就是递归神经网络的学习思想。至于模型是如何学习的，那就是后向传播误差学习权重的一个过程了。

上面是对LSTM一个典型结构的理解，当然，它也会有一些结构上的变形，但思想基本不变，这里也就不多讲了。

参考：http://colah.github.io/posts/2015-08-Understanding-LSTMs/
版权声明：本文为CSDN博主（火贪三刀）原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
原文链接：https://blog.csdn.net/shijing_0214/article/details/52081301