作者: 左右Shawn
来源:智能算法
卷积现在可能是深度学习中最重要的概念。正是靠着卷积和卷积神经网络,深度学习才超越了几乎其他所有的机器学习手段。这期我们一起学习下深度学习中常见的卷积有哪些?
1. 一般卷积
卷积在数学上用通俗的话来说就是输入矩阵与卷积核(卷积核也是矩阵)进行对应元素相乘并求和,所以一次卷积的结果的输出是一个数,最后对整个输入输入矩阵进行遍历,最终得到一个结果矩阵,说白了就是一个卷积核在图像上滑动,并求取对应元素相乘求和的过程,如下图:
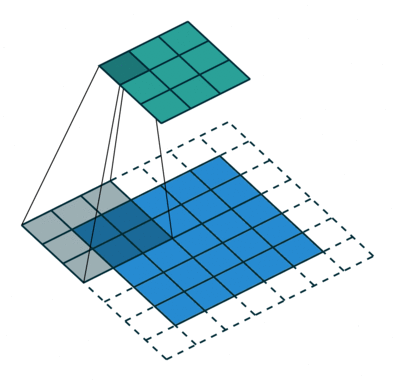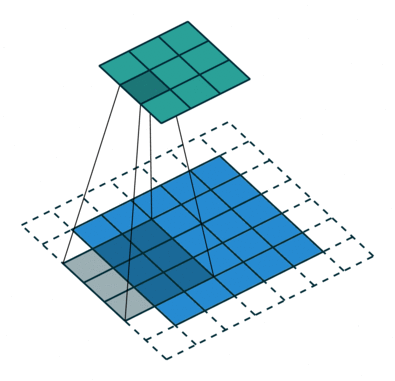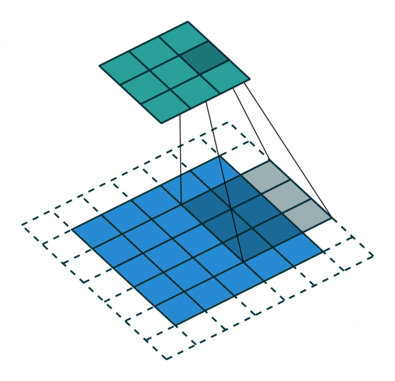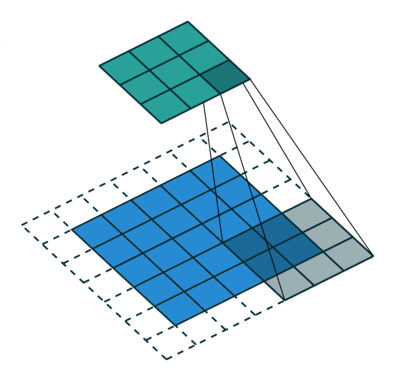
首先,一般情况下卷积层的作用都是用来自动提取图像的一些视觉特征,代替传统的手动方法提取特征不精确,不全面等缺点。常见的一般卷积操作都包括以下四个参数:
卷积核大小(Kernel Size):卷积核定义了卷积的大小范围,在网络中代表感受野的大小,二维卷积核最常见的就是 3*3 的卷积核,也可以根据网络设计5*5或者7*7,甚至1*1等不同size的卷积核,来提取不同尺度的特征。
在卷积神经网络中,一般情况下,卷积核越大,感受野(receptive field)越大,看到的图片信息越多,所获得的全局特征越好。虽说如此,但是大的卷积核会导致计算量的暴增,不利于模型深度的增加,计算性能也会降低。如上图中卷积核的size为3*3.
步长(Stride):卷积核的步长度代表提取的精度, 步长定义了当卷积核在图像上面进行卷积操作的时候,每次卷积跨越的长度。在默认情况下,步长通常为 1,但我们也可以采用步长是 2 的下采样过程,类似于 MaxPooling 操作。
对于size为3的卷积核,如果step为1,那么相邻步感受野之间就会有重复区域;如果step为2,那么相邻感受野不会重复,也不会有覆盖不到的地方;如果step为3,那么相邻步感受野之间会有一道大小为1颗像素的缝隙,从某种程度来说,这样就遗漏了原图的信息。
填充(Padding):卷积核与图像尺寸不匹配,往往填充图像缺失区域,如上图,原始图片尺寸为5*5,卷积核的大小为3*3,如果不进行填充,步长为1的话,当卷积核沿着图片滑动后只能滑动出一个3*3的图片出来,这就造成了卷积后的图片和卷积前的图片尺寸不一致,这显然不是我们想要的结果,所以为了避免这种情况,需要先对原始图片做边界填充处理。
输入和输出通道数(Input & Output Channels):卷积核的输入通道数(in depth)由输入矩阵的通道数所决定;输出矩阵的通道数(out depth)由卷积核的输出通道数所决定。每一层卷积有多少channel数,以及一共有多少层卷积,这些暂时没有理论支撑,一般都是靠感觉去设置几组候选值,然后通过实验挑选出其中的最佳值。这也是现在深度卷积神经网络虽然效果拔群,但是一直为人诟病的原因之一。
2. 扩张卷积

扩张卷积(Dilated Convolution)也被称为空洞卷积或者膨胀卷积,是在标准的卷积核中注入空洞,以此来增加模型的感受野(reception field)。相比原来的正常卷积操作,除了卷积核大小,步长和填充外,扩张卷积多了一个参数:dilation rate,指的是卷积核的点的间隔数量,比如常规的卷积操作dilatation rate为1。扩张的卷积为卷积层引入另一个参数,称为扩张率。这定义了卷积核中值之间的间距。扩张率为2的3x3内核与5x5内核具有相同的视野,而仅使用9个参数。想象一下,获取一个5x5内核并删除每一个第二列和第二行(间隔删除)。
如之前的一篇文章:为什么要用空洞卷积?
如下图,正常卷积核空洞卷积对比:
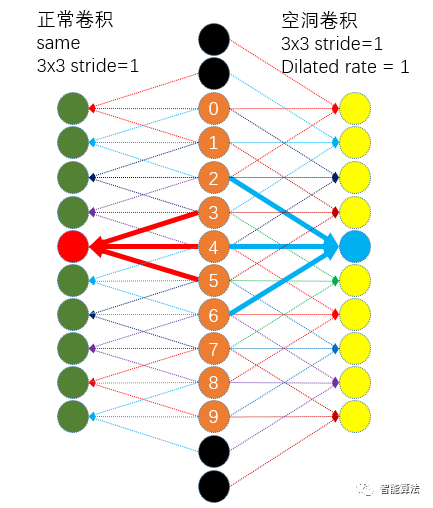
上图左侧为对0-9共10颗像素的正常3x3卷积,padding为same,stride=1的情况下,我们知道其卷积后共得到10个特征,每个特征的感受野均为3x3,如左侧红色的那个特征覆盖3,4,5三颗像素(想象二维情况下应该是3x3)。
上图右侧为对0-9共10颗像素的空洞3x3卷积,这里的3x3是指有效区域,在padding为same,stride=1的情况下,也得到了10个特征,但是每个特征的感受野为5x5,如右侧蓝色的那个特征覆盖2,3,4,5,6五颗像素(想象二维情况下应该是5x5)。
这就在不丢失特征分辨率的情况下扩大了感受野,进而对检测大物体有比较好的效果。所以总的来说,空洞卷积主要作用:不丢失分辨率的情况下扩大感受野;调整扩张率获得多尺度信息。但是对于一些很小的物体,本身就不要那么大的感受野来说,这就不那么友好了。
3. 转置卷积
转置卷积又叫反卷积、逆卷积。不过转置卷积是目前最为正规和主流的名称,因为这个名称更加贴切的描述了卷积的计算过程,而其他的名字容易造成误导。在主流的深度学习框架中,如TensorFlow,Pytorch,Keras中的函数名都是conv_transpose。所以学习转置卷积之前,我们一定要弄清楚标准名称,遇到他人说反卷积、逆卷积也要帮其纠正,让不正确的命名尽早的淹没在历史的长河中。
有大佬一句话总结:转置卷积相对于卷积在神经网络结构的正向和反向传播中做相反的运算。其实还是不是很理解。我们先从转置卷积的用途来理解下,转置卷积通常用于几个方面:
① CNN可视化,通过反卷积将卷积得到的feature map还原到像素空间,来观察feature map对哪些pattern相应最大,即可视化哪些特征是卷积操作提取出来的;
② FCN全卷积网络中,由于要对图像进行像素级的分割,需要将图像尺寸还原到原来的大小,类似upsampling的操作,所以需要采用反卷积;
③ GAN对抗式生成网络中,由于需要从输入图像到生成图像,自然需要将提取的特征图还原到和原图同样尺寸的大小,即也需要反卷积操作。
我们先来看看卷积和反卷积的图,简直不要太形象。
如下图正常卷积(convolution):
卷积核为 3x3;no padding , strides=1

转置卷积可以理解为upsample conv.如下图:
卷积核为:3x3; no padding , strides=1
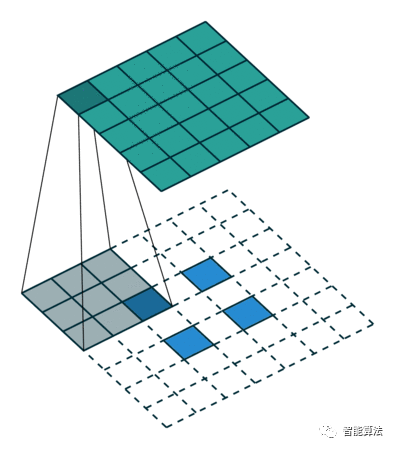
从上面两个图可以看到,转置卷积和卷积有点类似,因为它产生与假设的反卷积层相同的空间分辨率。但是,对值执行的实际数学运算是不同的。转置卷积层执行常规卷积,但恢复其空间变换。 需要注意的是:反卷积只能恢复尺寸,不能恢复数值。
4. 可分离卷积
任何看过MobileNet架构的人都会遇到可分离卷积(separable convolutions)这个概念。但什么是“可分离卷积”,它与标准的卷积又有什么区别?可分离卷积主要有两种类型:空间可分离卷积和深度可分离卷积。
空间可分离卷积
在可分离的卷积中,我们可以将内核操作分成多个步骤。让我们将卷积表示为y = conv(x,k),其中y是输出图像,x是输入图像,k是核。简单。接下来,假设k可以通过以下公式计算:k = k1.dot(k2)。这将使它成为可分离的卷积,因为我们可以通过用k1和k2进行2个1D卷积来得到相同的结果,而不是用k进行2D卷积。

以Sobel内核为例,它通常用于图像处理。你可以通过乘以向量[1,0,-1]和[1,2,1] .T得到相同的内核。在执行相同操作时,这将需要6个而不是9个参数。上面的例子显示了所谓的空间可分卷积。
空间可分卷积的主要问题是并非所有卷积核都可以“分离”成两个较小的卷积核。这在训练期间变得特别麻烦,因为网络可能采用所有可能的卷积核,它最终只能使用可以分成两个较小卷积核的一小部分。
实际上,通过堆叠1xN和Nx1内核层,可以创建与空间可分离卷积非常相似的东西。这最近在一个名为EffNet的架构中使用,显示了有希望的结果。
深度可分离卷积
在神经网络中,我们通常使用称为深度可分离卷积的东西。这将执行空间卷积,同时保持通道分离,然后进行深度卷积。这里,通过一个例子可以最好地理解它(以下参考文献2):
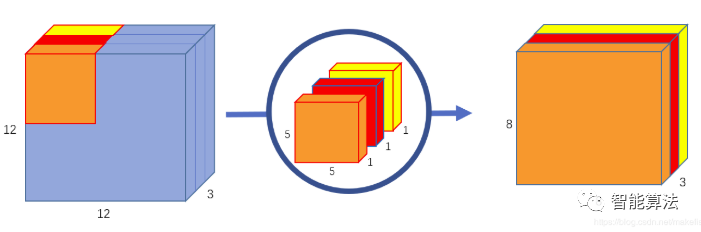
以输入图像为12x12x3的RGB图像为例,正常卷积是卷积核对3个通道同时做卷积。也就是说,3个通道,在一次卷积后,输出一个数。而深度可分离卷积分为两步:
- 第一步用三个卷积对三个通道分别做卷积,这样在一次卷积后,输出3个数。
- 这输出的三个数,再通过一个1x1x3的卷积核(pointwise核),得到一个数。
所以深度可分离卷积其实是通过两次卷积实现的。
第一步,对三个通道分别做卷积,输出三个通道的属性,如下图:
第二步,用卷积核1x1x3对三个通道再次做卷积,这个时候的输出就和正常卷积一样,是8x8x1:

如果要提取更多的属性,则需要设计更多的1x1x3卷积核心就可以(图片引用自原网站。感觉应该将8x8x256那个立方体绘制成256个8x8x1,因为他们不是一体的,代表了256个属性):

可以看到,如果仅仅是提取一个属性,深度可分离卷积的方法,不如正常卷积。随着要提取的属性越来越多,深度可分离卷积就能够节省更多的参数。
文献1:https://zhuanlan.zhihu.com/p/28186857
文献2:https://blog.csdn.net/makefish/article/details/88716534
本文转自: 智能算法 ,作者:左右Shawn
转载此文目的在于传递更多信息,版权归原作者所有。