Gouraud Shading和Phong Shading都是光照反射模型(Reflection Model),用来计算镜面反射方向的光强。
注意,不要望文生义,认为是计算阴影的模型。
相同点:
1. 二者都是明暗处理技术;
2. 都要先应用多边形的法线算出其公共顶点的法线(如下图);
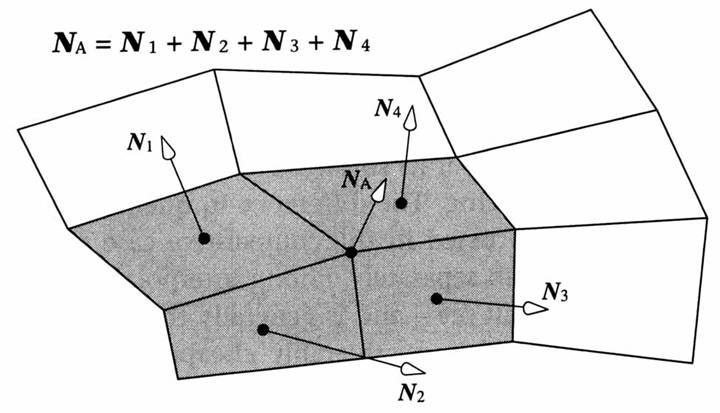
3. 都应用Phong局部反射模型计算多边形顶点处的光强(算式如下图)。
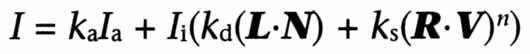
即 反射光 = 环境光 + 漫反射 + 镜面反射
其中环境光是一个常量,就好比将一条直线上移的截距值,基于这个基本光强,再加上漫反射和镜面反射。
漫反射和镜面反射是点光源在该点上的漫反射和镜面反射。
4. 都不考虑物体间的相互作用,即将物体的反射光、折射光(漫反射光实际上是上头提到的环境光,我们将其看成常量处理,比较简单)作为入射光强的一部分来考虑,这样是相对不真实的情况,ray tracing会解决这一问题。
下图为Phong局部反射模型中漫反射和镜面反射的示意图:
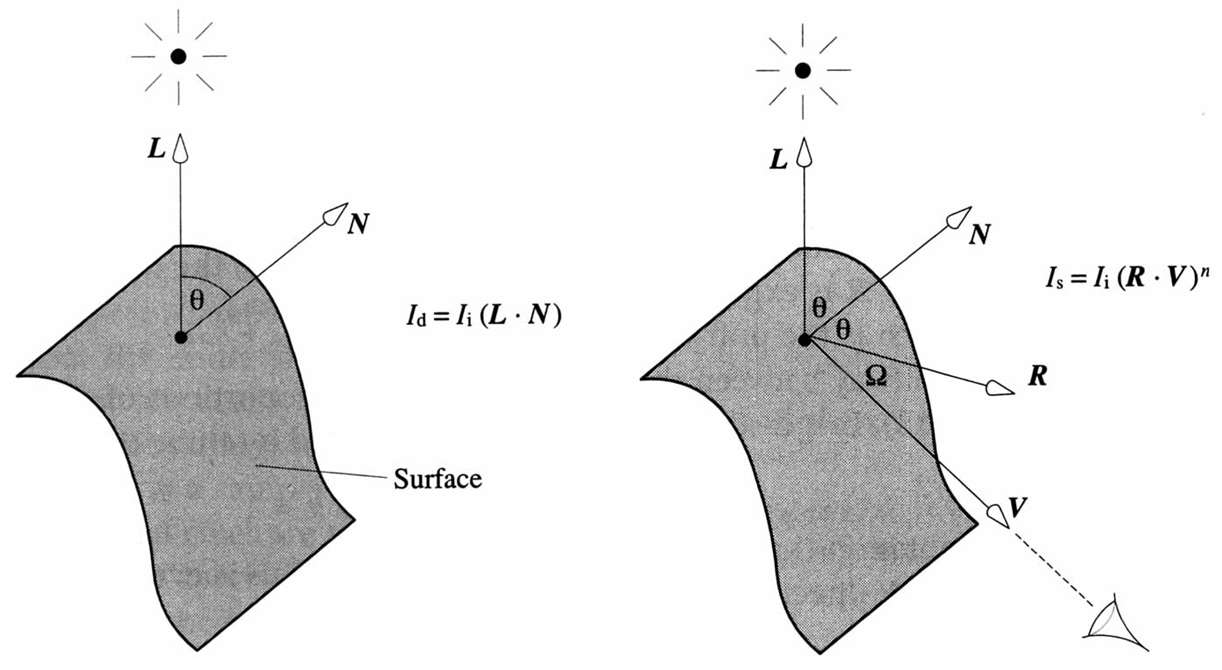
不同点:
Gouraud明暗处理只在多边形顶点处采用Phong局部反射模型计算光强,而在多边形内的其他点采用双向线性插值,这样做的优点是高效,但是无法很好的处理镜面高光问题,依赖于其所在多面形的相对位置;
而Phong明暗处理,通过差值计算每个顶点的法向量(3次差值,在x,y,z三个方向分别进行差值计算),然后计算每个点上的光强值,这样效果好,但计算复杂,需要付出比Gouraud 4-5 倍的时间。
通常,在一个比较复杂的场景中,当物体镜面发射很微弱时,我们对其采用Gouraud明暗处理,而对于一些镜面高光的物体,采用Phong明暗处理,这样既保证质量,又保证速度。
下图为Gouraud (a)和Phong (b)模型的示意图:
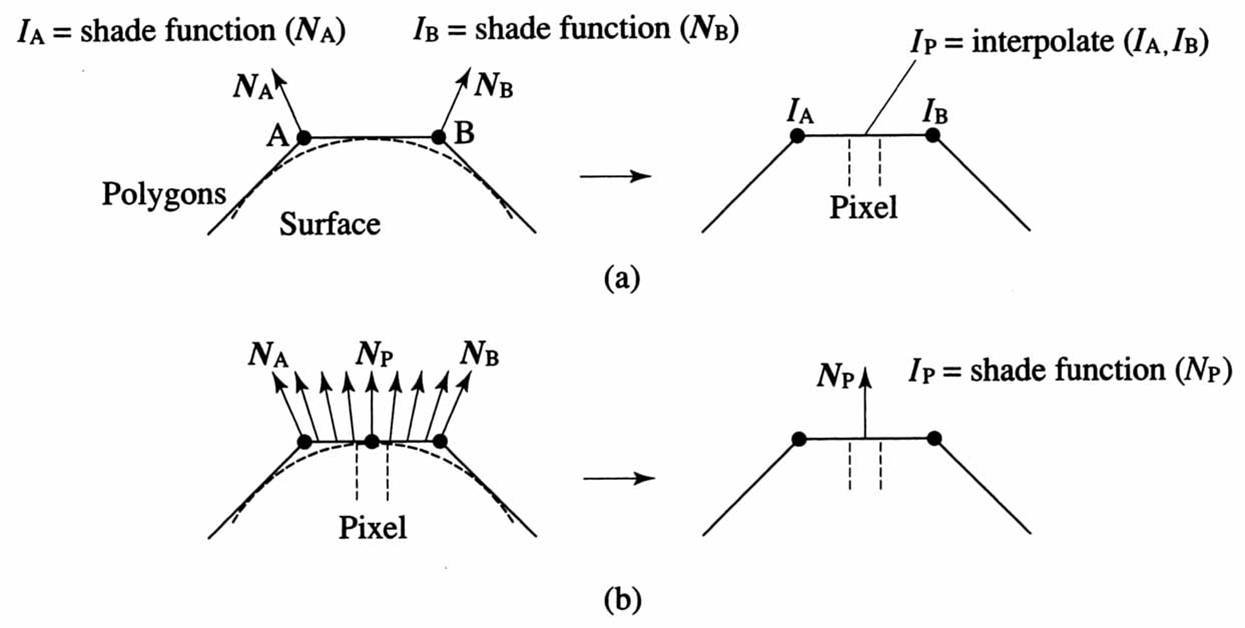
本文转自:博客园 - qingsun_ny,转载此文目的在于传递更多信息,版权归原作者所有。


