作者：刘建平Pinard
贝叶斯个性化排序(Bayesian Personalized Ranking, 以下简称BPR)，它也用到了矩阵分解，但是和funkSVD家族却有很多不同之处。下面我们来详细讨论。
1. BPR算法使用背景
在很多推荐场景中，我们都是基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，这是funkSVD之类算法的做法，使用起来也很有效。但是在有些推荐场景中，我们是为了在千万级别的商品中推荐个位数的商品给用户，此时，我们更关心的是用户来说，哪些极少数商品在用户心中有更高的优先级，也就是排序更靠前。也就是说，我们需要一个排序算法，这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的排序算法。
2. 排序推荐算法背景介绍
排序推荐算法历史很悠久，早在做信息检索的各种产品中就已经在使用了。最早的第一类排序算法类别是点对方法(Pointwise Approach)，这类算法将排序问题被转化为分类、回归之类的问题，并使用现有分类、回归等方法进行实现。第二类排序算法是成对方法(Pairwise Approach)，在序列方法中，排序被转化为对序列分类或对序列回归。所谓的pair就是成对的排序，比如(a,b)一组表明a比b排的靠前。我们要讲到的BPR就属于这一类。第三类排序算法是列表方法(Listwise Approach)，它采用更加直接的方法对排序问题进行了处理。它在学习和预测过程中都将排序列表作为一个样本。排序的组结构被保持。
本文关注BPR，这里我们对排序推荐算法本身不多讲，如果大家感兴趣，可以阅读李航的A Short Introduction to Learning to Rank.
http://times.cs.uiuc.edu/course/598f13/l2r.pdf
3. BPR建模思路
在BPR算法中，我们将任意用户 u 对应的物品进行标记，如果用户 u 在同时有物品 i 和 j 的时候点击了 i ，那么我们就得到了一个三元组 < u , i , j > ，它表示对用户 u 来说，i 的排序要比 j 靠前。如果对于用户 u 来说我们有 m 组这样的反馈，那么我们就可以得到 m 组用户 u 对应的训练样本。
既然是基于贝叶斯，那么我们也就有假设，这里的假设有两个：一是每个用户之间的偏好行为相互独立，即用户 u 在商品 i 和 j 之间的偏好和其他用户无关。二是同一用户对不同物品的偏序相互独立，也就是用户 u 在商品 i 和 j 之间的偏好和其他的商品无关。为了便于表述，我们用 >u 符号表示用户 u 的偏好，上面的 < u , i , j > 可以表示为：i >u j 。
在BPR中，这个排序关系符号 >u 满足完全性，反对称性和传递性，即对于用户集 U 和物品集 I ：
同时，BPR也用了和funkSVD类似的矩阵分解模型，这里BPR对于用户集U和物品集I的对应的 U× I 的预测排序矩阵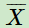
，我们期望得到两个分解后的用户矩阵 W ( |U| × k ) 和物品矩阵 H( |I| × k )，满足
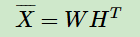
这里的k和funkSVD类似，也是自己定义的，一般远远小于 |U| , |I| 。
由于BPR是基于用户维度的，所以对于任意一个用户 u ，对应的任意一个物品 i 我们期望有：
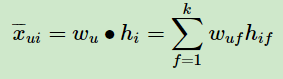
最终我们的目标，是希望寻找合适的矩阵 W , H，让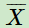和 X 最相似。读到这里，也许你会说，这和funkSVD之类的矩阵分解模型没有什么区别啊？ 的确，现在还看不出，下面我们来看看BPR的算法优化思路，就会慢慢理解和funkSVD有什么不同了。
4. BPR的算法优化思路
BPR 基于最大后验估计 P ( W , H| >u )来求解模型参数 W , H , 这里我们用 θ 来表示参数W和 H, >u 代表用户 u 对应的所有商品的全序关系，则优化目标是 P ( θ | >u )。根据贝叶斯公式，我们有：
由于我们求解假设了用户的排序和其他用户无关，那么对于任意一个用户u来说，P( >u )对所有的物品一样，所以有：
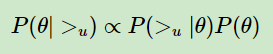
这个优化目标转化为两部分。第一部分和样本数据集D有关，第二部分和样本数据集D无关。
对于第一部分，由于我们假设每个用户之间的偏好行为相互独立，同一用户对不同物品的偏序相互独立，所以有：
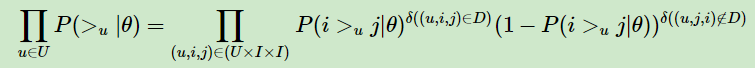
其中，
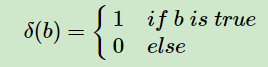
根据上面讲到的完整性和反对称性，优化目标的第一部分可以简化为：
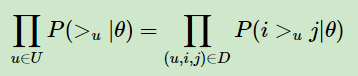
而对于P ( i >u j |θ ) 这个概率，我们可以使用下面这个式子来代替：
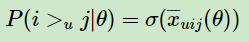
其中，σ(x)是sigmoid函数。这里你也许会问，为什么可以用这个sigmoid函数来代替呢? 其实这里的代替可以选择其他的函数，不过式子需要满足BPR的完整性，反对称性和传递性。原论文作者这么做除了是满足这三个性质外，另一个原因是为了方便优化计算。
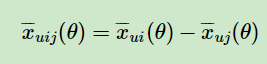
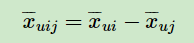
注意上面的这个式子也不是唯一的，只要可以满足上面提到的当 i >u j 时，
，以及对应的相反条件即可。这里我们仍然按原论文的式子来。
最终，我们的第一部分优化目标转化为：
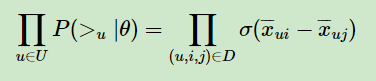
对于第二部分P(θ)，原作者大胆使用了贝叶斯假设，即这个概率分布符合正太分布，且对应的均值是0，协方差矩阵是 λ θ I ,即
原作者为什么这么假设呢？个人觉得还是为了优化方便，因为后面我们做优化时，需要计算lnP( θ )，而对于上面假设的这个多维正态分布，其对数和 ||θ||2 成正比。即：
最终对于我们的最大对数后验估计函数
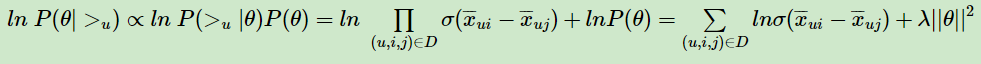
这个式子可以用梯度上升法或者牛顿法等方法来优化求解模型参数。如果用梯度上升法，对θ求导，我们有：
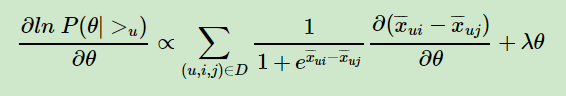
由于
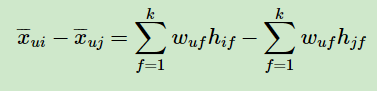
这样我们可以求出：
有了梯度迭代式子，用梯度上升法求解模型参数就容易了。下面我们归纳下BPR的算法流程。
5. BPR算法流程
下面简要总结下BPR的算法训练流程：
输入：训练集D三元组，梯度步长 α ， 正则化参数 λ , 分解矩阵维度 k 。
输出：模型参数，矩阵 W , H
1. 随机初始化矩阵 W , H
2. 迭代更新模型参数：
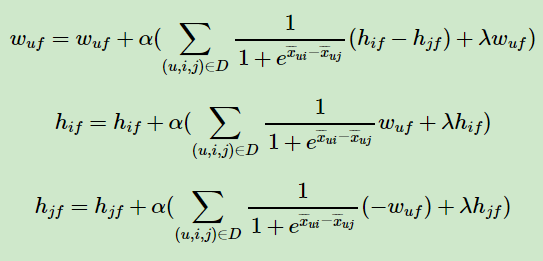
3. 如果 W , H 收敛，则算法结束，输出 W , H ，否则回到步骤 2 .
当我们拿到 W , H 后，就可以计算出每一个用户 u 对应的任意一个商品的排序分：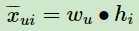
，最终选择排序分最高的若干商品输出。
6. BPR小结
BPR是基于矩阵分解的一种排序算法，但是和funkSVD之类的算法比，它不是做全局的评分优化，而是针对每一个用户自己的商品喜好分贝做排序优化。因此在迭代优化的思路上完全不同。同时对于训练集的要求也是不一样的，funkSVD只需要用户物品对应评分数据二元组做训练集，而BPR则需要用户对商品的喜好排序三元组做训练集。
在实际产品中，BPR之类的推荐排序在海量数据中选择极少量数据做推荐的时候有优势，因此在某宝某东等大厂中应用也很广泛。
（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）
本文转自：博客园 - 刘建平Pinard，转载此文目的在于传递更多信息，版权归原作者所有。
