概述
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。
朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法简单。理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。
定义
贝叶斯方法
贝叶斯方法是以贝叶斯原理为基础,使用概率统计的知识对样本数据集进行分类。由于其有着坚实的数学基础,贝叶斯分类算法的误判率是很低的。贝叶斯方法的特点是结合先验概率和后验概率,即避免了只使用先验概率的主观偏见,也避免了单独使用样本信息的过拟合现象。贝叶斯分类算法在数据集较大的情况下表现出较高的准确率,同时算法本身也比较简单。
朴素贝叶斯算法
朴素贝叶斯算法(Naive Bayesian algorithm) 是应用最为广泛的分类算法之一。
朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化,即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重,也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。
算法原理
朴素贝叶斯分类(NBC)是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法,先通过已给定的训练集,以特征词之间独立作为前提假设,学习从输入到输出的联合概率分布,再基于学习到的模型,输入X求出使得后验概率最大的输出Y。
设有样本数据集
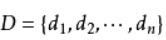
对应样本数据的特征属性集为
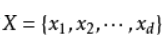
类变量为
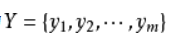
即D可以分为ym类别。其中
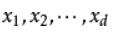
相互独立且随机,则Y的先验概率Pprior = P(Y),Y的后验概率Ppost = P(Y|X),由朴素贝叶斯算法可得,后验概率可以由先验概率Pprior = P(Y)、证据P(X)、类条件概率P(X|Y)计算出:
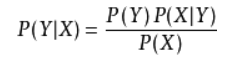
朴素贝叶斯基于各特征之间相互独立,在给定类别为y的情况下,上式可以进一步表示为下式:
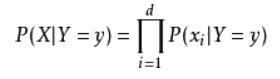
由以上两式可以计算出后验概率为:
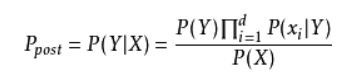
由于*P(X)*的大小是固定不变的,因此在比较后验概率时,只比较上式的分子部分即可。因此可以得到一个样本数据属于类别yi的朴素贝叶斯计算如下图所示:
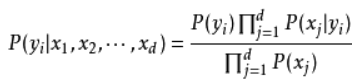
优缺点
优点
朴素贝叶斯算法假设了数据集属性之间是相互独立的,因此算法的逻辑性十分简单,并且算法较为稳定,当数据呈现不同的特点时,朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好,对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时,朴素贝叶斯分类算法会有较好的效果。
缺点
属性独立性的条件同时也是朴素贝叶斯分类器的不足之处。数据集属性的独立性在很多情况下是很难满足的,因为数据集的属性之间往往都存在着相互关联,如果在分类过程中出现这种问题,会导致分类的效果大大降低。
应用
文本分类
分类是数据分析和机器学习领域的一个基本问题。文本分类已广泛应用于网络信息过滤、信息检索和信息推荐等多个方面。数据驱动分类器学习一直是近年来的热点,方法很多,比如神经网络、决策树、支持向量机、朴素贝叶斯等。相对于其他精心设计的更复杂的分类算法,朴素贝叶斯分类算法是学习效率和分类效果较好的分类器之一。直观的文本分类算法,也是最简单的贝叶斯分类器,具有很好的可解释性,朴素贝叶斯算法特点是假设所有特征的出现相互独立互不影响,每一特征同等重要。但事实上这个假设在现实世界中并不成立:首先,相邻的两个词之间的必然联系,不能独立;其次,对一篇文章来说,其中的某一些代表词就确定它的主题,不需要通读整篇文章、查看所有词。所以需要采用合适的方法进行特征选择,这样朴素贝叶斯分类器才能达到更高的分类效率。
其他
朴素贝叶斯算法在文字识别, 图像识别方向有着较为重要的作用。 可以将未知的一种文字或图像,根据其已有的分类规则来进行分类,最终达到分类的目的。
现实生活中朴素贝叶斯算法应用广泛,如文本分类,垃圾邮件的分类,信用评估,钓鱼网站检测等等。
本文转自:CSDN - 是DRR啊,转载此文目的在于传递更多信息,版权归原作者所有。






