机器学习之支持向量机算法(一)

一、问题引入

支持向量机(SVM，Support Vector Machine)在2012年前还是很牛逼的，但是在12年之后神经网络更牛逼些，但是由于应用场景以及应用算法的不同，我们还是很有必要了解SVM的，而且在面试的过程中SVM一般都会问到。支持向量机是一个非常经典且高效的分类模型。我们的目标：基于下述问题对SVM进行推导。

要解决的问题：如下图所示，3条黑色的线都可以将两边的数据进行分类，那哪条线作为决策边界才是最好的呢？如果特征数据本身就很难分，那又怎么办呢？计算复杂度怎么样？能实际应用吗？

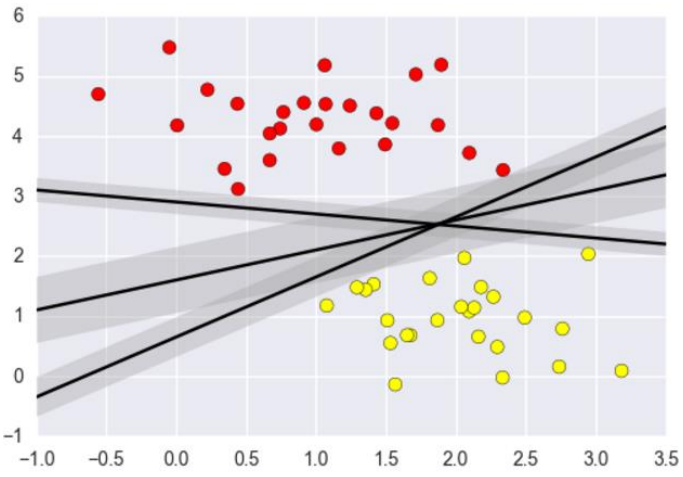
二、距离求解

假设有一个部队过雷区，左边是一堆雷区，右边是另一堆雷区，现在需要开辟出部队前进的方向。我们需要做的就是让这个方向完全分割开左边和右边的雷区，并且我们肯定希望这个方向的边界越大越好，这样踩雷的风险就越低。

决策边界：选出来离雷区最远的（雷区就是边界上的点，要Large Margin(间隔)），毫无疑问第二个分类效果肯定比第一个好。那为什么需要这个边界距离越大越好呢？答案就是边界越大在测试集上的泛化能力就越好。

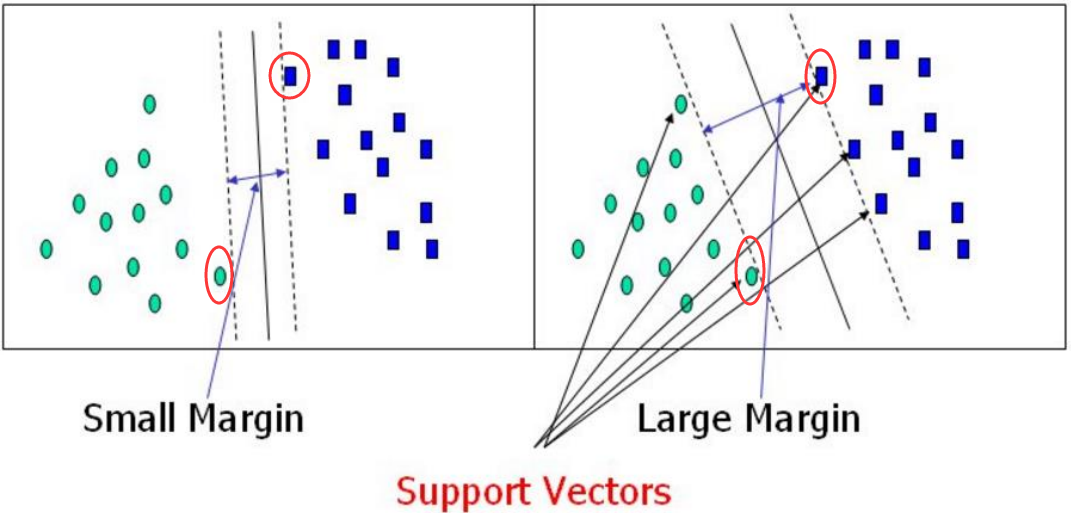
我们如果说找到了离决策边界最近的点，那这样就找到了决策边界，如上面圈出来的这些点。所以我们现在需要计算出到底哪个点距离决策边界最近吧，在这之前，首先需要引入这个距离是怎么计算的。

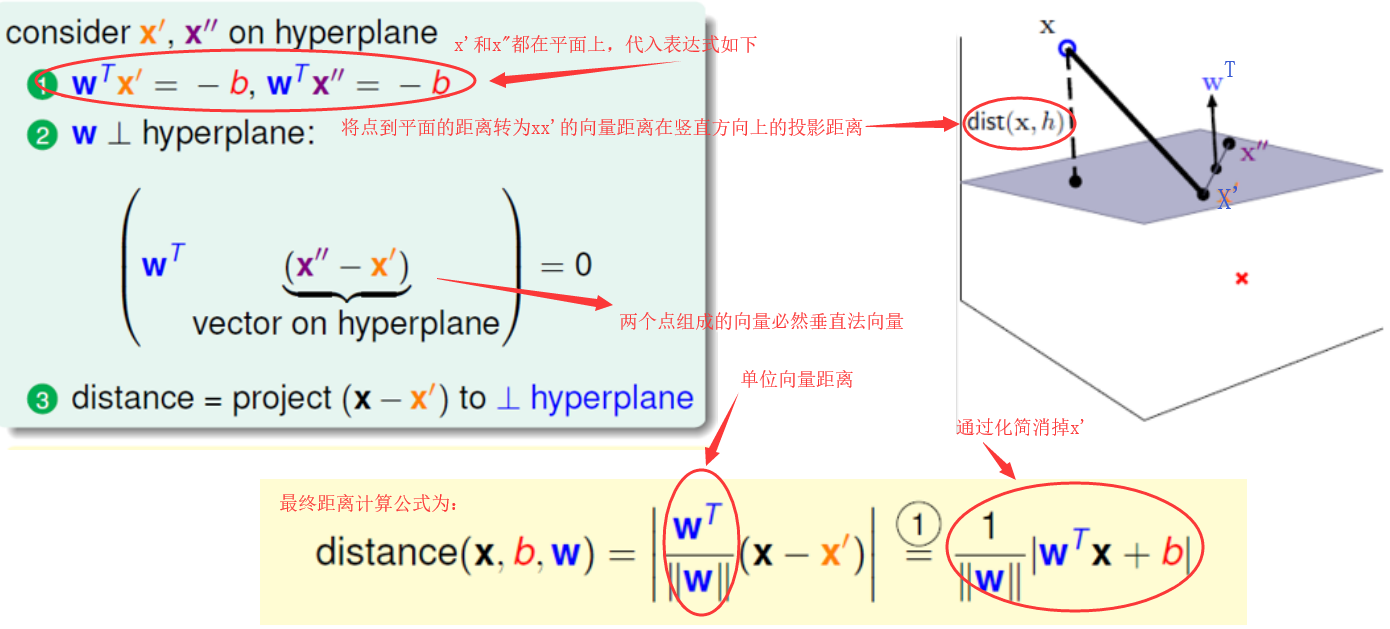
首先，我们假设决策边界是一个阴影平面，那这个距离就是求点到平面的距离，然后将这个距离转换成求点到点的距离，然后再求出这个点到点的距离在垂直于这个平面上的投影，那么这个投影就是点到平面的距离了。

那接下来，我们可以假设这个平面方程为 w^Tx + b = 0 。初学的我好像并不明白这个方程怎么来的，后来查阅一些资料得知。

因为二维空间里面，一条直线的方程可以表示为：Ax+By+C=0。三维空间里面，平面的方程可以表示为：Ax + By + Cz + D = 0。依次推广，n维空间的超平面方程可以表示为：Ax₁ + Bx₂ + Cx₃ + Dx₄ + Ex₅ + Fx₆ + .... + K = 0

因为n维空间对应的是 n 维坐标系，仅仅用 x、y、z 几个字母较难表示，所以此处用x₁、x₂、x₃、...、x_n 来表示 n 维坐标系，各个维度的系数此处也可以用 w₁、w₂、w₃、...、w_n 来表示，所以 n 维空间里面的超平面方程可以写成如下形式：w₁x₁+ w₂x₂ + w₃x₃+w₄x₄ + ... + w_nx_n + b = 0。

wx 相乘可以看作是内积的相乘：

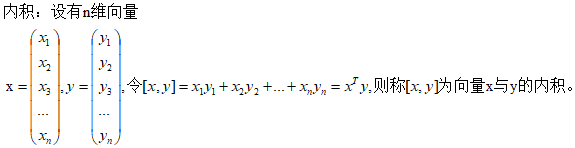
可以将 x 看作 w，y 看作 x 则上面超平面方程就变成了：[w,x] + b = 0 ，即 w^Tx + b = 0 。所以，样本空间中，任何一个超平面都可以用方程如下方程表示：W^TX + b = 0。其中，W = ( w₁, w₂, w₃, ..., w_n ) 为法向量，b为位移项可以认为是截距，该超平面可以唯一的由此方程决定。

三、目标函数

上面已经得出了距离的计算公式，那现在就要依据这个距离公式来找出最优的决策边界了。首先假设平面上有三个数据点 ( X₁ , Y₁ )( X₂ , Y₂ ) … ( X_n , Y_n )，注意这里 X 和 Y 不是代表横纵坐标，X 代表数据的样本，Y 为样本的类别也就是样本标签。现在使用支持向量机做一个二分类问题，也就是说如果当X为正例时那么 Y = +1，当X为负例时 Y = -1。

现在决策边界方程为：y( x ) = w^TΦ(x) + b（其中Φ(x)是对数据做了核变换，后面继续说）。根据上面所述可以得到如下图所示的表达式。

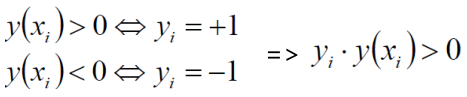
我们最终需要得到的决策边界，通俗解释就是，找到一个条线（w和b），使得离该线最近的点（雷区）离这条线的距离能够最远，那这条线就是我们的决策边界了。这句话很重要，建议读者认真多读几遍。

上面最终得出距离公式为：

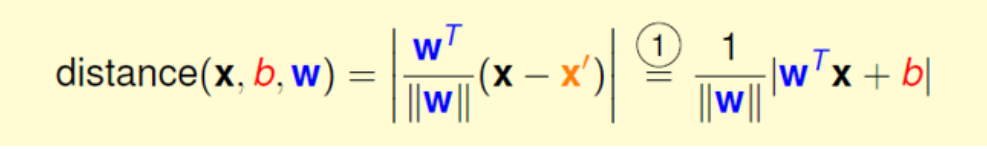
这里的 w^Tx + b 就是我们的决策方程 y( x_i )，这里我们需要去掉外面的这个绝对值符号，而根据上面这个表达式 y_i * y( x_i ) > 0，经过化简可以得出以下的一个距离的表达式 ( 由于 y_i * y( x_i ) > 0 所以将绝对值展开原式依旧成立)：

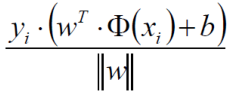
现在得到了这个问题中的距离公式，而现在我们的目标就是找出使这个函数的值最小但是两个参数(w,b)值却最大。如下式所示，min就是找到离决策边界最近的那个样本点，max就是找出w和b使最近的样本点到决策边界那条线的距离最远。

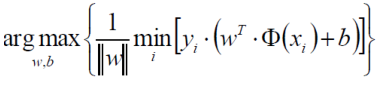
上面的式子似乎太长了些，我们可以通过放缩变换来简化一下这个式子。对于决策方程（w，b）我们总可以通过一种放缩手段(比如同时乘以或者除以一个值)来使得其结果值 |Y| >= 1，于是可以推导出 y_i * ( w^TΦ( x_i ) + b ) > = 1（之前我们认为恒大于 0，现在严格了些）。由于 y_i * (w^TΦ( x_i ) + b) > = 1，也就是说 y_i * (w^TΦ( x_i ) + b ) 的最小值就是 1，那现在只需考虑下面这个式子就足够了。

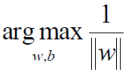
那这个函数就是最终的一个目标函数，也就是说需要求解出什么样的一个 w 来使得最终结果值越大越好。对于当前目标，我们需要求出一个极大值，注意当前约束条件 y_i * ( w^TΦ( x_i ) + b ) > = 1

常规套路就是将求解极大值问题转换为极小值问题 = > minw,b(1/2 * w2)，求 1/w 的最大值，相当于求w的最小值，也相当于求 w2（消除掉绝对值的影响）的最小值，那为啥需要引入一个常数 1/2 呢，这是为了后面方便进行求导。如何求解，应用拉格朗日乘子法求解，拉格朗日主要解决的带约束的优化问题

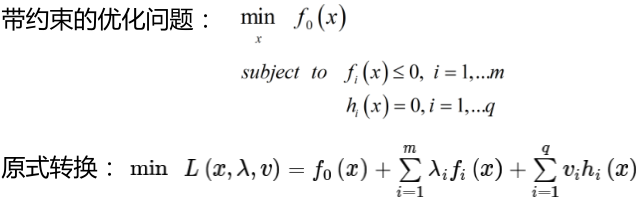
这个式子有点复杂，大概意思就是说在直接求带约束的优化问题的时候不太好求，那就需要转换一下，将我们需要求的变量转换为求一个中间变量的解，然后再找出这个中间变量的解与我们需要求解的变量之间的关系，这样就可以通过这个中间变量求出我们需要求解的变量。

依照上式再将我们的需要求解的式子转换为 ：（约束条件不要忘 y_i * ( w^TΦ( x_i ) + b ) > = 1）这里多了一个参数 α

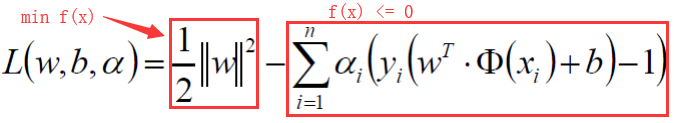
四、SVM求解

分别对w和b求偏导，分别得到两个条件（由于拉格朗日中的对偶性质KKT）

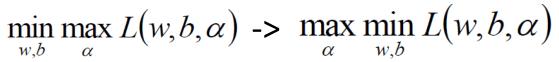
大概意思就是说在拉格朗日乘子法中先求解最大值然后求解最小值这个过程可以转换成先求解成最小值再求解成最大值。在这儿我们先求解这个函数的极小值， 首先在L(w,b,α)函数中对w，b分别求偏导，由于需要求解极值点，令其偏导等于0。

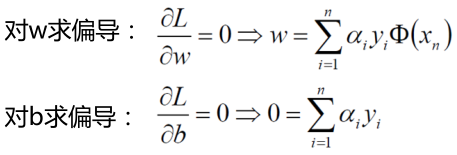
可以看出 w 与 α 这个变量有了关系，就是说求出 α 也就求出了 w 。 然后继续接下来的求解，将上面求出的两个式子带回原式。

然后接下来求解 α 的极大值

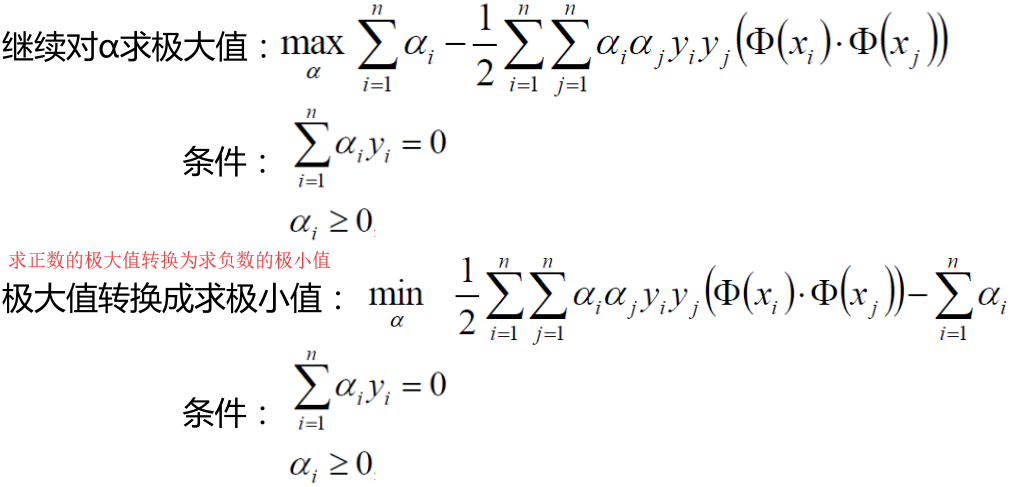
未完待续。。。

本文转自：博客园 - |旧市拾荒|，转载此文目的在于传递更多信息，版权归原作者所有。