特征分解和奇异值分解

特征分解和奇异值分解在机器学习的应用中经常出现，在学习线性代数的时候也学习过。线性代数学完之后，之后去按照步骤去求解特征值和特征向量，也没搞明白特征值和特征向量究竟有什么作用。

这篇文章的主要内容包括：
1、什么是特征分解
2、什么是奇异值分解
3、如何求解特征值和特征向量
4、特征值和特征向量有什么意义

一、特征分解

特征分解(eigendecomposition)：是使用最广的矩阵分解之一，通过特征分解可以将矩阵分解成一组特征值和特征向量。方阵A的特征向量(eigenvector)是指与A相乘后相当于对该向量进行缩放的非零向量v

其中v就是方阵A的特征向量，λ就是A的特征值。如果v是A的特征向量，那么任何缩放后的向量s*v(s为任意实数，且不为0)也是A的特征向量。同时sv和v具有相同的特征值。所以，通常情况下我们都只考虑单位特征向量。通过将矩阵分解成为特征值和特征向量，来帮助我们分析矩阵。

二、奇异值分解

奇异值分解(singular value decomposition,SVD)：是将矩阵分解成为特征值和特征向量的另一种方法，通过奇异值分解，可以将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。通过奇异值分解，我们可以得到一些与特征分解相同类型的信息。而且，奇异值分解的应用非常广泛，如推荐系统、图片压缩等。每一个实数矩阵都有一个奇异值分解，但不一定有特征分解。非方阵的矩阵没有特征分解，此时我们只能使用奇异值分解。

奇异值分解，可以将矩阵A分成三个矩阵的乘积：

假设A是一个m×n的矩阵，那么U是一个m×m的矩阵，D是一个m×n的矩阵，V是一个n×n的矩阵。其中，矩阵U和V都是正交矩阵，而矩阵D是对角矩阵。矩阵D不一定是方阵。

对角矩阵D对角线上的元素就是矩阵A的奇异值(singular value)。矩阵U的列向量是左奇异向量(left singular vector)，矩阵V的列向量是右奇异向量(right singular vector)。

我们可以通过特征分解来解释奇异值分解，A的左奇异向量是A乘A的转置的特征向量，A的右奇异向量是A的转置乘A的特征向量。A的非零奇异值是A的转置乘A特征值的平方根，也是A乘A的转置特征值的平方根。

三、特征值和特征向量的求解

在线性代数中，有介绍过通过矩阵的运算来求解矩阵的特征值和特征向量，下面通过一个例子来介绍一下整个运算过程

下面我们通过numpy来对求解矩阵A的特征值和特征向量

import numpy as np
 
if __name__ == "__main__":
    #定义一个矩阵
    a_matrix = np.array([[4,6,0],[-3,-5,0],[-3,-6,1]])
    #求特征值和特征向量
    egien_vals,egien_vec = np.linalg.eig(a_matrix)
    #获取特征值
    print(egien_vals)
    #获取特征向量
    print(egien_vec)

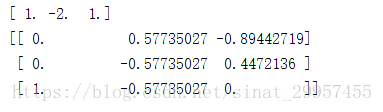
通过对比可以发现，使用numpy求出来的特征向量好像与我们所求的有些不一样，那是因为numpy将特征向量进行了归一化。

四、特征值和特征向量的含义

其实在将矩阵分解成为特征值和特征向量的时候，在PCA和LDA中都有应用。我们将矩阵分解之后，按照特征值的大小对对应的特征向量进行排序，然后根据我们需要将原始矩阵降低到指定的维度，取前k个特征向量，组合成为一个映射矩阵，然后通过映射矩阵将原始矩阵映射到降维后的空间中。

其实，我们可以将矩阵的分解过程理解为一个力的分解，其中特征向量代表了分解力的方向，特征值代表分解的力在这个方向上的大小，我们也可以通过分解的力来得到合成力(矩阵)。在使用奇异值压缩图片的时候，正是使用了这一思想。

版权声明：本文为CSDN博主「修炼之路」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/sinat_29957455/article/details/80206589