本文主要介绍一个被广泛使用的机器学习分类算法,K-nearest neighbors(KNN),中文叫K近邻算法。

KNN
k近邻算法是一种基本分类和回归方法。
KNN实际上也可以用于回归问题,不过在工业界使用得比较广泛的还是分类问题
KNN的核心思想也非常简单,如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,比如下图,当K=3时,节点会被预测属于红色椭圆类。有点“近朱者赤,近墨者黑”的感觉。
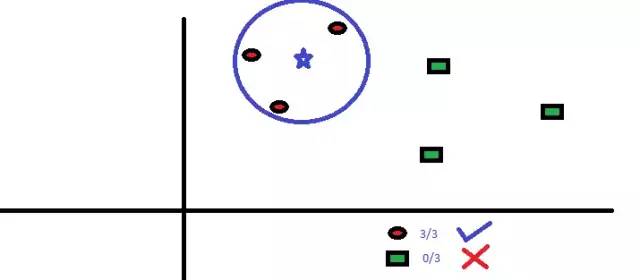
算法的原理非常简单,但这其中隐藏了一些值得被探讨的点:
• k该如何取值?
• 距离最近中的“距离”是什么,怎么计算会更好?
• 如果对于一个数据要计算它与模型中所有点的距离,那当数据量很大的时候性能会很差,怎么改善?
• 在一些情况下明明数据离某一个点特别近,但有另外两个同类的点离得很远但被K包含在内了,这种情况把数据划为这两个点的同类是不是不太合理?
• 如果训练数据不均衡(Imbalance data)怎么办?
• 特征的纬度量纲跨越很大(比如10和10000)怎么办?
• 特征中含有类型(颜色:红黄蓝绿)怎么处理?
下面我们一一来解决与KNN相关的一些问题
超参数(Hyperparameter)K的选取
超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。比如:
• 训练神经网络的学习速率。
• 学习速率
• 用于支持向量机的C和sigma超参数。
• K最近邻的K。
KNN中,K越大则类与类的分界会越平缓,K越小则会越陡峭。当K越小时整个模型的错误率(Error Rate)会越低(当然过拟合的可能就越大)。
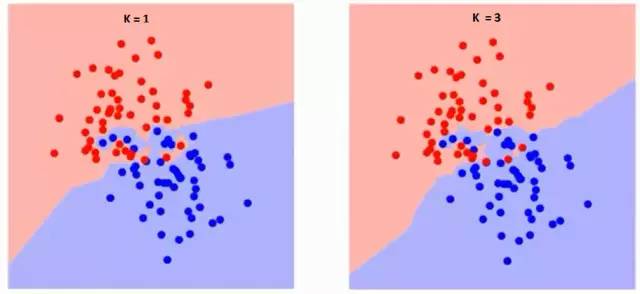
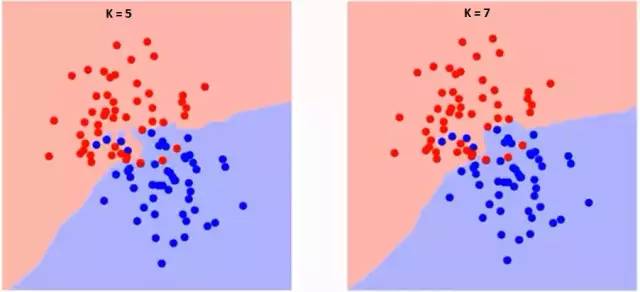
由于KNN一般用于分类,所以K一般是奇数才方便投票
一般情况下,K与模型的validation error(模型应用于验证数据的错误)的关系如下图所示。
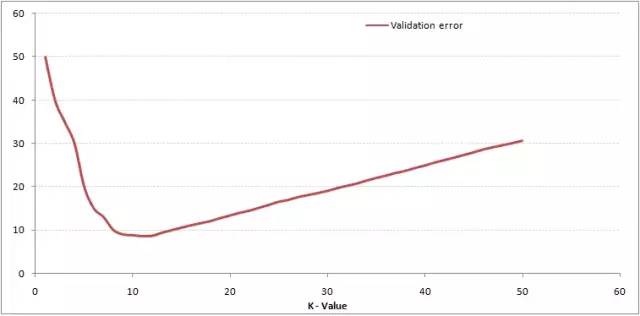
K越小则模型越过拟合,在验证数据上表现肯定一般,而如果K很大则对某个数据的预测会把很多距离较远的数据也放入预测,导致预测发生错误。所以我们需要针对某一个问题选择一个最合适的K值,来保证模型的效果最好。本文仅介绍一种“交叉验证法”,
交叉验证法(Cross Validation)
在机器学习里,通常来说我们不能将全部用于数据训练模型,否则我们将没有数据集对该模型进行验证,从而评估我们的模型的预测效果。为了解决这一问题,有如下常用的方法:
• The Validation Set Approach
• Cross-Validation
The Validation Set Approach指的是最简单的,也是很容易就想到的。我们可以把整个数据集分成两部分,一部分用于训练,一部分用于验证,这也就是我们经常提到的训练集(training set)和验证集(Validation set)

然而我们都知道,当用于模型训练的数据量越大时,训练出来的模型通常效果会越好。所以训练集和测试集的划分意味着我们无法充分利用我们手头已有的数据,所以得到的模型效果也会受到一定的影响。
基于这样的背景有人就提出了交叉验证法(Cross-Validation)。
这里简单介绍下k-fold cross-validation,指的是将所有训练数据折成k份,如下图是当折数k=5时的情况。

我们分别使用这5组训练-验证数据得到KNN超参数K为某个值的时候,比如K=1的5个准确率,然后将其准确率取平均数得到超参数K为1时的准确率。然后我们继续去计算K=3 K=5 K=7时的准确率,然后我们就能选择到一个准确率最高的超参K了。
KNN中的距离
K近邻算法的核心在于找到实例点的邻居,那么邻居的判定标准是什么,用什么来度量?这在机器学习领域其实就是去找两个特征向量的相似性。机器学习中描述两个特征向量间相似性的距离公式有很多:
欧氏距离
常见的两点之间或多点之间的距离表示法
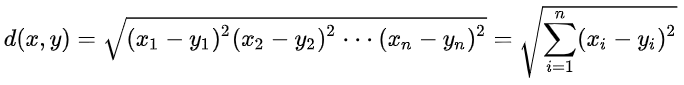
曼哈顿距离
曼哈顿距离指的是在向量在各坐标轴上投影的距离总和,想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”,此即曼哈顿距离名称的来源, 同时,曼哈顿距离也称为城市街区距离(City Block distance)。
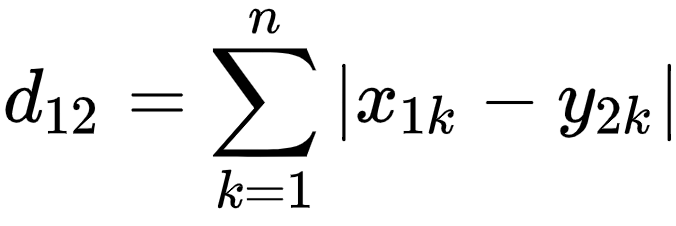
马氏距离(Mahalanobis Distance)
由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出,表示数据的协方差距离。是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离。
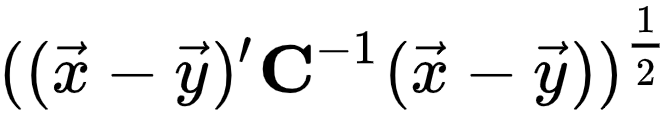
其他
• 切比雪夫距离(Chebyshev distance)
• 闵可夫斯基距离(Minkowski Distance)
• 标准化欧氏距离 (Standardized Euclidean distance )
• 巴氏距离(Bhattacharyya Distance)
• 汉明距离(Hamming distance)
• 夹角余弦(Cosine)
• 杰卡德相似系数(Jaccard similarity coefficient)
• 皮尔逊系数(Pearson Correlation Coefficient)
大数据性能优化
从原理中很容易知道,最基本的KNN算法的时间复杂度是O(N),因为对于某一个数据,必须计算它必须与模型中的所有点的距离。有没有办法优化这部分性能呢?这里主要说下两个方法。
K-d tree
K-d trees are a wonderful invention that enable O( klogn) (expected) lookup times for the k nearest points to some point x. This is extremely useful, especially in cases where an O(n) lookup time is intractable already.
其算法的核心思想是分而治之,即将整个空间划分为几个小部分。
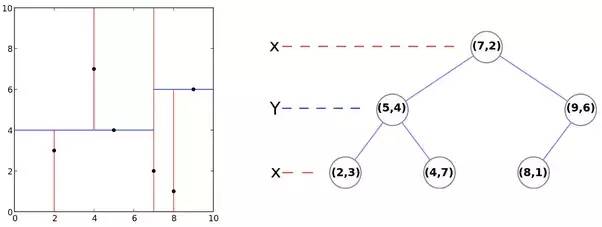
注意K-D树对于数据纬度d来说是指数级的复杂度,所以只适合用在数据纬度较小的情况。
Locality Sensitivity Hasing(LSH)

LSH的基本思想是将数据节点插入Buckets,让距离近的节点大概率插入同一个bucket中,数据间距离远的两个点则大概率在不同的bucket,这使得确定某点最临近的节点变得更为容易。
所以LSH不能保证一定准确
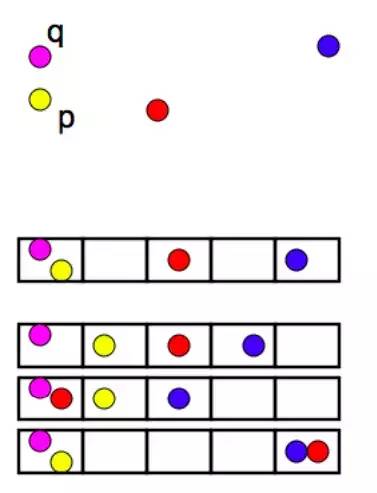
样本的重要性
在一些情况下明明数据离某一个点特别近,但有另外两个同类的点离得很远但被K包含在内了,这种情况把数据划为这两个点的同类是不是不太合理。
例如下图,当K=3时,红点会被投票选举成Offer类,但实际上这个点可能更加适合分类为No Offer。
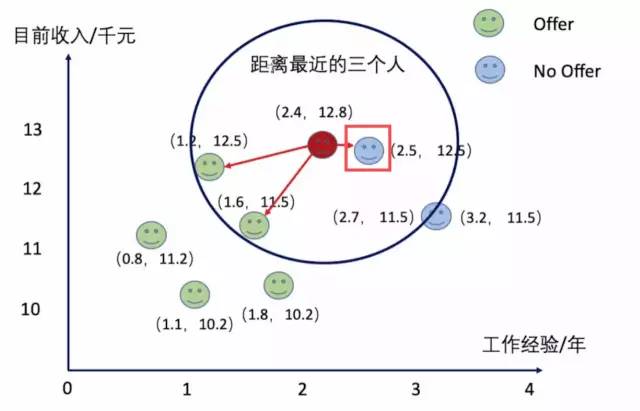
为了解决这一问题有一种方法Distance-weighted nearest neighbor,其核心思想是让距离近的点可以得到更大的权重。
本文转自:君君ei,作者:star,转载此文目的在于传递更多信息,版权归原作者所有。