模型集成方法
集成学习(ensemble learning)是机器学习中一类学习算法,值训练多个学习器并将它们组合起来使用的方法。这类算法通常在实践中会取得比单个学习器更好的预测结果。
数据层面的集成方法
在训练阶段的数据扩充在测试阶段仍然使用。 诸如图像多尺度, 随机扣取等。以随机扣取为例, 对某张测试图片可得到n 张随机扣取图像,测试阶段只需要用训练好的深度网络模型对n张图分别做预测, 之后将预测的各类置信度平均作为该测试图像最终预测结果即可。
简易集成法
简易集成法是Liu 等人提出的针对不平衡样本问题的一种集成学习解决方案, 具体来说,简易集成法对于样本较多的类采取降采样,每次采样数根据样本数目最少的类别而定,这样,每类取到的样本数可保持均等。 采样结束后, 针对每次采样得到的子数据集训练模型, 如此采样, 训练,反复多次。最后, 对测试数据的预测则根据训练得到若干模型的结果取平均值或投票得出。 总结, 简易集成法在模型集成的同时,还能缓解数据不平衡带来的问题。
模型层面的集成方法
单模型集成
多层特征融合
多层特征融合是针对单模型的一种模型层面的集成方法。 由于深度卷积神经网络特征具有层次性的特点, 不同层特征富含的语义信息可以相互补充, 在图像语义分割, 细粒度图像检索,基于视频的表象性格分析等任务中常见的多层特征融合策略的使用。一般的,多层特征融合操作时可将不同层网络特征级联。而对于特征融合应选取哪些网络层,一个实践经验是:最好使用靠近目标函数的几层卷积特征。因为越深层特征包含的高层语义越强,分辨力也会越强。相反, 网络较浅层的特征较普使, 用于特征融合可能起不到作用,或者甚至会起到相反作用。
网络快照集成法 (snapshot ensemble)
深度神经网络模型复杂的解空间存在非常多的局部最优解, 但经典的随机梯度下降方法只能让网络模型收敛到其中一个局部最优解。 网络快照便利用了网络解空间中这些局部最优解来对单个网络做模型集成。 通过循环调整网络的学习率可使网络依次收敛到不同的局部最优解。

最左侧图为传统SGD法, 中间为快照集成法的收敛示意图。 右图为两方法在CIFAR-10数据集上的收敛曲线对比。
具体而言, 网络快照法是将学习率η设置为随模型迭代轮数 t(iteration,即一次批处理随机梯度下降称为一个迭代轮数)改变的函数,即:

其中,η0 为初始学习率, 一般设置为0.1, 0.2 。t 为模型迭代轮数(即mini-batch批处理训练次数)。T 为模型总的批处理训练次数。 M为学习率“循环退火”的次数。 对应了模型将收敛到的局部最优解的个数。 式子用cos 的循环性来更新学习率, 将学习率从0.1 随 t 的增长逐渐减缓到0, 之后学习率重新放大而跳出局部最优解。自此开始下一个循环,此循环结束可以收敛到新的局部最优解, 如此循环往复……直到M个循环结束。 上面用余弦函数循环更新网络参数,这一过程称之为“循环余弦退火”过程。
当经过循环余弦退火对学习率的调整之后, 每个循环结束可使模型收敛到一个不同的局部最优解, 若将收敛到不同局部最优解的模型保存便可得到M个处于不同收敛状态的模型,对于每个循环结束后保存的模型,我们称之为模型快照。 测试阶段在做模型集成时,由于深度网络模型在初始训练阶段未必有比较卓越的性能,因此一般可挑选最后m个模型快照用于集成。
关于这些模型快照的集成策略参考下面提到的“直接平均法”。
多模型集成
多模型生成策略
① 同一模型不同的初始化: 由于神经网络的训练机制是基于随机梯度下降, 故不同的网络参数初始化会导致不同的训练结果,尤其是对于小样本的学习场景, 首先对同一模型进行不同初始化,之后得到的网络模型进行结果集成会大幅度缓解其随机性,提升最终任务的预测结果。
② 若网络超参数设置得当, 深度模型随着网络的进行会逐步趋于收敛,但是不同的训练轮数仍有不同, 无法确定哪一轮的模型最适合用于测试数据。 一个简单方法解决这个问题是将最后几轮参数模型结果做集成, 这样一方面可以降低随机误差,另一方面可以避免训练轮此过多带来的过拟合现象, 这样的操作被称为轮次集成。
③ 不同目标函数:目标函数(或称损失函数)是整个网络训练的“指挥棒”, 选择将“交叉熵损失函数”、“合页损失函数”、“大间隔交叉熵损失函数”和“中心损失函数”作为目标函数分别训练模型。在预测阶段,既可以直接对不同模型预测结果做“置信度级别”的平均或投票,也可以做“特征级别”的模型集成:将不同网络得到的深度特征抽出后级联作为最终特征,之后离线训练浅层分类器(如支持向量机)完成预测任务。
④ 不同的网络结构:可以在使用如VGG, 深度残差等不同网络架构的网络上训练模型,最后将不同架构网络得到的结果做集成。
多模型集成方法
假设由 N 个模型待集成, 对某测试样本 x , 其预测结果为 N 个 C 维向量( C 为数据的标记空间大小):s1,s2,...,sN
直接平均法
直接平均法是最简单有效的多模型集成方法,通过直接平均不同模型产生的类别置信度得到最后额预测结果

加权平均法
加权平均法是直接平均的基础上加入权重来调节不同模型输出间的重要程度。
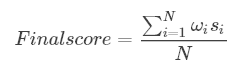
其中 ωi 为第i个模型的权重, 且满足:

投票法(voting)
投票法中最常用的是多数表决法。表决前需先将各自模型返回的预测置信度 si转化为预测类别,即最高置信度对应的类别标记 ci ∈ {1, 2, … , C} 作为该模型的预测结果。多数表决法中在得到样本 x 的最终预测时,若某预测类别获得一半以上模型投票,则该样本预测结果为该类别; 若对该样本无任何类别获得一半以上投票,则拒绝作出预测
投票法中另一种常用方法是相对多数表决法 , 与多数表决法会输出“拒绝预测”不同的是,相对多数表决法一定会返回某个类别作为预测结果, 因为相对多数表决是选取投票数最高的类别作为最后预测结果。
堆叠法
堆叠法又称“二次集成法”是一种高阶的集成学习算法。在刚才的例子中,样本 x 作为学习算法或网络模型的输入, si 作为第 i 个模型的类别置信度输出,整个学习过程可记作一阶学习过程。堆叠法则是以一阶学习过程的输出作为输入开展二阶学习过程, 有时也称作“元学习”。拿刚才的例子来说,对于样本 x , 堆叠法的输入是 N 个模型的预测置信
度 [s1,s2,...,sn] 这些置信度可以级联作为新的特征表示。之后基于这样的”特征表示”训练学习器将其映射到样本原本的标记空间。此时学习器可为任何学习算法习得的模型,如支持向量机,随机森林 ,当然也可以是神经网络模型。不过在此需要指出的是,堆叠法有较大过拟合风险。
参考文献
解析卷积神经网络——深度学习实践手册
版权声明:本文为CSDN博主「四月晴」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/siyue0211/article/details/80334924






