作者：CSDN 博主 Maples丶丶
在讲深度学习中优化算法之前，我想有必要对模型优化中常见的挑战有一个总览式的了解，这对于优化算法的理解还是有颇有裨益的。本篇博客是基于古德费洛的《Deep Learing》第8章和杨云的《深度学习实战》第五章总结归纳的。
学习和纯优化
机器学习中的优化过程也被称为是“学习”过程，它关注这样一类问题：寻找模型的一组参数 θ，它能显著地降低代价函数 J(θ)，该代价函数通常包括整个训练集上的性能评估和额外的正则化项。
需要注意的是，机器学习的优化算法通常是间接作用的。在大多数机器学习问题中，我们关注性能度量 P，其定义在测试集上并且可能是不可解的。我们希望通过降低代价函数 J(θ) 来提高 P，这样只是间接地优化 P 。而纯优化是最小化目标 J 本身。为了找到最优的 P，理想情况下我们希望最小化取自数据生成分布 pdata 的期望（至于为什么在《浅谈机器学习中的过拟合》有讲）：
其中LL是每个样本的损失函数，f( x ; θ ) 是输入 x 时的预测输出，y 是目标输出， pdata 是数据真实分布。
机器学习算法的目标是降低(1)式的期望泛化误差（也叫作风险），如果知道了真实分布 pdata( x , y )，那么最小化风险就变成了一个可以被优化算法解决的优化问题。但是在实际情况中，我们往往不可能知道 pdata( x , y )，只知道训练集中的样本。将机器学习转化回优化问题的最简单方法就是最小化训练集上的期望损失，即
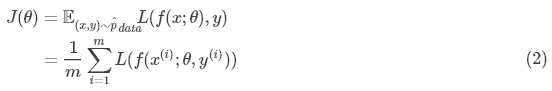
其中m是训练样本数目，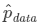
是经验分布，即训练集分布。最小化式(2)的训练过程被称为经验风险最小化。我们不直接最优化风险，而是最优化经验风险，同时希望能很大地降低风险。有点绕，大家仔细琢磨一下。
但是最优化经验风险很容易导致过拟合，高容量的模型会简单地记住训练集，很多情况下经验风险最小化并非真实可行。而且很多有用的损失函数，比如0-1损失，没有有效的梯度，无法使用基于梯度下降的算法进行优化。所以我们很少使用经验风险最小化，而是使用一个稍有不同的方法，比如用一个代理损失函数替代原目标函数，或者进行小批量训练。
有时候我们真正关心的损失函数不能被高效优化，通常我们会选择优化代理损失函数，即原目标的代理，某些情况下如果代理损失函数设计得当，还能比原函数学到更多。
优化中的挑战
传统机器学习会小心地设计目标函数和约束，确保优化问题是凸的，从而避免一般优化问题的复杂度。但在深度学习中因为模型的复杂性，我们必须经常面对非凸函数的优化问题，况且即使是凸优化，也并非没有任何问题。
病态
在凸函数优化中，Hessian矩阵HH的病态是最突出的一个问题。病态体现在随机梯度下降会“卡”在某些情况，这个时候即使很小的更新步长也会增加代价函数。
考虑函数 f(x) = A−1x，当 A ∈ Rn×n 具有特征值分解时，其条件数为
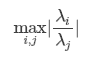
当条件数很大，即最大特征值和最小特征值差异很大时，函数对于输入的微小变化会变化得很剧烈。这种敏感性是矩阵本身的固有特性，当这种性质出现在网络参数更新过程中时，就非常致命了。回顾梯度下降的参数更新公式：
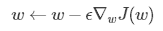
其中 ∇wJ(w) 通过二阶泰勒近似展开往往可以写成Hessian矩阵 H 和权重 w 乘积的形式，如果 H 是病态的，那么 w 很微小的改变都会使得 ∇wJ(w) 剧烈变化，使得训练过程极度不稳定。
局部极小值
对于凸函数而言，它的局部极小值就是它的全局最小值。而对于深度学习中我们经常要面对的非凸函数，局部极小值可能就没这么乐观了。但局部最优也没有那么可怕，对于机器学习而言，我们其实不太害怕局部最优解，害怕的是找到的解和全局最优相差很大，并且机器学习也并非只是一个纯粹的优化问题，在已知数据中找到最优解也不是机器学习的目的。在实践中我们发现，最优解附近的解其泛化性能通常也要比最优解好。
鞍点
鞍点也是临界点类型之一。当Hessian矩阵特征值全部为正时，只有局部极小值；全部为负时是局部极大值；当正负值都有时，是鞍点，即在某些维度上是极小值，在某些维度上是极大值。对于高维空间，鞍点的数量会远远大于局部极小值。试想一下，每个特征的正负由抛硬币决定，在一维情况下，很容易抛硬币得到正面朝上一次而获取局部极小点，而在 n 维空间中，要抛掷 n 次硬皮都正面朝上的难度是指数级的。
鞍点数量激增对于训练算法有哪些影响呢？对于只是用一阶梯度信息的优化算法而言，目前还没有权威的解释，一方面鞍点附近的梯度通常会非常小，另一方面实验中梯度下降似乎可以在许多情况下逃离鞍点。大佬Goodfellow也主张，连续时间的梯度下降会逃离而不是吸引到鞍点。对于牛顿法而言，目标是寻求梯度为0的点，如果没有适当的修改，牛顿法就会跳进一个鞍点再也出不来了。
梯度悬崖
多层神经网络通常存在像悬崖一样的斜率较大区域，这是由于几个较大的权重相乘导致的。当参数接近这样的悬崖区域时，梯度下降会很大程度地改变参数值，使参数弹射得非常远，可能会使大量已完成的优化工作成为无用功，如下图所示。
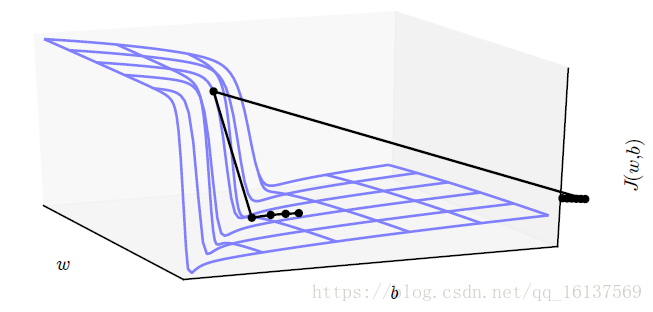
但幸运的是我们可以用梯度截断来避免其严重的后果。
梯度消失和梯度爆炸
深度学习最大的特点是其网络非常深，深度提升了模型的复杂度和能力，但也同时引发了梯度消失和梯度爆炸问题。梯度消失会使得我们难以确定参数优化方向，而梯度爆炸则会使得学习不稳定，梯度悬崖就是梯度爆炸的一种。
由于BP算法中链式求导法则的原因，第ll层权重的梯度大约要乘以 l∼n−1 层激活函数的导数和权重，如果我们使用sigmoid神经元，其导数最大值也才0.25，可想而知，乘的越多，最后得到的梯度就越小，最终发生了梯度消失。如果上层权重过大，经过传递后，本层的权重就会变得异常巨大，于是就发生了梯度爆炸。我们可以使用ReLU激活函数使每层激活函数的导数都为1来避免梯度消失，通过梯度截断来避免梯度爆炸。
非精确梯度
大多数优化算法的先决条件都是我们知道精确的梯度或Hessian矩阵。但在实践中几乎每一个深度学习算法都需要基于采样的估计，至少使用训练样本的小批量来计算梯度，因此我们实际使用的只是近似梯度。对于这个问题，我们可以选择比真实损失函数更容易估计的代理损失函数来避免这个问题。
版权声明：本文为CSDN博主「Maples丶丶」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_16137569/article/details/81633370
