常用的图像形态学操作包括膨胀、腐蚀、闭运算、开运算。
膨胀操作会扩大(粗化)图像中物体的轮廓,可以用来弥补(填充)物体间的孔洞,强化离散点,代价是导致物体的面积比原来的面积要大。
腐蚀操作会收缩(细化)图像中物体的轮廓,可以用来断开(分离)物体间的连接,消除离散点,代价是导致物体的面积比原来的面积要小。
闭运算是使用同一结构元对图像进行先膨胀后腐蚀的操作,可以用来弥合较窄的间断和细长的沟壑,消除物体间小的孔洞,填补轮廓线中的断裂。
开运算是使用同一结构元对图像进行先腐蚀后膨胀的操作,可以用来平滑物体的轮廓,断开物体间较窄的连接,消除物体边沿尖锐的突出部分。
需要说明的这些形态学操作所具有的效果是针对图像中物体属于高亮部分而言的,即前景物体的灰度高于背景图像。
这些形态学操作都涉及到一个关键的因子——结构元。结构元基本的形态是矩形、十字形或椭圆形(圆形)。
不管使用何种结构元形式,对被操作图像来说,总体效果总是一致的,那么问题是:
使用不同种结构元在效果上有哪些细微区别?
各结构元分别适用于那些场合?
一、各结构元在膨胀操作上差异
首先看一下需要被执行膨胀操作的原始图像:

对该灰度图像分别使用大小是7x7的矩形结构元、十字形结构元和椭圆形结构元,累计执行3次膨胀操作。
矩形结构元效果:

十字形结构元:

椭圆形结构元:

从三个不同结构元的膨胀效果分析:
1. 从膨胀和弥合的有效性看,矩形结构元为优。
可以从第三排中间的闪电形状的孔洞填补上对比出来,其他两个结构元还有孔洞,矩形结构元已经填补完成。
也就是说使用相同尺寸的结构元,相比其他两个结构元,矩形结构元能够执行最少次数的膨胀操作达到膨胀和弥合的目的。
2. 从膨胀之后的外形轮廓上分析:
矩形结构元倾向于使轮廓的拐点处具有水平或垂直分割的特征,上下左右四个方向的边界都是直的。
十字结构元倾向于使轮廓的拐点处具有四分之一十字结构元形状的锯齿。
椭圆结构元倾向于使轮廓的拐点处具有更为平滑和圆润的弧线。
可以简单概括为结构元的形状是什么,就使得膨胀之后的轮廓的拐点处像什么。
3. 从应用场合看,三者各有所长:
矩形结构元膨胀适用于对外形是规则形状、边沿处无太多尖锐突起的物体,这样可以最大程度保持物体原本的轮廓形状。
十字结构元膨胀适用于对外形不规则、边沿处有较多尖锐突起的物体,这样可以最大程度保持物体原本的轮廓形状。
椭圆结构元膨胀适用于要求对物体的轮廓进行平滑圆润处理的物体。
二、各结构元在腐蚀操作上差异
对原始灰度图像分别使用大小是5x5的矩形结构元、十字形结构元和椭圆形结构元,执行2次腐蚀操作。
矩形结构元效果:
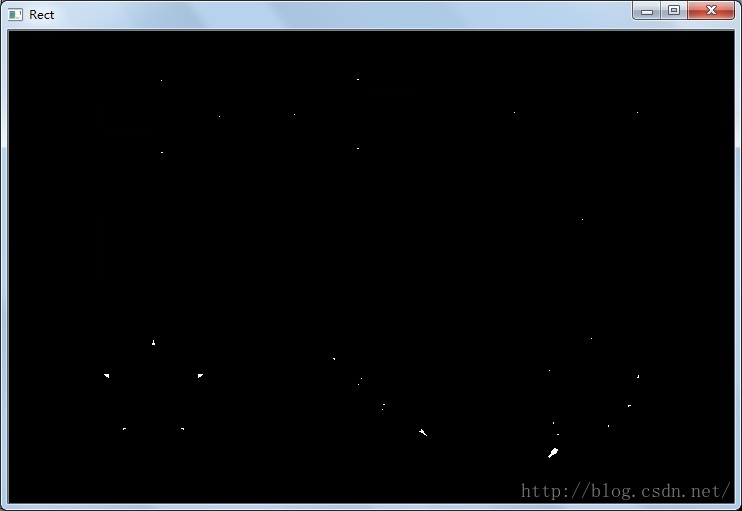
十字形结构元效果:

椭圆形结构元效果:
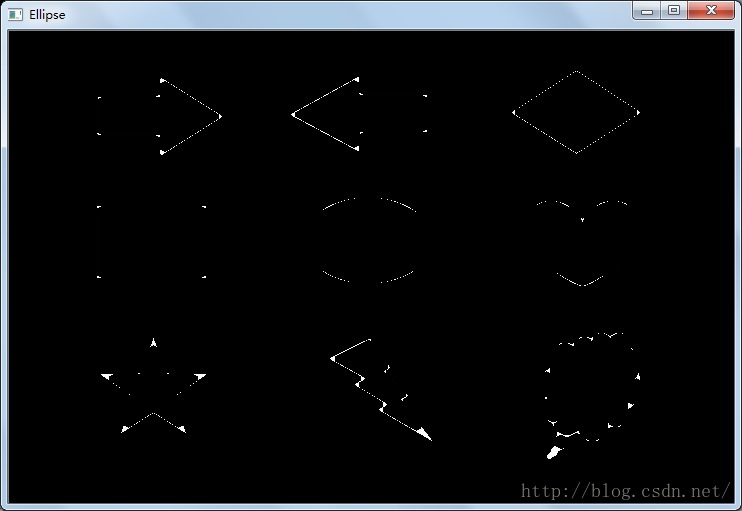
从三个不同结构元的腐蚀效果分析:
1. 从腐蚀的有效性看,矩形结构元为优。
进过同样尺寸同样此时腐蚀后,矩形结构元只剩下部分拐点处的散点没有腐蚀掉,其他两个结构元操作后物体的整 个轮廓仍较为清晰。
2. 从腐蚀之后的外形轮廓上分析:
矩形结构元腐蚀后只剩下部分拐点处的像素点,主要的是非直角的拐点。
十字结构元腐蚀的能力最弱,对所有拐点处都比较敏感。
椭圆结构元也是对所有拐点比较敏感。
3. 从应用场合看,除了矩形结构元所需腐蚀次数较少之外,好像并无其他明显区别。
来源:CSDN,作者:-牧野- ,转载此文目的在于传递更多信息,版权归原作者所有。
原文:https://blog.csdn.net/dcrmg/article/details/52265949
版权声明:本文为博主原创文章,转载请附上博文链接!






