上一篇 基于物理的渲染 – 理论篇(二)
菲涅尔方程
菲涅尔方程(Fresnel)定义的是在不同观察方向上,表面上被反射的光除以被折射的光的比例。在一束光击中了表面的一瞬间,菲涅尔根据表面与观察方向之间的夹角,计算得到光被反射的百分比。根据这个比例和能量守恒定律我们可以直接知道剩余的能量就是会被折射的能量。
当我们垂直观察每个表面或者材质时都有一个基础反射率,当我们以任意一个角度观察表面时所有的反射现象都会变得更明显(反射率高于基础反射率)。你可以从你身边的任意一件物体上观察到这个现象,当你以90度角观察你的桌子你会法线反射现象将会变得更加的明显,理论上以完美的90度观察任意材质的表面都应该会出现全反射现象(所有物体/材质都有菲涅尔现象)。
菲涅尔方程同样是个复杂的方程,但是幸运的是菲涅尔方程可以使用Fresnel-Schlick来近似:

F0表示的是表面基础反射率,这个我们可以使用一种叫做Indices of refraction(IOR)的方法计算得到。运用在球面上的效果就是你看到的那样,观察方向越是接近掠射角(与正视角相差90度),菲涅尔现象导致的反射就越强:

菲涅尔方程中有几个微妙的地方,一个是Fresnel-Schlick算法仅仅是为电介质表面定义的算法,对于金属表面,使用他们的折射率来计算基础反射率是不合适的,我们需要用别的菲涅尔方程来计算。对于这个问题,我们需要预先计算表面在正视角(即以0度角正视表面)下的反应(F0),然后就可以跟之前的Fresnel-Schlick算法一样,根据观察角度来进行插值。这样我们就可以用一个方程同时计算金属和电介质了。
表面在正视角下的反映或者说基础反射率可以在这个数据库中找到,下面是Naty Hoffman的课程笔记中列举的一些常见值:
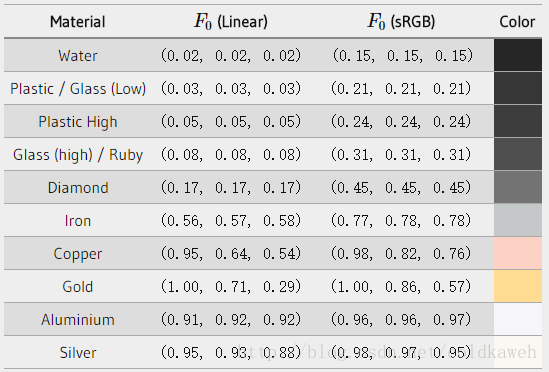
这里有个有趣的现象(不是定律),所有的电介质表面的基础反射率都没有超过0.17,而金属的基础反射率则高的多,大部分位于0.5到1.0之间。金属对不同颜色(波段)的光线的反射率是不一样的,这也是为什么反射率要分成RGB写的原因,这种现象我们只在金属表面发现过。
相比于电介质表面,金属表面的这些特殊属性引出了所谓的金属工作流,让我们通过一个名为金属度的额外参数来管理表面的材质,这个参数描述的是表面是金属还是非金属。
理论上来说表面金属度应该是一个布尔参数,要么是金属要么不是金属,是互斥的。然而,大多数渲染管线允许表面金属度参数的范围在0.0到1.0之间,这主要是因为材质纹理的精度不足以高到可以描述表面的灰尘之类的微小粒子,通过线性的金属度来表现这些细小的非金属颗粒,让我们可以得到更好的视觉效果。
使用预先计算好的导体和电介质的F0值,我们就能用同一个Fresnel-Schlick算法来模拟这两种类型的表面了,但是在金属表面上我们必须要对基础反射率着色,通常的做法类似下面的代码:
vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness);
我们定义一个电介质的基础反射率(0.04),这个值是通过电介质的常见基础反射率推测的一个经验参数,虽然不是准确的,但是能在降低了大量的材质管理复制度的同时实现很不错的效果。然后,根据表面的金属度来混合电介质的基础反射率和材质的本身基础反射率,因为金属会吸收所有折射光所以并没有漫反射颜色,我们可以直接使用表面的颜色来存储它的基础反射率.
(原文:https://learnopengl.com/#!PBR/Theory, 翻译:coldkaweh)
Fresnel Schlick近似算法写成代码:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}其中cosTheta是面法线n和观察方向v的点积。
Cook-Torrance反射方程
Cook-Torrance反射方程中的每一个部分我们我们都用基于物理的BRDF替换,可以得到最终的反射方程:

这个方程完整的定义了一个基于物理的渲染模型,这个方程是就是我们一般所说的基于物理的渲染。如果你还没有完全弄明白也别担心,我们将会把所有讨论的数学方法转化成代码。在下一个教程里,我们将要探索如何利用反射方程渲染出更好的光照效果,所有的知识碎片都会慢慢的融合到一起。
编辑PBR材质
对PBR数学模型有了基本了解之后,我们最后要讨论的是美工应该生成怎样的材质属性,让我们可以直接用在PBR渲染管线里。PBR管线中需要的所有材质参数都可以使用纹理来定义或者模拟,使用纹理我们可以逐像素控制制定的面如何跟光线交互:这个点是否是金属,粗糙度如何又或者表面对不同波长的光有什么反映。
下面你将会看到一些经常在PBR渲染管线中用作输入的纹理:

反射率(Albedo):反射率纹理指定了材质表面每个像素的颜色,如果材质是金属那纹理包含的就是基础反射率。这个跟我们之前用过的漫反射纹理非常的类似,但是不包含任何光照信息。漫反射纹理通常会有轻微的阴影和较暗的裂缝,这些在Albedo贴图里面都不应该出现,仅仅只包含材质的颜色(金属材质是基础反射率)。
法线(Normal):法线纹理跟我们之前使用的是完全一样的。法线贴图可以逐像素指定表面法线,让平坦的表面也能渲染出凹凸不平的视觉效果。
金属度(Metallic):金属度贴图逐像素的指定表面是金属还是电介质。根据PBR引擎各自的设定,金属程度即可以是[0.0,1.0]区间的浮点值也可以是非0即1的布尔值。
粗糙度(Roughness):粗糙度贴图逐像素的指定了表面有多粗糙,粗糙度的值影响了材质表面的微表面的平均朝向,粗糙的表面上反射效果更大更模糊,光滑的表面更亮更清晰。有些PBR引擎用光滑度贴图替代粗糙度贴图,因为他们觉得光滑度贴图更直观,将采样出来的光滑度使用(1-光滑度)= 粗糙度 就能转换成粗糙度了。
环境光遮挡(AO):AO贴图为材质表面和几何体周边可能的位置,提供了额外的阴影效果。比如有一面砖墙,在两块砖之间的缝隙里Albedo贴图包含的应该是没有阴影的颜色信息,而让AO贴图来指定这一块需要更暗一些,这个地方光线更难照射到。AO贴图在光照计算的最后一步使用可以显著的提高渲染效果,模型或者材质的AO贴图一般是在建模阶段手动生成的。
美工可以直接根据物体在真实世界里的物理属性,来设置和调整用于渲染的基于物理的材质。基于物理的渲染管线最大的优势在于,材质的物理属性是不变的,无论环境光怎么样设置都能得到一个接近真实的渲染结果,这让美工的人生都变得美好了。基于物理管线的材质可以很简单的移植到不同的渲染引擎,不管光照环境如何都能正确的渲染出一个自然的结果。
(原文:https://learnopengl.com/#!PBR/Theory, 翻译:coldkaweh)
进一步阅读
• Background: Physics and Math of Shading by Naty Hoffmann: there is too much theory to fully discuss in a single article so the theory here barely scratches the surface; if you want to know more about the physics of light and how it relates to the theory of PBR this is the resource you want to read.
• Real shading in Unreal Engine 4: discusses the PBR model adopted by Epic Games in their 4th Unreal Engine installment. The PBR system we’ll focus on in these tutorials is based on this model of PBR.
• Marmoset: PBR Theory: an introduction to PBR mostly meant for artists, but nevertheless a good read.
• Coding Labs: Physically based rendering: an introduction to the render equation and how it relates to PBR.
• Coding Labs: Physically Based Rendering - Cook–Torrance: an introduction to the Cook-Torrance BRDF.
• Wolfire Games - Physically based rendering: an introduction to PBR by Lukas Orsvärn.
原文链接:https://learnopengl.com/#!PBR/Theory
本文转自:CSDN,译者:coldkaweh,转载此文目的在于传递更多信息,版权归原作者所有。
原文链接:https://blog.csdn.net/coldkaweh/article/details/70187399






