数字图像处理技术的研究与开发对数学基础的要求很高,一些不断涌现的新方法中,眼花缭乱的数学推导令很多期待深入研究的人望而却步。图像处理研究中所需的数学原理基础,主要涉及微积分、向量分析、场论、泛函分析、偏微分方程、复变函数、变分法等。
虽然一个理工科学生大致已经具备了包括微积分、线性代数、概率论在内的数学基础,但在分析一些图像处理算法的原理时,好像还是感觉无从入手。
在研究图像处理最容易碰到的一些知识点,需要采取一种循序渐进的方式将它们重新组织到了一起。并结合具体的图像处理算法讨论来讲解这些数学知识的运用,从而建立数学知识与图像处理之间的一座桥梁。
下面是一些常用的数学方法:
1. 积分类型的数学变换
基本思想是利用各种积分变换将信号从时域或空域投影到变换域。目的是利用人为设定的基函数对原始信号进行投影,使变换系数表现出某种良好的性质,实质就是对信号的另一种等价表达方式。

积分变换就是通过参变量积分将一个已知函数变为另一个函数。变换性能取决于基函数的选择,经典的就是傅里叶变换和小波变换。数学变换会追求所谓稀疏表示,即如何通过最小数量的系数尽可能更多的描述信号的能量。不同类型的信号,其在不同变换下系数的分布会不同。
2. 基于偏微分的曲线
基本思想是利用极小化能量泛函的解实现曲线曲面的变化,对常微分方程进行求解,但是我们不能忽视由于某些原因有许多定解问题是不能严格解出的,只可以用近似方法求出满足实际需要的近似程度的近似解,最终使其逼近我们所期望的结果。
3. 统计分析
这是现代信号处理和统计模式识别的基础,现代信号处理追求的是某种统计意义下的最优滤波,所以我们会看到MMSE、MLS之类的滤波算法。统计模式识别重点放在分类界面的确定,这需要以先验概率作为前提;若先验概率未知,则通过有参或无参方法对其进行估计。
统计方法主要通过利用概率论建立数学模型,收集所观察系统的数据,进行量化的分析、总结,并进而进行推断和预测,为相关决策提供依据和参考。它被广泛的应用在各门学科之上,从物理和社会科学到人文科学,甚至被用来工商业及政府的情报决策之上。
4. 非线性离散滤波器
滤波器是信号处理中最重要的研究对象,滤波器可以将原始信号的有用信息通过各种组合来凸显出来,基本上所有涉及到特征的应用场合都要考虑滤波器,如果滤波器设计得好的话,能够极大地提高整个算法的准确度和效率。典型的滤波器有序统计滤波、中值滤波、中值滤波。Lee滤波等等。
在实际应用中,非线性滤波算法的选取还应根据具体应用场合和条件,并需要在估计精度、实现难易程度、数值稳健性及计算量等各种指标之间综合权衡。比如,在雷达对再入飞行目标进行跟踪问题中,由于目标速度极快,受到复杂的空气动力影响而呈现出很强的非线性,通常用UKF方法更适合。
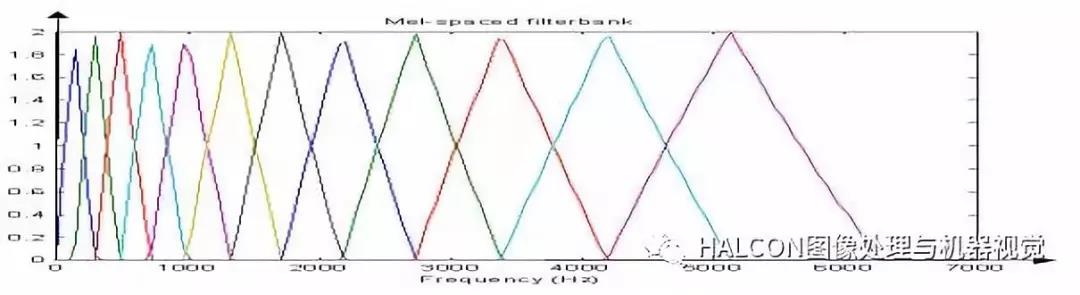
5. 多分辨率分析
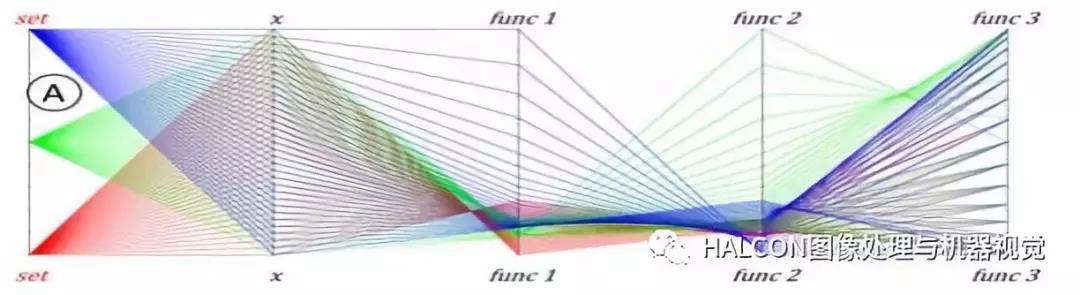
是小波变换在实际工程应用中的一个重要方向,其实小波只是其中一种,基本思想与多抽样率滤波器组相一致,建立了小波变换与数字滤波器之间的联系。多分辨率分析是一个框架,可以选择不同的滤波器。为正交小波基的构造提供了简单的分析方法,而且为正交小波变换的快速算法提供了理论依据。

小波变换由于能同时在时域和频域中对信号进行分析,能有效地区分信号中的突变部分和噪声,从而实现信号的消噪在信号处理领域,用小波分析降噪已得到越来越广泛的应用。比如小波阈值去噪法是小波去噪方法中应用较广泛的一种,它具有方法简单、计算量小和去噪效果好的特点。
本文转自:微信号 - HALCON图像处理与机器视觉(NeXt8060),转载此文目的在于传递更多信息,版权归原作者所有。






