正则项的理解之正则从哪里来

本文来自合肥工业大学电子商务研究所刘业政老师的上课总结。感谢刘老师。哈哈。

人类认识世界的过程可以理解成是对世界上的事物进行分类的过程。没有分类的能力，人类的认知将无法进行。因此，我们从分类的角度来说明这个问题。

一、线性可分与线性不可分

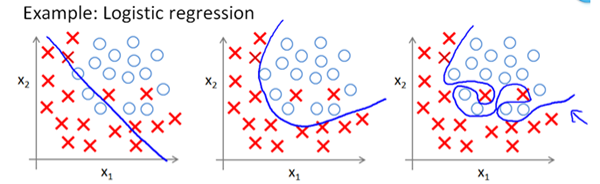
说到分类就要说到线性可分和线性不可分。这是属于模式识别中的概念。在欧几里德几何中，线性可分是一组点的集合性质。最容易描述的情况是在二维平面中，有一些点，分别是红色的点和蓝色的点。如果我们可以使用一条直线将不同颜色的点分开，那么这些点就是线性可分的。确定一组点是否线性可分就是看是否能找到一个超平面将这些点分开。超平面就是n维欧式空间中余维度等于一的线性子空间，也就是必须是(n-1)维度。例如平面中的线、空间中的平面等就是二维空间和三维空间的超平面。如下图所示，是二维空间线性可分与线性不可分的例子。

图 1

有了线性可分的概念之后，我们就可以构造分类器来帮助我们对目标对象进行分类。比如，数据是p维的向量，那么我们就可以构造一个(p-1)维的超平面来将数据分开。如图1所示中第一个线性可分的情况，假设我们要将一个二维平面的点分开。那么我们可以构造一个分类器，即一个线性函数：

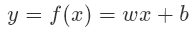
我们希望这个方程可以将不同颜色的点分开，也就是说需要求的一组参数w和b，得到一个函数。使得所有的红色的点都在线的左边，蓝色的点在线的右边。

图 2

总结一下，在机器学习的分类任务中。我们需要构造一个分类模型 Y = F(X)，使得它能很好的判别数据所属的类别。假设我们有N个训练数据 { x_i , y_i }，那么该分类器的目标（函数）是：

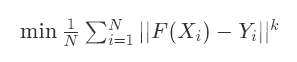
这里的N是样本规模，k是范数的阶，可取 k = 0 , 1 , 2 ,…

以上是机器学习中分类模型的简单总结。不懂的同学自己可以去补补课，这不是本文的重点，过程不细说了，我们只用这个形式。

二、过拟合和欠拟合

但是，在实际情况中，并不是所有的数据都是线性可分的。如图2中对平面中的点进行分类就不是线性可分的。其中点是二维空间的点，第一个图使用的分类器是线性分类器即 wx + b ，但是这时候分类并不好。第二个图的分类器是增加一个维度后的，是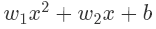，这时候分类比较不错。如果是第三个图的分类器（图形不是，我们假设是三次方的），则变成了，那么这时候就过拟合了。可以看到增加空间维数会显著增加参数，使得计算复杂度增高，也可能引起过拟合的问题。

从这个例子中我们可以看到，在线性不可分的情况下，如果我们还在当前维度构造分类器就会产生欠拟合的情况，如图2中最左边的图所示。这时候我们可以将空间映射到高维空间中，这时候就数据在高维中就线性可分了。如图3所示，在二维平面上线性不可分的点映射到三维空间后可以使用一个平面做到线性可分了。但是如果我们增加的空间的维数过高，那么会增加大量的参数从而导致过拟合，如上图3中最右边的图所示。欠拟合的一是是指分类器不能很好的对当前的数据进行分类，而过拟合的意思是分类器对训练数据过分拟合，导致对训练集的分类效果很好，但是由于噪音等的存在，这个很好的分类能力在面对新的数据的时候分类能力反而下降了。

图 3

三、期望风险、经验风险和结构风险

我们从另一个角度来理解一下前面说的欠拟合和过拟合的问题。在机器学习中，我们一般会遇到三种风险，即期望风险、经验风险和结构风险。这里我们简要介绍一下，因为过拟合其实就是只考虑经验风险，忽视结构风险导致的结果。

3.1、期望风险

首先，我们说一下我们机器学习的目标是希望模型的预测结果与数据真实的输出结果一致。这显然不可能。所以我们定义一个函数来度量模型的预测值与真实值之间的差距，也就是模型的拟合能力。可以通过定义代价函数（或者叫损失函数）来描述模型与数据之间的差距：

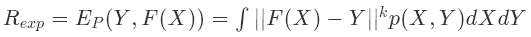
注意到，代价函数描述的是数据总体与模型之间的差别。代价函数定义的就是我们常说的期望风险，即模型对总体数据的拟合能力。我们的目标是期望风险越小越好，期望风险越小，模型拟合能力越强。显然，在实际中期望风险函数是很难获取的，因为我们难以知道数据总体分布是什么。因此，我们需要定义其他风险函数来代替期望风险。

3.2、经验风险

前面我们提到了机器学习分类任务的目标函数，在训练模型的过程中，分类的目标简单来说就是希望样本真实值与预测值之间的差别尽可能小。而我们对某个样本的预测值结果与其真实值之间的差距就是损失，可以使用上述差值来定，因此也称之为损失函数。损失函数的值其实是一个随机变量，因为它依赖于一个随机变量的输出（即依赖于输入值）。因此，我们一般通过损失函数的期望来做决策。我们已经说过，损失函数是指样本预测值与真实值之间的差值。这个差值的定义可以是零阶的、一阶的、二阶的等，甚至是对数的。

通过损失函数我们可以知道模型对单个样本的预测能力。如果想知道模型对所有样本的预测能力，只要将该损失函数在所有样本下累加即可。因此，最好的分类模型应当是损失函数结果全为0，即预测值与真实值之间完全一样。这在现实中显然不可能，但是我们可以把损失函数当做我们的目标函数，损失函数的值越小，证明我们预测的越准确。损失函数定义的就是我们常说的经验风险，即：

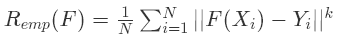
这里的 x_i 是输入值，Y_i​​ 是输入对应的真实值，F( x_i​​ )是我们的预测值。N 是样本的个数。

经过上面的讨论，我们知道这里的损失函数定义的是针对样本数据即训练集的风险函数，称之为经验风险，它针对的是训练数据，也就是我们的模型对训练数据的拟合能力。经验风险越小，模型对训练集的拟合能力越好。显然，使用经验风险代替期望风险也是有问题的，因为这个风险函数无法度量模型对新数据的预测能力。

3.3、置信风险与结构风险

尽管如此，我们还是希望模型的经验风险越小越好，因为它证明了模型对训练数据的拟合能力。当然，将经验风险作为唯一的目标函数来优化模型是不够的。因为，训练数据中可能有噪音，它也不能代表总体，因此，对训练数据拟合的很好不一定意味着模型对测试数据拟合能力也好。只考虑经验风险的模型会出现我们前面说的过拟合现象。也就是说，我们可以定义一个高维的模型，它可以很好的对原来的数据进行分类建模。然而，高维的模型函数太复杂，参数太多，所以很容易出现过拟合的现象。因此，我们需要定一个新的风险函数，使得模型在优化经验风险的同时，可以降低本身的复杂度。这就是结构风险函数。其定义如下：

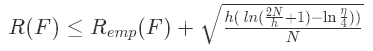
也就是说结构风险等价于经验风险+置信风险，上式右边的第二项就是机器学习中分类函数的VC维的置信区间。VC维的置信区间描述的是模型在未知文本上预测的误差。详细的关于置信风险的来历以及VC维的知识我们在后面给出新的介绍，这里简单说一下。VC维是描述在样本集上有效的假设数量的个数。意思就是针对一个数据，我们的假设空间（可以简单理解为模型的数量）很大，但是这对我们寻找一个最好的假设空间来近似理想的方案（真实的模型）是不利的，所以我们需要寻找一个理论的数据，使得假设空间不大于这个数值，这样对我们求理想解有理论上的帮助。VC维的概念就是帮助我们理解假设空间数量的。这里我们用到VC最终的结论，即VC维的大小：与学习算法无关，与输入变量的分布也无关，与我们求解的目标函数无关。它只与模型和假设空间有关。VC维反映了假设空间H的强大程度(powerfulness)，VC维越大，H也越强，因为它可以打散(shatter)更多的点。

也就是说，VC维越大，模型推广能力越差（因为假设空间越广泛），置信风险也就越大。在模型上就是模型变得很复杂。所以结构风险的目标是在保证经验风险小的时候，要求置信风险也很小。

四、正则的作用

前面说了这么多，我们总结一下，在机器学习中，模型的目标是拟合数据。但是我们也不希望模型出现过拟合的现象。也就是说，我们对模型的要求是经验风险和结构风险同时很小。也就是说在模型拟合能力好的同时，要降低模型的复杂度，来获得模型更好的泛化能力。而降低模型的复杂度有两条路径：一是进行降维，进行特征约减，这样可以减少模型参数的个数。二是对参数进行约束。使得参数的取值范围减少。而第二种方法就是加正则项。

增加了正则项之后，新的模型的假设空间会受到限制，此时模型的VC维会变小，也就是模型的泛化能力更强。我们的新目标函数是：

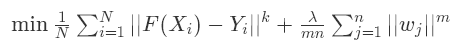
这里的 n 是指模型中参数的数量，λ 是正则项系数，m 是正则项的阶，可以取0，1，2，……

以0-阶正则为例，也就是说，模型的参数要么是0，要么是1，这显然大大降低了模型参数的个数。但是0-阶范数的求解是一个NP难问题，显然这不符合我们的要求。那么1-阶范数呢？1-阶范数同样可以降低模型的复杂度，但是一阶范数的求导又比较困难。所以一般情况下，正则项我们可以取二阶范数。

五、正则项的其他理解

出了上述机器学习中对正则项的理解，我们还有两种方式去理解正则项的含义。

5.1、拉格朗日乘数

在数学中的最优化问题中，拉格朗日乘数法（以数学家约瑟夫·拉格朗日命名）是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组新的未知数，即拉格朗日乘数，又称拉格朗日乘子，或拉氏乘子，它们是在转换后的方程，即约束方程中作为梯度（gradient）的线性组合中各个向量的系数。

微积分中最常见的问题之一是求一个函数的极大极小值（极值）。但是很多时候找到极值函数的显式表达是很困难的，特别是当函数有先决条件或约束时。拉格朗日乘数则提供了一个非常便利方法来解决这类问题，而避开显式地引入约束和求解外部变量。

在机器学习中，我们的目标函数是：

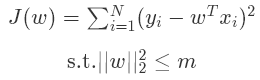
这个形式正好是带约束的求极值问题。利用拉格朗日乘法可以将该带约束的求极值问题转换成新函数的求极值问题：

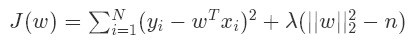
看到了这两个公式等价，也就是说正则化的本质就是给未知参数带来一定的约束。

5.2、贝叶斯先验

正则项的另一个理解是通过概率矩阵分解中的先验。参考推荐系统之概率矩阵分解的详细推导过程。在没有先验的矩阵分解的推导中，我们得到的公式是：

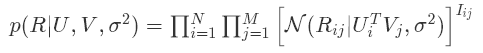
当U和V分别有了先验参数之后：

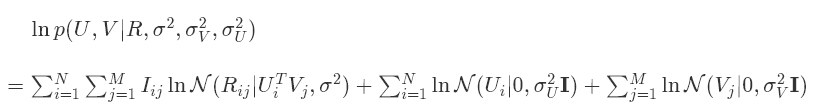
注意，这里我们加了一个对数函数。可以看到，加了先验之后的概率矩阵分解的结果多了未知参数的先验，如果先验是高斯分布，那么转化后和前面的二阶范数正好类似。

总结

最后总结一下，正则项是通过增加模型参数的约束来降低模型的过拟合情况。背后的原理是模型既要降低经验风险也要降低结构风险，而降低结构风险背后的原来来源于VC维的概念。

参考文献1：《机器学习中的数学基础》.刘业政.合肥工业大学.管理学院.电子商务研究所
参考文献2：http://blog.csdn.net/liyajuan521/article/details/44565269
参考文献3：https://www.zhihu.com/question/52398145
参考文献4：https://www.zhihu.com/question/38607822
参考文献5：http://www.flickering.cn/machine_learning/2015/04/vc%E7%BB%B4%E7%9A%84%E...
参考文献6：https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9...
参考文献7：http://blog.csdn.net/wsj998689aa/article/details/39547771

本文转自：数据学习者官方网站，转载此文目的在于传递更多信息，版权归原作者所有。