对于数字图像处理而言,一般包含着空间域处理和变换域处理两种形式。空间域处理方法主要是直接以图像中的像素操作为基础,它主要分为灰度变换和空间滤波两类。灰度变换是在图像的单个像素上操作,主要以对比度和阈值处理为目的。
空间域处理可由下式表示:
g ( x , y ) = T [ f ( x , y ) ]
其中 f ( x , y ) 是输入图像,g ( x , y ) 是处理后的图像,T 是在点 ( x , y ) 的领域上定义的关于 f 的一种算子。
为了保证经过灰度变换后的输出图像在整体的外貌上,或者更准确地说在形态学上,与输入图像保持一致,灰度变换函数必须是严格单调递增函数。在图像处理中,灰度变换主要应用于图像的对比度改善。在灰度变换中,最为常用的三类基本函数为线性函数(反转和恒等变换)、对数函数(对数和反对数变换)以及幂律函数(n次幂和n次根变换)。恒等函数是最一般的情况,其输出图像灰度等于输入图像灰度的变换。
1、图像反转
图像反转的表达式:s = L - 1 - r 。其中r表示处理前的灰度值,s表示处理后的灰度值。采取这种方式反转一副图像的灰度级,可得到等效的照片底片。特别适用于增强嵌入在一副图像的暗区域中的白色或者灰色细节,尤其是当黑色面积在尺寸上占主导地位时。
2、对数变换
对数变换的通用形式为:
s = c log( 1 + r )
其中 c 是一个常数,并假设 r ≥ 0,其变换曲线如下图
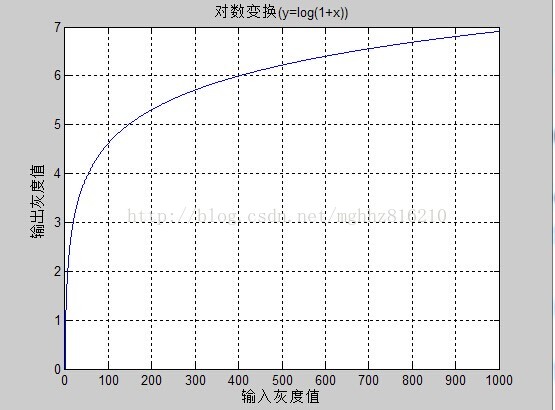
对数变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值,相反,对高的输入灰度值也是如此。也就是说,该变换扩展图像的低灰度范围,同时压缩图像的高灰度范围。
3、幂律变换
幂律变换的基本表达式为:
s = crγ
其中c和γ为正常数。其一般表达式的图像为:
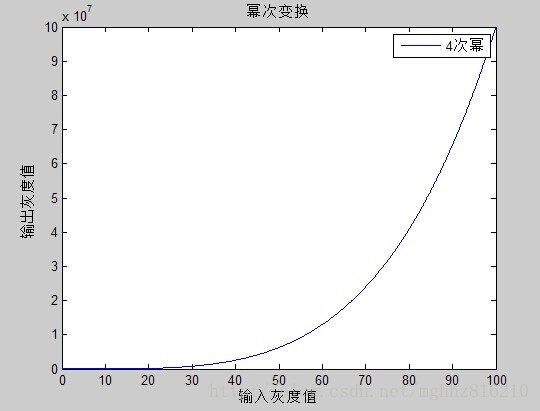
对于 γ < 1,扩展低灰度范围,压缩高灰度范围;对于 γ > 1,压缩低灰度范围,扩展高灰度范围。
4、分段线性变换函数
对比度拉伸是最简单的分段线性函数。其一般的函数图像为:
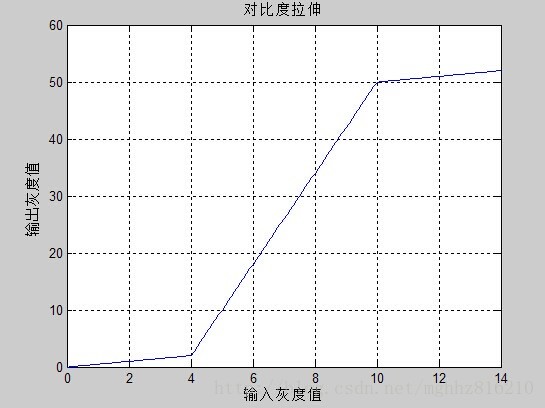
本文转自:CSDN - 學绘o嗿翫,转载此文目的在于传递更多信息,版权归原作者所有。
原文:https://blog.csdn.net/xuehuitanwan123/article/details/81605712






