一、超参数选择
Grid Search
- 网格搜索
- 在高维空间中对一定区域进行遍历
Random Search
- 在高维空间中随机选择若干超参数
二、余弦相似度(Cos距离)与欧氏距离的区别和联系
- 欧式距离和余弦相似度都能度量 2 个向量之间的相似度
- 放到向量空间中看,欧式距离衡量两点之间的直线距离,而余弦相似度计算的是两个向量之间的夹角
- 没有归一化时,欧式距离的范围是 (0, +∞],而余弦相似度的范围是 (0, 1];余弦距离是计算相似程度,而欧氏距离计算的是相同程度(对应值的相同程度)
- 归一化的情况下,可以将空间想象成一个超球面(三维),欧氏距离就是球面上两点的直线距离,而向量余弦值等价于两点的球面距离,本质是一样。
三、欧式距离vs曼哈顿距离
欧式距离L2 :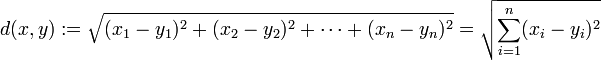
欧氏距离虽然很有用,但也有明显的缺点。它将样品的不同属性(即各指标或各变量量纲)之间的差别等同看待,这一点有时不能满足实际要求。例如,在教育研究中,经常遇到对人的分析和判别,个体的不同属性对于区分个体有着不同的重要性。因此,欧氏距离适用于向量各分量的度量标准统一的情况
曼哈顿距离L1 :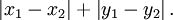
曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。当坐标轴变动时,点间的距离就会不同
本文转自:CSDN - LinLin_coder,转载此文目的在于传递更多信息,版权归原作者所有。
原文链接:https://blog.csdn.net/weixin_41108334/article/details/86499552






