6个常用的聚类评价指标

评估聚类结果的有效性，即聚类评估或验证，对于聚类应用程序的成功至关重要。它可以确保聚类算法在数据中识别出有意义的聚类，还可以用来确定哪种聚类算法最适合特定的数据集和任务，并调优这些算法的超参数(例如k-means中的聚类数量，或DBSCAN中的密度参数)。

虽然监督学习技术有明确的性能指标，如准确性、精度和召回率，但评估聚类算法更具挑战性：

由于聚类是一种无监督学习方法，因此没有可以比较聚类结果的基础真值标签。

确定“正确”簇数量或“最佳”簇通常是一个主观的决定，即使对领域专家也是如此。一个人认为是有意义的簇，另一个人可能会认为是巧合。

在许多真实世界的数据集中，簇之间的界限并不明确。一些数据点可能位于两个簇的边界，可以合理地分配给两个簇。

不同的应用程序可能优先考虑簇的不同方面。例如，在一个应用程序中，可能必须有紧密、分离良好的簇，而在另一个应用程序中，捕获整体数据结构可能更重要。

考虑到这些挑战，通常建议结合使用评估指标、视觉检查和领域专业知识来评估簇性能。

一般来说，我们使用两种类型的聚类评估度量(或度量):

内部：不需要任何基础事实来评估簇的质量。它们完全基于数据和聚类结果。

外部：将聚类结果与真值标签进行比较。（因为真值标签在数据中是没有的，所以需要从外部引入）

通常，在实际的应用程序中，外部信息(如真值标签)是不可用的，这使得内部度量成为簇验证的唯一可行选择。

在本文中，我们将探讨聚类算法的各种评估指标，何时使用它们，以及如何使用Scikit-Learn计算它们。

内部指标

由于聚类的目标是使同一簇中的对象相似，而不同簇中的对象不同，因此大多数内部验证都基于以下两个标准:

紧凑性度量：同一簇中对象的紧密程度。紧凑性可以用不同的方法来衡量，比如使用每个簇内点的方差，或者计算它们之间的平均成对距离。

分离度量：一个簇与其他簇的区别或分离程度。分离度量的例子包括簇中心之间的成对距离或不同簇中对象之间的成对最小距离。

我们将描述三种最常用的内部度量方法，并讨论它们的优缺点。

1、轮廓系数

轮廓系数(或分数)通过比较每个对象与自己的聚类的相似性与与其他聚类中的对象的相似性来衡量聚类之间的分离程度[1]。

我们首先定义数据点x的轮廓系数为：

这里的A (x′)是x′到簇中所有其他数据点的平均距离。或者说 如果点x∈属于簇C∈，那么

其中d(x, xⱼ)是点x和x之间的距离ⱼ。我们可以将a(x ^ e)解释为点x ^ e与其自身簇匹配程度的度量(值越小，匹配越好)。对于大小为1的簇，a(x′f)没有明确定义，在这种情况下，我们设s(x′f) = 0。

B (x′)是x′与相邻簇中点之间的平均距离，即点到x′的平均距离最小的簇：

轮廓系数的取值范围为-1到+1，值越高表示该点与自己的聚类匹配得越好，与邻近的聚类匹配得越差。

基于样本的轮廓系数，我们现在将轮廓指数(SI)定义为所有数据点上系数的平均值：

这里的n为数据点总数。

轮廓系数提供了对聚类质量的整体衡量:

接近1意味着紧凑且分离良好。

在0附近表示重叠。

接近-1表示簇的簇太多或太少。

sklearn的Metrics提供了许多聚类评估指标，为了演示这些指标的使用，我们将创建一个合成数据集，并使用不同的k值对其应用k-means聚类。然后，我们将使用评估指标来比较这些聚类的结果。

首先使用make_blobs()函数从3个正态分布的聚类中随机选择500个点生成一个数据集，然后对其进行归一化，以确保特征具有相同的尺度：

 from sklearn.datasets import make_blobs
 from sklearn.preprocessing import StandardScaler
 
 X, y = make_blobs(n_samples=500, centers=3, cluster_std=0.6, random_state=0)
 X = StandardScaler().fit_transform(X)

让我们来绘制数据集：

def plot_data(X):
    sns.scatterplot(x=X[:, 0], y=X[:, 1], edgecolor='k', legend=False)
    plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
 
 plot_data(X)

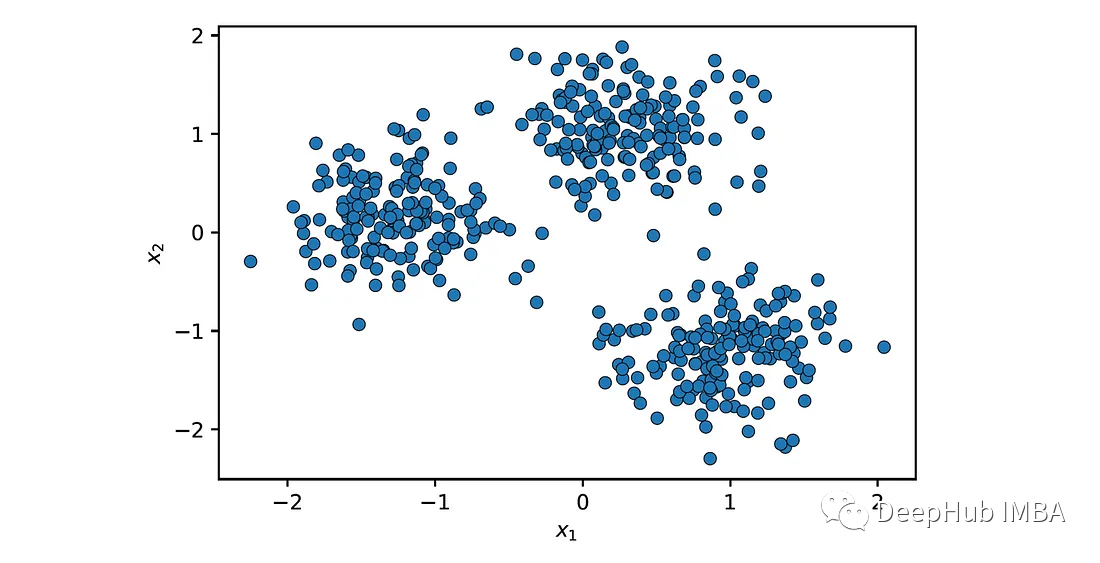
然后在k = 2,3,4运行k-means聚类，并将聚类结果存储在三个不同的变量中:

 from sklearn.cluster import KMeans
 
 labels_k2 = KMeans(n_clusters=2, random_state=0).fit_predict(X)
 labels_k3 = KMeans(n_clusters=3, random_state=0).fit_predict(X)
 labels_k4 = KMeans(n_clusters=4, random_state=0).fit_predict(X)

现可以使用函数sklearn.metrics.silhouette_score()来计算每轮廓分数。

from sklearn.metrics import silhouette_score
 
 print(f'SI(2 clusters): {silhouette_score(X, labels_k2):.3f}')
 print(f'SI(3 clusters): {silhouette_score(X, labels_k3):.3f}')
 print(f'SI(4 clusters): {silhouette_score(X, labels_k4):.3f}')

结果如下：

 SI(2 clusters): 0.569
 SI(3 clusters): 0.659
 SI(4 clusters): 0.539

可以看到当k = 3时，得分最高，并且低于1，这表明簇之间没有完全分离。

为了计算每个样本的轮廓系数，我们可以使用函数sklearn.metrics.silhouette_samples。基于这些系数，可以建立一个轮廓图，它提供了一种评估每个对象在其簇中的位置的方法。在这张图中，每个点的轮廓系数用一条水平线表示(更长的条形表示更好的聚类)。这些条按簇排列和分组。每个聚类部分的高度表示该聚类中的点的数量。

 import matplotlib.cm as cm
 from sklearn.metrics import silhouette_samples
 
 def silhouette_plot(X, cluster_labels):
    n_clusters = len(np.unique(cluster_labels))
    silhouette_avg = silhouette_score(X, cluster_labels)
 
    # Compute the silhouette coefficient for each sample
    sample_silhouette_values = silhouette_samples(X, cluster_labels)
 
    y_lower = 10
    for i in range(n_clusters):
        # Get the silhouette coefficients for samples in cluster i and sort them
        cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
        cluster_silhouette_values.sort()
 
        # Compute the height of the cluster section
        cluster_size = len(cluster_silhouette_values)
        y_upper = y_lower + cluster_size
 
        # Plot the coefficients for cluster i using horizontal bars
        color = cm.nipy_spectral(float(i) / n_clusters)
        plt.fill_betweenx(np.arange(y_lower, y_upper), 0, cluster_silhouette_values,
                          facecolor=color, edgecolor=color, alpha=0.7)
 
        # Show the cluster numbers at the middle
        plt.text(-0.05, y_lower + 0.5 * cluster_size, str(i))
 
        # Compute the new y_lower for the next cluster
        y_lower = y_upper + 10
 
    # Draw a vertical line for the average silhouette score
    plt.axvline(x=silhouette_avg, color='red', linestyle='--')
 
    plt.yticks([]) # Clear the yaxis labels / ticks    
    plt.xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
     
    plt.xlabel('Silhouette coefficient values')
    plt.ylabel('Cluster label')

k = 3的k-means聚类轮廓图为：

k = 4：

在第二张图中，我们可以看到类0和类3中的大多数点的轮廓分数低于平均分数。这表明这些聚类可能不代表数据集中的自然分组。

让我们总结一下轮廓分数的利弊。

优点：

• 很容易解读。它的取值范围是-1到1，接近1的值表示分离良好的簇，接近-1的值表示聚类较差。

它不仅提供了对整体簇质量的洞察，还提供了对单个簇质量的洞察。这通常使用一个轮廓图来可视化，它显示了簇中的每个点对总体得分的贡献。

它可以通过比较不同k值的分数并取最大值来确定k-means等算法中的最优簇数。这种方法往往比肘部法更精确，因为肘部法往往需要主观判断。

缺点：

倾向于支持凸簇，而非凸或不规则形状的簇可能表现不佳。

不考虑簇的密度，这对于评估基于密度的算法(如DBSCAN)很重要。

当簇之间存在重叠时，轮廓评分可能提供模糊的结果。

可能难以识别较大簇中的子簇。

计算量很大，因为它需要计算所有O(n²)个点之间的成对距离。这可能会使评估过程比聚类本身更昂贵(例如，当使用k-means时)。

对噪声和异常值敏感，因为它依赖于可能受异常值影响的最小成对距离。

2、方差比准则（Calinski-Harabasz Index）

由于Calinski-Harabasz指数的本质是簇间距离与簇内距离的比值，且整体计算过程与方差计算方式类似，所以又将其称之为方差比准则。

K是簇的数量，N是数据点的总数BCSS (between - cluster Sum of Squares)是每个聚类质心(mean)与整体数据质心(mean)之间欧氏距离的加权平方和：

其中n′′是簇i中数据点的个数，c′′是簇i的质心(均值)，c是所有数据点的总体质心(均值)。BCSS衡量簇之间的分离程度(越高越好)。

WCSS (Within-Cluster Sum of Squares)是数据点与其各自的聚类质心之间的欧氏距离的平方和：

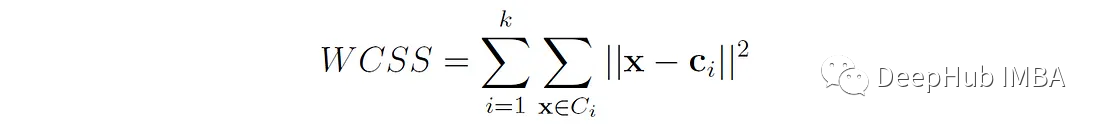
WCSS度量簇的紧凑性或内聚性(越小越好)。最小化WCSS(也称为惯性)是基于质心的聚类(如k-means)的目标。

CHI的分子表示由其自由度k - 1归一化的簇间分离(固定k - 1个簇的质心也决定了第k个质心，因为它的值使所有质心的加权和与整个数据质心匹配)。CHI的分母表示由其自由度n- k归一化的簇内离散度(固定每个簇的质心会使每个簇的自由度减少1)。

将BCSS和WCSS按其自由度划分有助于使值规范化，使它们在不同数量的簇之间具有可比性。如果没有这种归一化，CH指数可能会因k值较高而被人为夸大，从而很难确定指标值的增加是由于真正更好的聚类还是仅仅由于簇数量的增加。

CHI值越高，表示聚类效果越好，因为这意味着数据点在聚类之间的分布比在聚类内部的分布更分散。

在Scikit-Learn中，我们可以使用函数sklearn.metrics.calinski_harabasz_score()来计算这个值。

 from sklearn.metrics import calinski_harabasz_score
 
 print(f'CH(2 clusters): {calinski_harabasz_score(X, labels_k2):.3f}')
 print(f'CH(3 clusters): {calinski_harabasz_score(X, labels_k3):.3f}')
 print(f'CH(4 clusters): {calinski_harabasz_score(X, labels_k4):.3f}')

结果如下：

 CH(2 clusters): 734.120
 CH(3 clusters): 1545.857
 CH(4 clusters): 1212.066

当k = 3时，CHI得分最高，这也跟上面的轮廓系数得到的结果一样。

Calinski-Harabasz指数的优缺点如下：

优点：

• 计算简单，计算效率高。

• 很容易理解。数值越高通常表示聚类效果越好。

• 像轮廓系数一样，它可以用来找到最优的簇数。

• 有一定的理论依据(它类似于单变量分析中的f检验统计量，它比较组间方差和组内方差)。

缺点：

• 倾向于支持凸簇，对于不规则形状的簇可能表现不佳。

• 可能在不同大小的簇中表现不佳，因为大型簇内的方差会不成比例地影响BCSS和WCSS之间的平衡。

• 不适合评估像DBSCAN这样基于密度的簇。

• 对噪声和异常值敏感，因为这些会显著影响簇内和簇间的分散。

3、Davies-Bouldin指数(DB值)

戴维斯-博尔丁指数(Davies-Bouldin index, DBI)[3]衡量每个聚类与其最相似的聚类之间的平均相似度，其中相似度定义为聚类内距离(聚类中点到聚类中心的距离)与聚类间距离(聚类中心之间的距离)之比。

S_i是簇i中所有点到簇c ᵢ 质心的平均距离

S_i衡量簇的“扩散”或“大小”。D (c_i，c_j)是簇I和j的质心之间的距离。

比值(S_i+ S_j)/ d(c_i，c_j)表示聚类i和聚类j之间的相似度，即聚类之间的距离和重叠程度。当两个簇都“大”(即具有较大的内部距离)时，分子(即两个簇的扩散之和)就很高。当簇彼此靠近时，表示簇质心之间距离的分母较低。因此，如果分子和分母之间的比例较大，则两个簇可能重叠或分离不好。相反如果比例很小，则表明簇相对于它们的大小是分开的。

对于每一个聚类 i，DB值确定最大这个比率的聚类 j，即与聚类 i 最相似的聚类。最终的DB值是所有聚类的这些最坏情况相似度的平均值。

因此，DB值越低，表明簇越紧凑且分离良好，其中0是可能的最低值。

在Scikit-Learn中可以使用函数sklearn.metrics.davies_bouldin_score()来计算。

 from sklearn.metrics import davies_bouldin_score
 
 print(f'BD(2 clusters): {davies_bouldin_score(X, labels_k2):.3f}')
 print(f'BD(3 clusters): {davies_bouldin_score(X, labels_k3):.3f}')
 print(f'BD(4 clusters): {davies_bouldin_score(X, labels_k4):.3f}')

结果如下：

 BD(2 clusters): 0.633
 BD(3 clusters): 0.480
 BD(4 clusters): 0.800

当k = 3时，DBI得分最低。

优点：

• 易于快速计算。

• 很容易理解。该数值越小表示聚类越好，值为0表示聚类比较理想。

• 和前两个分数一样，它可以用来找到最优的簇数。

缺点：

• 倾向于支持凸簇，对于不同大小或不规则形状的簇可能表现不佳。

• 对于评估基于密度的聚类算法(如DBSCAN)效率较低。

• 噪声和异常值会显著影响指数。

其他内部指标

还有许多其他内部聚类评价方法。参见[2]，详细研究了11种内部度量(包括上面提到的那些)及其在验证不同类型数据集聚类方面的有效性。

外部指标

当数据点的真实标签已知时，则可以使用外部评价指标。这些度量将聚类算法的结果与真值标签进行比较。

1、列联矩阵(contingency matrix）

与分类问题中的混淆矩阵类似，列联矩阵(或表)描述了基本真值标签和聚类标签之间的关系。

矩阵的行表示真类，列表示簇。矩阵中的每个单元格，用 n∈_j表示，包含了类标号为i并分配给聚类j的数据点的个数。

我们可以通过sklearn.metrics.cluster.contingency_matrix()构建列联矩阵。该函数以真值标签和聚类标签作为参数进行评估。

 from sklearn.metrics.cluster import contingency_matrix
 
 true_labels = [0, 0, 0, 1, 1, 1]
 cluster_labels = [0, 0, 1, 1, 2, 2]
 
 contingency_matrix(true_labels, cluster_labels)

结果如下：

 array([[2, 1, 0],
        [0, 1, 2]], dtype=int64)

矩阵表示将两个0类的数据点放置在簇0中，一个点放置在簇1中。将类1中的两个数据点放置在簇2中，将一个数据点放置在簇1中。

很多的外部评价指标，都使用列联矩阵作为其计算的基础，了解了列联矩阵我们开始介绍一些外部指标。

2、Adjusted Rand Index(ARI)

Rand Index (RI)[4]以William Rand命名，通过两两比较来衡量聚类分配与真实类标签之间的相似性。计算簇分配和类标签之间的一致数与总数据点对数的比值：

A是具有相同类标签且属于同一聚类的点对的数目，B是具有不同类标签且属于不同聚类的点对的个数。N是总点数。

RI的范围从0到1，其中1表示簇分配和类标签完全相同。

可以使用sklearn.metrics.rand_score()进行计算。

 from sklearn.metrics import rand_score
 
 true_labels = [0, 0, 0, 1, 1, 1]
 cluster_labels = [0, 0, 1, 1, 2, 2]
 
 print(f'RI = {rand_score(true_labels, cluster_labels):.3f}')

得到：

 RI = 0.667

在我们的这个例子中a = 2, b = 8，因此

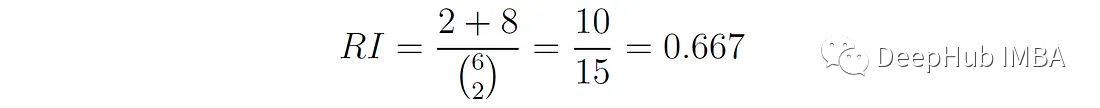
Rand Index的问题是，即使对于随机的簇分配，它也可以得到很高的值，特别是当簇数量很大时。这是因为当聚类数量增加时，随机将不同标签的点分配给不同聚类的概率增加。因此特定的RI值可能是模糊的，因为不清楚分数中有多少是偶然的，多少是实际一致的。

而ARI通过将RI分数标准化来纠正这一点，考虑到随机分配簇时的预期RI分数。计算公式如下：

其中E[RI]为随机聚类分配下Rand指数的期望值。该值是使用上面描述的列联表计算的。我们首先计算表中每行和每列的和：

A_i是属于第i类的点的总数：

B_j是分配给聚类j的总点数:

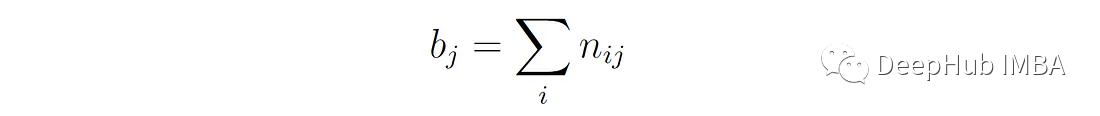
然后使用以下公式计算ARI：

分子表示如果簇分配是随机的(E[RI])，则实际配对Rand指数与预期配对数之间的差值。分母表示最大可能的配对数(最大Rand指数)与随机情况下的期望配对数(E[RI])之差。

规范化此值，调整数据集的大小和元素跨簇的分布。

ARI值的范围从-1到1，其中1表示簇分配和类标签之间完全一致，0表示随机一致，负值表示一致性低于偶然预期。

 from sklearn.metrics import adjusted_rand_score
 
 print(f'ARI = {adjusted_rand_score(true_labels, cluster_labels):.3f}')

结果如下：

 ARI = 0.242

独立于类标签的聚类赋值会得到ARI比如负值或接近0：

 true_labels = [0, 0, 0, 1, 1, 1]
 cluster_labels = [0, 1, 2, 0, 1, 2]
 
 print(f'RI = {rand_score(true_labels, cluster_labels):.3f}')
 print(f'ARI = {adjusted_rand_score(true_labels, cluster_labels):.3f}')

结果如下：

 RI = 0.400
 ARI = -0.364

使用我们上面创建的数据集，我们数据点有真实标签(存储在y变量中)，所以可以使用外部评估指标来评估我们之前获得的三个k-means聚类。这些聚类的ARI评分如下:

 print(f'ARI(2 clusters): {adjusted_rand_score(y, labels_k2):.3f}')
 print(f'ARI(3 clusters): {adjusted_rand_score(y, labels_k3):.3f}')
 print(f'ARI(4 clusters): {adjusted_rand_score(y, labels_k4):.3f}')

结果如下：

 ARI(2 clusters): 0.565
 ARI(3 clusters): 1.000
 ARI(4 clusters): 0.864

当k = 3时，得到一个完美的ARI分数，这意味着在这种情况下，簇分配和真实标签之间存在完美匹配。

优点：

• RI分数的取值范围是0到1,ARI分数的取值范围是-1到1。有界范围使得比较不同算法之间的分数变得容易。

• 对于任意数量的样本和簇，随机(均匀)簇分配的ARI分数都接近于0。

• ARI对机会的调整使其更加可靠和可解释性。

• 没有对聚类结构做任何假设，这使得这些指标对于比较不同的聚类算法非常有用，而不依赖于聚类形状。

缺点：

• 需要有真实的标签来确定结果

3、同质性、完整性和v测度

这些方法通过检查聚类分配与真实类标签的一致性来评估聚类的质量。

同质性 Homogeneity 度量每个簇是否只包含单个类的成员。

定义如下：

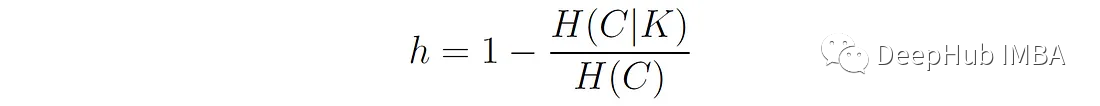
这里：

C代表真值类标签。K表示算法分配的聚类标签。H(C|K)是给定聚类分配的类分布的条件熵的加权平均值：

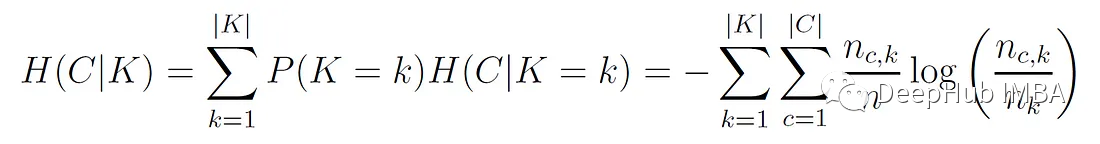
其中nc，_k为分配给k簇的c类样本数，n_k为k簇的样本数，n为总样本数。H(C)为类分布的熵：

同质性评分范围为0 ~ 1，其中1表示完全同质性，即每个簇只包含单个类的成员。

完整性 Completeness 度量给定类的所有成员是否被分配到同一个簇。

定义如下：

H(K|C)是给定类标签的聚类分布条件熵的加权平均值：

其中nc为c类的样本数。

H(K)为聚类分布的熵：

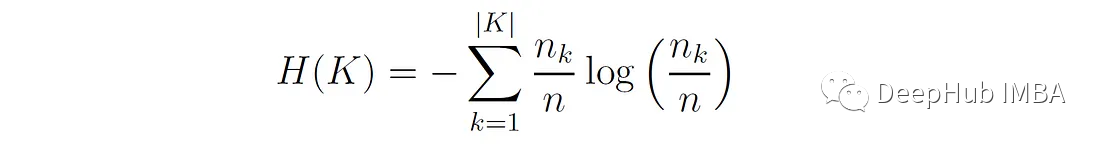
与同质性一样，完整性的范围从0到1，其中1表示完全完整，即每个类成员被分配到单个簇。

V-measure是同质性和完备性的调和平均值，

它可以提供一个单一的分数来评估聚类性能：

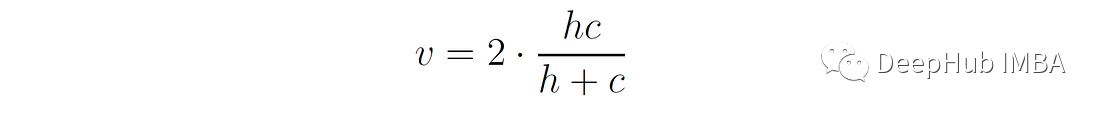
通过使用调和均值，V-measure惩罚同质性和完整性之间的不平衡，鼓励更均匀的聚类性能。

在Scikit-Learn中可以使用sklearn.metrics中的函数homogeneity_score、completeness_score和v_measure_score来计算

 from sklearn.metrics import homogeneity_score, completeness_score, v_measure_score
 
 true_labels = [0, 0, 0, 1, 1, 1]
 cluster_labels = [0, 0, 1, 1, 2, 2]
 
 print(f'Homogeneity = {homogeneity_score(true_labels, cluster_labels):.3f}')
 print(f'Completeness = {completeness_score(true_labels, cluster_labels):.3f}')
 print(f'V-measure = {v_measure_score(true_labels, cluster_labels):.3f}')

结果如下：

 Homogeneity = 0.667
 Completeness = 0.421
 V-measure = 0.516

将其应用在我们的示例上：

print(f'V-measure(2 clusters): {v_measure_score(y, labels_k2):.3f}')
 print(f'V-measure(3 clusters): {v_measure_score(y, labels_k3):.3f}')
 print(f'V-measure(4 clusters): {v_measure_score(y, labels_k4):.3f}')

结果如下：

 V-measure(2 clusters): 0.711
 V-measure(3 clusters): 1.000
 V-measure(4 clusters): 0.895

当k = 3时，我们得到一个完美的V-measure分数1.0，这意味着聚类标签与基本真值标签完全一致。

优点：

• 提供簇分配和类标签之间匹配的直接评估。

• 比分在0到1之间，有直观的解释。

• 没有对簇结构做任何假设。

缺点：

• 不要考虑数据点在每个簇中的分布情况。

• 不针对随机分组进行规范化(不像ARI)。这意味着取决于样本、簇和类的数量，样本的完全随机分组并不总是产生相同的同质性、完备性和v度量值。因此，对于小数据集(样本数量< 1000)或大量簇(> 10)，使用ARI更安全。

4、Fowlkes-Mallows Index（FMI）

Fowlkes-Mallows Index (FMI)[5]定义为对精度(分组点对的准确性)和召回率(正确分组在一起的对的完整性)的几何平均值：

TP(True Positive)是具有相同类标签并属于同一簇的点对的数量。FP (False Positive)是具有不同类标签但被分配到同一聚类的点对的数量。FN(False Negative)是具有相同类标签但分配给不同簇的点对的数量。

FMI评分范围为0 ~ 1，其中0表示聚类结果与真实标签不相关，1表示完全相关。

Scikit-Learn中可以使用函数sklearn.metrics. fowlkes_malallows_score()来计算这个分数

 from sklearn.metrics import fowlkes_mallows_score
 
 true_labels = [0, 0, 0, 1, 1, 1]
 cluster_labels = [0, 0, 1, 1, 2, 2]
 
 print(f'FMI = {fowlkes_mallows_score(true_labels, cluster_labels):.3f}')

结果：FMI = 0.471，在本例中，TP = 2, FP = 1, FN = 4，则：

将其应用到我们的示例：

 print(f'FMI(2 clusters): {v_measure_score(y, labels_k2):.3f}')
 print(f'FMI(3 clusters): {v_measure_score(y, labels_k3):.3f}')
 print(f'FMI(4 clusters): {v_measure_score(y, labels_k4):.3f}')

结果如下：

 FMI(2 clusters): 0.711
 FMI(3 clusters): 1.000
 FMI(4 clusters): 0.895

当k = 3时，得到了一个完美的FMI分数，这表明聚类分配与基本真值标签完全一致。

优点：

• 同时考虑准确率和召回率，提供一个平衡的聚类性能视图。

• 比分在0到1之间。

• 对于任意数量的样本和簇，随机(均匀)标签分配的FMI得分接近于0。

• 不对簇结构做假设。

缺点：

• 它是基于对元素的分析，这可能无法捕捉到簇更广泛的结构特性，比如它们的形状或分布。

• 当数据集高度不平衡(即一个类主导数据集)时，FMI可能无法准确反映聚类的有效性。

总结

下表总结了本文讨论的不同指标和特点：