纹理的另一种常见的应用就是凹凸映射。凹凸映射的目的是使用一张纹理来修改模型表面的法线,以便为模型提供更多的细节。这种方法不会真的改变模型的顶点位置,只是让模型看起来好像是“凹凸不平”的,但可以从模型的轮廓看出“破绽”。
有两种主要的方法可以用来进行凹凸映射:一种方法是使用一张高度纹理(height map)来模拟表面位移,然后得到一个修改后的法线值,这种方法又被称为高度映射;另一种方法则是使用一张法线纹理来直接存储表面法线,这种方法又被称为法线映射(normal mapping)。尽管我们常常将凹凸映射和法线映射当成是相同的技术,但我们需要知道它们之间的不同。
一、高度纹理
首先看第一种技术,即使用一张高度图来实现凹凸映射。高度图中存储的是强度值(intensity),它用于表示模型表面局部的海拔高度。因此颜色越浅表明该位置的表面法线越向外凸起,而颜色越深表明该位置越向里凹。这种方法好处是非常直观,我们可以从高度图中明确地知道一个模型表面的凹凸情况,但缺点是计算更加复杂,在实时计算时不能直接得到表面法线,而是需要由像素的灰度值计算而得,因此需要消耗更多的性能。
高度图通常会和法线映射一起使用,用于给出表面凹凸的额外信息。也就是说我们通常会使用法线映射来修改光照。
二、法线纹理
而法线纹理中存储的就是表面的法线方向。由于法线方向的分量范围在[-1,1],而像素的分量范围为[0,1],因此我们需要做一个映射,通常使用的映射就是:
pixel=(normal+1)/2;
这就要求,我们在shader中对法线纹理进行采样后,还需要对结果进行一次反映射的过程,以得到原先的法线方向。反映射的过程实际上就是使用上面映射函数的逆函数:
normal=pixel*2-1;
然而,由于方向是相对于坐标空间来说的,那么法线纹理中存储的法线方向在哪个坐标空间中呢?对于模型顶点自带的法线,它们是定义在模型空间中的,因此一种直接的想法就是将修改后的模型空间中的表面法线存储在一张纹理中,这种纹理被称为模型空间中的法线纹理。然而在实际制作中,我们往往采用另一种坐标空间,即模型顶点的切线空间来存储法线,对于模型的每个顶点,都有一个属性自己的切线空间,这个切线空间的原点就是该顶点本身,而z轴是顶点的法线方向n,x轴是顶点的切线方向t,而y轴可由法线和切线叉积而得,也被称为副切线或副法线。
如下图:
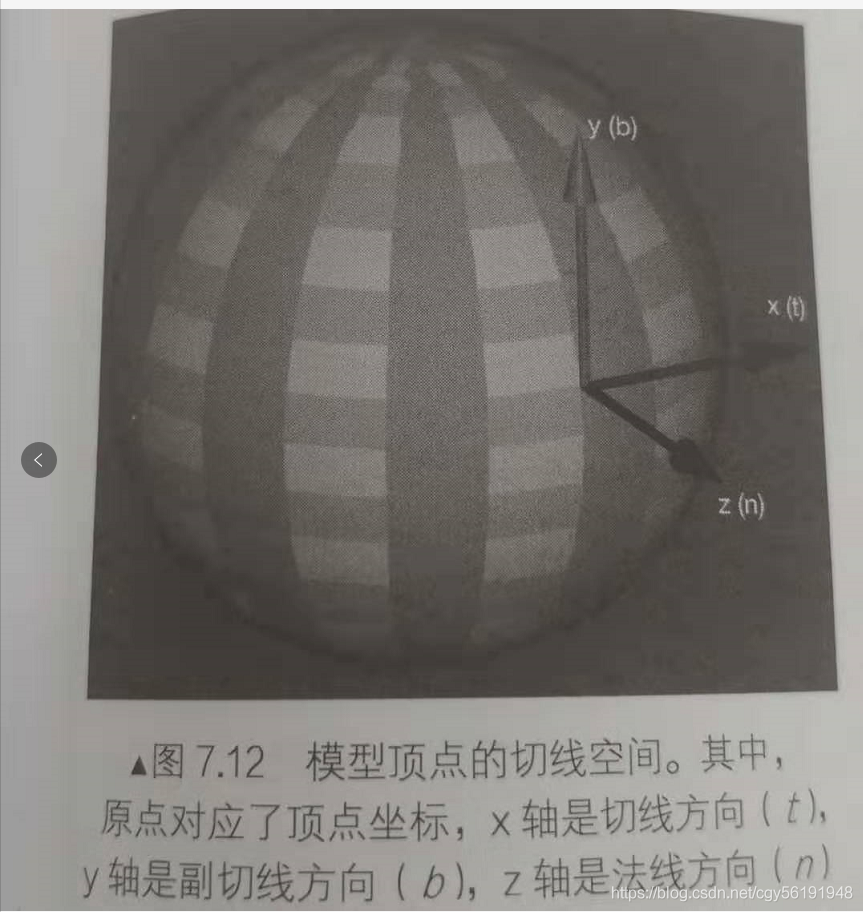
这种纹理被称为切线空间的法线纹理,下图分别给出了模型空间和切线空间下的法线纹理:
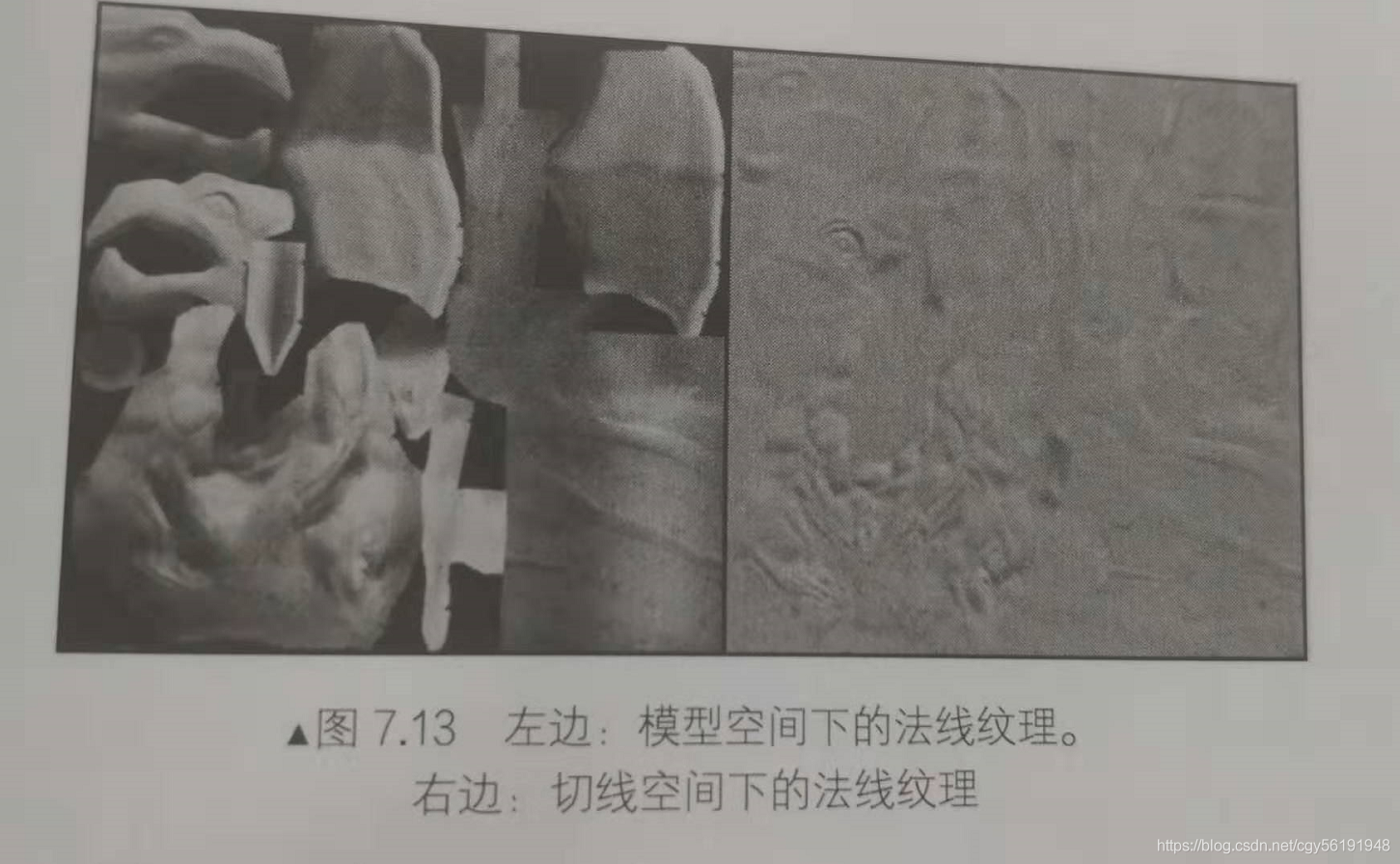
从图中可以看出, 模型空间下的法线纹理看起来是五颜六色的,这是因为所有法线所在的坐标空间是同一个坐标空间,即模型空间,而每个点存储的法线方向是各异的,有的是(0,1,0),经过映射后存储到纹理中就对应了RGB(0.5,1,0.5)浅绿色,有的是(0,-1.0),经过映射后存储到纹理中就对应了(0.5,0,0.5)紫色。而切线空间下的法线纹理看起来几乎全是浅蓝色的。这是因为每个法线方向所在的坐标空间是不一样的,即表面每点各自的切线空间。这种法线纹理其实就是存储了每个点在各种的切线空间中的法线扰动方向。也就是说,如果一个点的法线方向不变,那么在它的切线空间中,新的法线方向就是z轴方向,即值为(0,0,1),经过映射后存储在纹理中就对应了RGB(0.5,0.5,1)浅蓝色。而这个颜色就是法线纹理中大片的蓝色,这些蓝色实际上说明顶点的大部分法线是和模型本身的法线一样的,不需要改变。
总体来说,模型空间下的法线纹理更符合人类的直观认识,而且法线纹理本身也很直观,容易调整,因为不同的法线代表了不同的颜色。但美术人员往往更喜欢使用切线空间下的法线纹理,那么这是为什么呢?
实际上法线本身存储在哪个坐标系都是可以的,我们甚至可以选择存储在世界空间下。但问题是我们并不是单纯的想要得到法线,后续的光照计算才是我们的目的。而选择哪个坐标系意味着我们需要把不同信息转换到相应坐标系中。例如如果选择了切线空间,我们需要把从法线纹理中得到的法线方向从切线空间转换到世界空间(或其他空间)中。
总体来说,使用模型空间来存储法线的优点如下:
1. 实现简单,更加直观。我们甚至都不需要模型原始法线和切线等信息,也就是说计算更少。生成它也非常简单,而如果要生成切线空间下法线纹理,由于模型的切线一般是和uv方向相同,因此想要得到效果比较好的法线映射就要求纹理映射也是连续的。
2. 在纹理坐标的缝合处和尖锐的边角部分,可见的突变(缝隙)较少,既可以提供平滑的边界。这是因为模型空间下的法线纹理存储的是同一坐标系下的法线信息,因此在边界处通过插值得到的法线可以平滑变换。而在切线空间下的法线纹理中的法线信息是依靠纹理坐标的方向得到的结果,可能会在边缘处或尖锐的部分造成更多可见的缝合迹象。
但使用切线空间有很多优点:
自由度很高。模型空间下的法线纹理记录的是绝对法线信息,仅可用于创建它时的那个模型,而应用到其他模型上效果就完全错误了。而切线空间下的法线纹理记录的是相对法线信息,意味着即便把纹理应用到一个完全不同的网格上,也可以得到一个合理的结果。
可进行uv动画。比如我们可以移动一个纹理的UV坐标来实现一个凹凸移动的效果,但使用模型空间下的法线纹理会得到完全错误的结果。原因同上,这种uv动画在水或者火山这种类型的物体上经常会用到。
可压缩。由于切线空间下的法线纹理中法线的Z方向总是正方向,因此我们可以仅存储XY方向,而推导得到Z方向。而模型空间下纹理的每个方向都是可能的,因此必须要存储3个方向的值,不可压缩。
切线空间下的法线纹理的前两个优点足以让很多人放弃模型空间下的法线纹理而选择它,从上面的优点可以看出,切线空间在很多情况下都优于模型空间,而且可以节省美术人员的工作。因此在一般项目中,我们使用的也是切线空间下的法线纹理。
三、实践
我们需要在计算光照模型中统一各个方向矢量所在的坐标空间,由于法线纹理中存储的法线是切线空间下的方向,因此通常我们有两种选择:一种选择是在切线空间下进行光照计算,此时我们需要把光照方向、视角方向变换到切线空间下;另一种选择是在世界空间下进行光照计算,此时我们需要把采样得到的法线方向变换到世界空间下,再和世界空间下的光照方向和视角方向进行计算。从效率上来讲,第一种方法往往要优于第二种方法,因为我们可以在顶点着色器中就完成光照方向和视角方向的变换。而第二种方法由于要先对法线纹理进行采样,所以变换过程必须在片元着色器中实现,这意味着我们需要在片元着色器中进行一次矩阵操作。但从通用性角度来说,第二种方法要优于第一种方法,因为有时我们需要在世界空间下进行一些计算,例如在cubemap进行环境映射时,我们需要使用世界空间下的反射方向对cubemap进行采样。如果同时需要进行法线映射,我们就需要把法线方向变换到世界空间下。当然也可以选择其他坐标空间进行计算,但切线空间和世界空间是最为常用的两种空间。
3.1 在切线空间下计算
在切线空间下计算光照模型基本思路:在片元着色器通过纹理采样得到切线空间下的法线,然后再与切线空间下的视角方向、光照方向进行计算,得到最终的光照结果。为此我们首先需要在顶点着色器中视角方向和光照方向从模型空间变换到切线空间中,即我们需要知道从模型空间到切线空间的变换矩阵,这个变换矩阵的逆矩阵,即从切线空间到模型空间的变换矩阵很好得到,我们在顶点着色器中按切线(x轴)、副切线(y轴)、法线(z轴)的顺序按列排列即可。之前的理论知识讲过,如果一个变换中仅存在平移和旋转变换,那么这个变换的逆矩阵等于它的转置矩阵,而从切线空间到模型空间的变换正是符合这样的要求的变换。因此从模型空间到切线空间的变换矩阵就是从切线空间到模型空间的变换矩阵的转置矩阵,我们把切线(x轴)、副切线(y轴)、法线(z轴)的顺序按行排列即可得到。
效果图如下:

1. 在Properties语义块中添加了法线纹理的属性,以及用于控制凹凸程度的属性:
Properties {
_Color ("Color Tint", Color) = (1, 1, 1, 1)
_MainTex ("Main Tex", 2D) = "white" {}
_BumpMap ("Normal Map", 2D) = "bump" {}
_BumpScale ("Bump Scale", Float) = 1.0
_Specular ("Specular", Color) = (1, 1, 1, 1)
_Gloss ("Gloss", Range(8.0, 256)) = 20
}对于法线纹理BumpMap,我们使用"bump"作为它的默认值,"bump"是unity内置的法线纹理,当没有提供任何法线纹理时,"bump"就对应了模型自带的法线信息。_BumpScale则是用于控制凹凸程度的,当它为0时,意味着该法线纹理不会对光照产生任何影响。
2. 定义光照模式、指令、上面属性对应的变量:
SubShader {
Pass {
Tags { "LightMode"="ForwardBase" }
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "Lighting.cginc"
fixed4 _Color;
sampler2D _MainTex;
float4 _MainTex_ST;
sampler2D _BumpMap;
float4 _BumpMap_ST;
float _BumpScale;
fixed4 _Specular;
float _Gloss;为了得到该纹理的属性(平铺和偏移系数),我们为_MainTex和_BumpMap定义了_MainTex_ST和_BumpMap_ST变量。
3. 切线空间是由顶点法线和切线构建出的一个坐标空间,因此我们需要得到顶点的切线信息,为此我们修改顶点着色器的输入结构体av2:
struct a2v {
float4 vertex : POSITION;
float3 normal : NORMAL;
float4 tangent : TANGENT;
float4 texcoord : TEXCOORD0;
};我们使用TANGENT语义来描述float4类型的tangent变量,以告诉unity把顶点的切线方向方向填充到tangent变量中,和法线方向不同,tangent类型是float4,这是因为我们需要使用tangent.w变量来决定切线空间中的第三个坐标轴——副切线的方向性。
4. 我们需要在顶点着色器计算切线空间下的光照和视角方向,因此我们在v2f结构体中添加了两个变量来存储变换后的光照和视角方向:
struct v2f {
float4 pos : SV_POSITION;
float4 uv : TEXCOORD0;
float3 lightDir: TEXCOORD1;
float3 viewDir : TEXCOORD2;
};5. 定义顶点着色器
v2f vert(a2v v) {
v2f o;
o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
o.uv.xy = v.texcoord.xy * _MainTex_ST.xy + _MainTex_ST.zw;
o.uv.zw = v.texcoord.xy * _BumpMap_ST.xy + _BumpMap_ST.zw;
///
/// Note that the code below can handle both uniform and non-uniform scales
///
// Construct a matrix that transforms a point/vector from tangent space to world space
fixed3 worldNormal = UnityObjectToWorldNormal(v.normal);
fixed3 worldTangent = UnityObjectToWorldDir(v.tangent.xyz);
fixed3 worldBinormal = cross(worldNormal, worldTangent) * v.tangent.w;
/*
float4x4 tangentToWorld = float4x4(worldTangent.x, worldBinormal.x, worldNormal.x, 0.0,
worldTangent.y, worldBinormal.y, worldNormal.y, 0.0,
worldTangent.z, worldBinormal.z, worldNormal.z, 0.0,
0.0, 0.0, 0.0, 1.0);
// The matrix that transforms from world space to tangent space is inverse of tangentToWorld
float3x3 worldToTangent = inverse(tangentToWorld);
*/
//wToT = the inverse of tToW = the transpose of tToW as long as tToW is an orthogonal matrix.
float3x3 worldToTangent = float3x3(worldTangent, worldBinormal, worldNormal);
// Transform the light and view dir from world space to tangent space
o.lightDir = mul(worldToTangent, WorldSpaceLightDir(v.vertex));
o.viewDir = mul(worldToTangent, WorldSpaceViewDir(v.vertex));
///
/// Note that the code below can only handle uniform scales, not including non-uniform scales
///
// Compute the binormal
// float3 binormal = cross( normalize(v.normal), normalize(v.tangent.xyz) ) * v.tangent.w;
// // Construct a matrix which transform vectors from object space to tangent space
// float3x3 rotation = float3x3(v.tangent.xyz, binormal, v.normal);
// Or just use the built-in macro
// TANGENT_SPACE_ROTATION;
//
// // Transform the light direction from object space to tangent space
// o.lightDir = mul(rotation, normalize(ObjSpaceLightDir(v.vertex))).xyz;
// // Transform the view direction from object space to tangent space
// o.viewDir = mul(rotation, normalize(ObjSpaceViewDir(v.vertex))).xyz;
return o;
}由于我们使用了两张纹理,因此需要存储两个纹理坐标。为此我们把v2f的uv变量的类型定义为float4变量,其中xy分量存储了_MainTex的纹理坐标,而zw分量存储了_BumpMap的纹理坐标(实际上,_MainTex和_BumpMap通常会使用同一组纹理坐标,出于减少插值寄存器的数目的目的,我们往往只计算和存储一个纹理坐标即可)。然后我们把模型空间下切线方向、副切线方向和法线方向按行排列来得到从模型空间到切线空间的变换矩阵rotation。需要注意,在计算副切线时我们使用v.tangent.w和叉积结果进行相乘,这是因为和切线与法线方向都垂直的方向有两个,而w决定了我们选择其中哪一个方向。而w决定了我们选择其中哪一个方向。untiy也提供了一个内置宏TANGENT_SPACE_ROTATION(在unityCG.cginc中被定义)来帮助我们直接计算得到rotation变换矩阵,它的实现和上述代码完全一样。然后使用unity内置函数ObjSpaceLightDir和ObjSpaceViewDir来得到模型空间下的光照和视角方向,再利用变换矩阵rotation把他们从模型空间变换到切线空间。
6. 由于我们在顶点着色器完成了大部分工作,因此片元着色器中只需要采样得到切线空间下的法线方向,在切线空间下进行光照即可。
fixed4 frag(v2f i) : SV_Target {
fixed3 tangentLightDir = normalize(i.lightDir);
fixed3 tangentViewDir = normalize(i.viewDir);
// Get the texel in the normal map
fixed4 packedNormal = tex2D(_BumpMap, i.uv.zw);
fixed3 tangentNormal;
// If the texture is not marked as "Normal map"
// tangentNormal.xy = (packedNormal.xy * 2 - 1) * _BumpScale;
// tangentNormal.z = sqrt(1.0 - saturate(dot(tangentNormal.xy, tangentNormal.xy)));
// Or mark the texture as "Normal map", and use the built-in funciton
tangentNormal = UnpackNormal(packedNormal);
tangentNormal.xy *= _BumpScale;
tangentNormal.z = sqrt(1.0 - saturate(dot(tangentNormal.xy, tangentNormal.xy)));
fixed3 albedo = tex2D(_MainTex, i.uv).rgb * _Color.rgb;
fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz * albedo;
fixed3 diffuse = _LightColor0.rgb * albedo * max(0, dot(tangentNormal, tangentLightDir));
fixed3 halfDir = normalize(tangentLightDir + tangentViewDir);
fixed3 specular = _LightColor0.rgb * _Specular.rgb * pow(max(0, dot(tangentNormal, halfDir)), _Gloss);
return fixed4(ambient + diffuse + specular, 1.0);
}上面代码中,我们首先利用tex2D对法线纹理_BumpMap进行采样,如之前所示,法线纹理中存储的是把法线经过映射后得到的像素值,因此我们需要把它们反映射回来,如果我们没有在untiy里把该法线纹理的类型设置成NormalMap,就需要在代码中手动进行这个过程,我们首先把packedNormal的xy分量按之前提到的公式映射回法线方向,然后乘以_BumpScale(控制凹凸程度)来得到tangentNormal的xy分量。由于法线都是单位矢量,因此tangentNormal.z分量可以由tangentNormal.xy计算而得。由于我们使用的是切线空间下的法线纹理,因此可以保证法线方向的z分量为正。在unity中,为了方便unity对法线纹理的存储进行优化,我们通常会把法线纹理的类型标识成Normal map,unity会根据平台来选择不同的压缩方法。这时我们再使用上面的方法来计算就会得到错误的结果,因为此时_BumpMap的rgb分量并不再是切线空间下的法线方向的xyz值了,后面具体解释,这种情况下可以使用Unity内置函数UnpackNormal来得到正确的法线方向。
3.2 在世界空间下计算
现在实现第二种方法,即在世界空间下计算光照模型。我们需要在片元着色器中把法线方向从切线空间变换到世界空间下。这种方法的基本思想:在顶点着色器中计算从切线空间到世界空间的变换矩阵,并把它传递给片元着色器。变换矩阵的计算可以由顶点的切线、副切线和法线在世界空间下的表示来得到。最后我们只需要在片元着色器中把法线纹理中的法线方向从切线空间变换到世界空间下即可。尽管这种方法需要更多的计算,但需要使用cubemap进行环境映射的情况下,我们就需要使用这种方法。
1. 需要修改顶点着色器的输出结构体v2f,使它包含从切线空间到世界空间的变换矩阵:
struct v2f {
float4 pos : SV_POSITION;
float4 uv : TEXCOORD0;
float4 TtoW0 : TEXCOORD1;
float4 TtoW1 : TEXCOORD2;
float4 TtoW2 : TEXCOORD3;
};一个插值寄存器最多只能存储float4大小的变量,对于矩阵这样的变量,我们可以把他们拆成度过变量再进行存储。上面代码中的TtoW0、TtoW1和TtoW2就依次存储了从切线空间到世界空间的变换矩阵的每一行。实际上对方向矢量的变换只需要使用3X3大小的矩阵。也就是说,每一行只需要使用float3类型的变量即可。但为了充分利用插值寄存器的存储空间,我们把世界空间下的顶点位置存储在这些变量的w分量中。
2. 修改顶点着色器,计算从切线空间到世界空间的变换矩阵:
v2f vert(a2v v) {
v2f o;
o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
o.uv.xy = v.texcoord.xy * _MainTex_ST.xy + _MainTex_ST.zw;
o.uv.zw = v.texcoord.xy * _BumpMap_ST.xy + _BumpMap_ST.zw;
float3 worldPos = mul(unity_ObjectToWorld, v.vertex).xyz;
fixed3 worldNormal = UnityObjectToWorldNormal(v.normal);
fixed3 worldTangent = UnityObjectToWorldDir(v.tangent.xyz);
fixed3 worldBinormal = cross(worldNormal, worldTangent) * v.tangent.w;
// Compute the matrix that transform directions from tangent space to world space
// Put the world position in w component for optimization
o.TtoW0 = float4(worldTangent.x, worldBinormal.x, worldNormal.x, worldPos.x);
o.TtoW1 = float4(worldTangent.y, worldBinormal.y, worldNormal.y, worldPos.y);
o.TtoW2 = float4(worldTangent.z, worldBinormal.z, worldNormal.z, worldPos.z);
return o;
}在上面代码中,我们计算了世界空间下的顶点切线、副切线和法线的矢量表示,并把他们按列摆放得到从切线空间到世界空间的变换矩阵。我们该矩阵的每一行分别存储在TtoW0、TtoW1和TtoW2中,并把世界空间下的顶点位置的xyz分量分别存储在了这些变量的w分量中,以便充分利用插值寄存器的存储空间。
3. 修改片元着色器,在世界空间下进行光照计算:
fixed4 frag(v2f i) : SV_Target {
// Get the position in world space
float3 worldPos = float3(i.TtoW0.w, i.TtoW1.w, i.TtoW2.w);
// Compute the light and view dir in world space
fixed3 lightDir = normalize(UnityWorldSpaceLightDir(worldPos));
fixed3 viewDir = normalize(UnityWorldSpaceViewDir(worldPos));
// Get the normal in tangent space
fixed3 bump = UnpackNormal(tex2D(_BumpMap, i.uv.zw));
bump.xy *= _BumpScale;
bump.z = sqrt(1.0 - saturate(dot(bump.xy, bump.xy)));
// Transform the narmal from tangent space to world space
bump = normalize(half3(dot(i.TtoW0.xyz, bump), dot(i.TtoW1.xyz, bump), dot(i.TtoW2.xyz, bump)));
fixed3 albedo = tex2D(_MainTex, i.uv).rgb * _Color.rgb;
fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz * albedo;
fixed3 diffuse = _LightColor0.rgb * albedo * max(0, dot(bump, lightDir));
fixed3 halfDir = normalize(lightDir + viewDir);
fixed3 specular = _LightColor0.rgb * _Specular.rgb * pow(max(0, dot(bump, halfDir)), _Gloss);
return fixed4(ambient + diffuse + specular, 1.0);
}我们首先从TtoW0、TtoW1和TtoW2的w分量中构建世界空间下的坐标,然后使用内置的UnityWorldSpaceLightDir和UnityWorldSpaceViewDir函数得到世界空间下的光照和视角方向。接着使用内置的UnpackNormal函数对法线纹理进行采样和解码(需要把法线纹理的格式标识成NormalMap),并使用_BumpScale对其进行缩放。最后我们使用TtoW0、TtoW1和TtoW2存储的变换矩阵把法线变换到世界空间下,这是通过使用点乘操作来实现矩阵的每一行和法线相乘来得到的。
从视觉表现上,在切线空间下和世界空间下计算光照几乎没有任何差别。在unity4.x版本中,在不需要使用Cubemap进行环境映射的情况下,内置的unity shader使用的是切线空间来进行法线映射和光照计算。但在unity5.x中,所有内置的unity shader都使用了世界空间来进行光照计算。这也是为什么unity5.x中表面着色器更容易报错,因为他们使用了更多的插值寄存器来存储变换矩阵。
四、unity中的法线纹理类型
前面提到了当把法线纹理的纹理类型标识成Normal map时,可以使用unity的内置函数UnpackNormal来得到正确的法线方向,如下图:
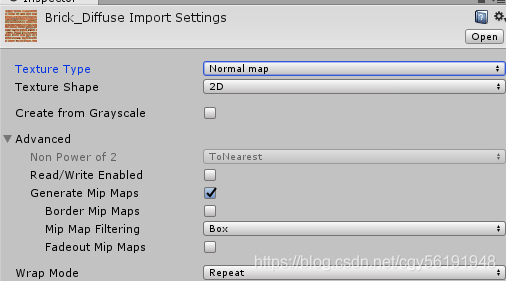
当我们需要使用那些包含了法线映射的内置shader时,必须把使用的法线纹理按照上面的方式标识成Normal map才能得到正确的结果(即便忘了这么做,unity也会在材质面板中国提醒你修正这个问题)这是因为shader都使用了内置的UnpackNormal函数来采样法线方向,那么当我们把纹理类型设置成NormalMap时到底发生了什么?
简单来说,这么做可以让unity根据不同平台对纹理进行压缩(例如使用DX5nm格式),在通过UnpackNormal函数来针对不同的压缩格式对法线纹理进行正确的采样。我们可以在unityCG.cginc里找到UnpackNormal函数的内部实现:
fixed3 UnpackNormalDXT5nm(fixed4 packednormal)
{
fixed3 normal;
normal.xy = packednormal.xy * 2 - 1;
normal.z = sqrt(1 - saturate(dot(normal.xy, normal.xy)));
return normal;
}
inline fixed3 UnpackNormal(fixed4 packednormal)
{
#if defined(UNITY_NO_DXT5nm)
return packednormal.xyz * 2 - 1;
#else
return UnpackNormalDXT5nm(packednormal);
#endif
}从代码中可以看出,在某些平台上由于使用了DXT5nm的压缩格式,因此需要针对这种格式对法线进行解码。在DXT5nm格式的法线纹理中,纹素的a通道(即w分量)对应了法线的x分量,g通道对应了法线的y分量,而纹理的r和b通道则会被舍弃,法线的z分量可以由xy分量推导而得。为什么之前的普通纹理不能按这种方式压缩,而法线就需要使用DXT5nm格式来进行压缩呢?这是因为按我们之前的处理方式,法线纹理被当成一个和普通纹理无异的图,但实际上它只有两个通道是真正必不可少的,因为第三个通道的值可以用另外两个推导出来(法线是单位向量,并且切线空间下的法线方向的z分量始终为正)。使用这种压缩方法就可以减少法线纹理占用的内存空间。
当我们把纹理类型设置成Normal map后,还有一个复选框是Create from Grayscale,这个复选框就是用从高度图生成法线纹理的。高度图本身记录的是相对高度,是一张灰度图,白色表示相对更高,黑色表示相对更低。当我们把一张高度图导入unity后,除了需要把它的纹理类型设置成Normal map外,还需要勾选Create from Grayscale,这样就可以把它和切线空间下的法线纹理同等对待了。
当勾选了Create from Grayscale,还多出两个选项——Bumpiness和Filtering。其中Bumpiness用于控制凹凸程度,而Filtering决定我们使用哪种方式来计算凹凸程度,他有两种选项,一种是Smooth,这使得生成后的法线纹理会比较平滑;另一种是Sharp,它会使用Sobel滤波(一种边缘检测时使用的滤波器)来生成法线。Sobel的滤波实现非常简单,只需要在一个3X3的滤波器中计算x和y方向上的导数,然后从中得到法线即可。具体方法是:对于高度图中每个像素,我们考虑它与水平方向和竖直方向上的像素差,把他们的差当成该点对应的法线在x和y方向上的位移,然后使用之前提到的映射函数存储成到法线纹理的r和g分量即可。
版权声明:本文为CSDN博主「小橙子0」的原创文章,
遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:http://blog.csdn.net/cgy56191948/article/details/102607089






