来源:CSDN
博主:naruhina
文章由我们熟悉的一维连续时间信号的卷积逐渐过渡到图像卷积。文章是循序渐进的,希望想要了解的朋友们可以耐心读一读。本人理解有限,如有错误还请指出。
(1)先看连续时间信号的卷积:
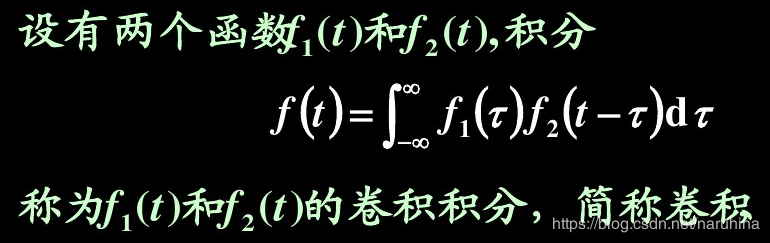
可以看到对与连续时间信号而言,卷积是一种特殊的积分运算,它的过程就是一个函数固定不动,另一个函数先以y轴为对称轴反转,然后不断执行相乘,积分,滑动。
(2.)当我们把连续时间信号离散化后,卷积的定义便成为了:

其中x(n)和h(n)是参与运算的离散时间信号。在这个定义中,卷积的过程尤为清晰:
在坐标轴上让x(n)保持不动,先把h(n)反转,然后不断执行二者重合部分相乘求和然后让h(n)滑动的过程。离散时间信号可以看作是一串序列,它是一维的,如果我们把它扩充为二维序列,那不就是图像了吗?图像的本质就是灰度值的二维序列。
(3.)下面我们来看什么是图像的卷积:
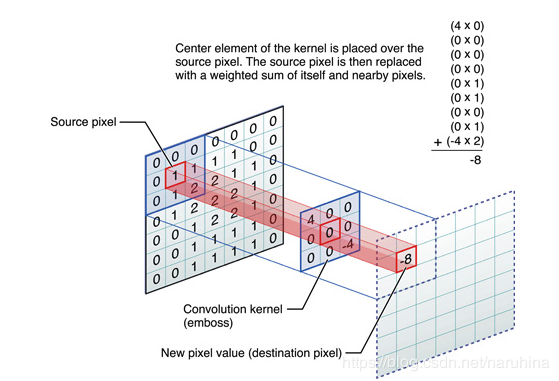
在这幅图中,source pixel 是我们的图像,它本质是灰度的二维序列,图中的convolution kernel是什么呢?这个我们称它为卷积核,这个卷积核就相当于是一维离散信号卷积中的一个参与卷积的信号,图像本身就相当于是一维离散信号卷积中的另一个离散序列信号,图像卷积的过程与一维的情况十分类似:图像卷积就是卷积核在图像上按行滑动遍历像素时不断的相乘求和的过程。举个例子:如图中所示,目前卷积核滑动到了图像左上角,我们把图像上的9个值与卷积核的9个数值按照对应位置相乘再相加得到一个和,这个和就是我们得到的卷积值。然后把卷积核向右移动一个像素,再执行对应位置相乘再相加的过程得到第二个卷积值,当把所有像素遍历完成之后我们得到的结果就构成了一幅图像。这就是卷积得到的图像。
(4)在图像处理中,我们不会为了卷积而去卷积,为什么呢?按照卷积的定义,它是与卷积核相乘求和的结果,如果图像本身像素的数据类型是8位无符号数,那么它的灰度范围就是0(黑色)到255(白色),这样以来相乘后的值很容易大于255,那么怎么办呢?一般就是截断为255。从我这几行的描述可以看到,单单卷积确实没什么用,因为图像卷积的用武之处不在于此。
(5)图像卷积常常用于图像滤波(平滑化),图像梯度,开运算,闭运算,黑帽运算,顶帽运算等形态处理,以及基于梯度运算的边缘提取中。
比如均值滤波的卷积核是这样的:
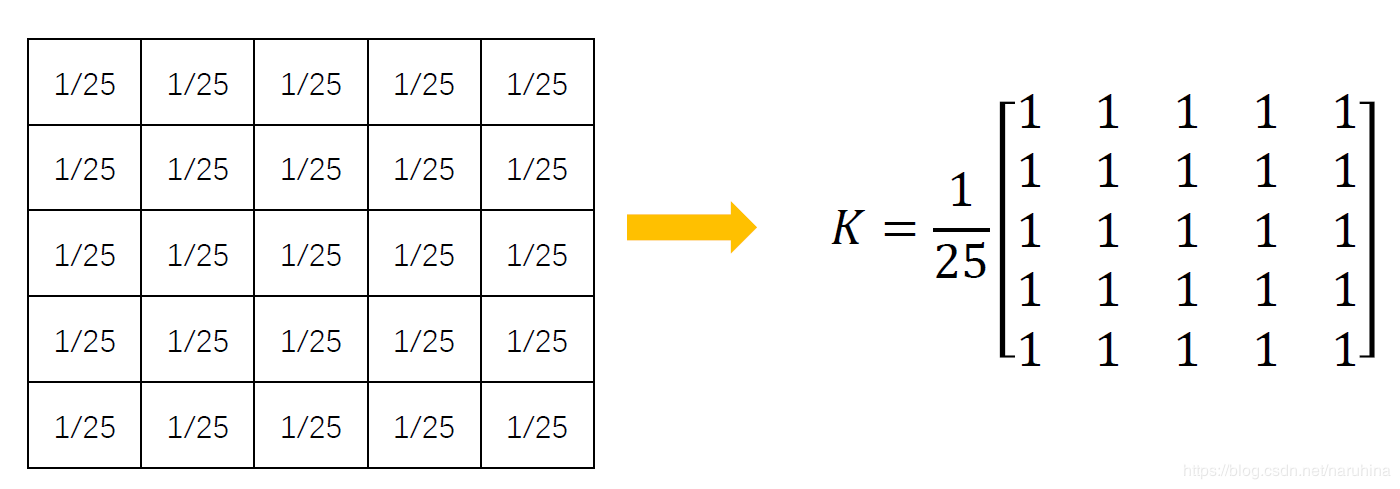
它也是按照卷积运算的过程相乘求和再滑动,只不过它的核里每个值都是1,在求和之后还除以核的大小来取平均。
比如高斯滤波是这样的:
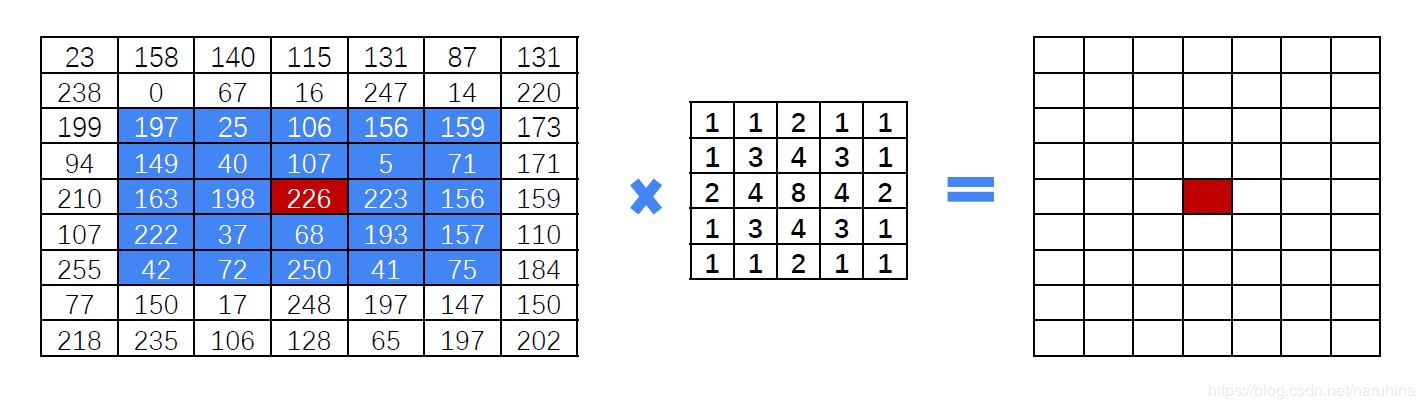
高斯滤波的时候它的核是离中心越近值越大,也就是不同位置的权重不同。在相乘求和之后会除以核内数值的求和值以保证灰度值不会超出范围
看到这里大家应该会有疑惑,不是正在说卷积吗,怎么就开始扯滤波了?情况是这样的:什么是滤波?它的本质就是卷积,是按照一定的特殊规则去卷积,此时使用的卷积核不是随意的,而是有既定的规矩的,比如卷积核应取3x3,5x5这样的具有中心的核,而且核内数值的分布也是有规定的,视不同的滤波方式而定。
讲了这么多我还没有说什么是卷积核,卷积核就是一种求和的规则,是一种映射的规则。原图像像素点的值与对应位置上的卷积核的值相乘然后按权重相加处理,这个过程用数学去表示不就是src(原图像) x kernel(映射规则)=result(卷积的结果) 吗?所以卷积核就是一种运算的规则,由卷积核规则的不同衍生出了不同的滤波方式,不同的梯度运算方式等。
讲到这里我还想再说一说滤波,为什么卷积一下就滤波了呢?我举个例子:就比如上文写到的均值滤波,它的映射规则(就是卷积核)不就是全部都是1除以核大小吗?也就是说原图像与这样的卷积核卷积的结果就是原图像的像素值乘以卷积核对应位置的值相加,很巧合的是核内的值都是1/25(这是对于5x5大小的核来说的),那这样看很显然,卷积的结果就是把原图像像素值相加取平均值。这样一来像素与像素之间的差异性就变小了,图像中分明的线条和边界就是像素值迥然的差异所导致的,差异性减小导致边界就模糊了,图像自然就变得平滑了。说到这里还是没说滤波这个概念,我们在数字信号处理中接触的诸如高通滤波就是为了滤除高频信号(分布在π附近的信号),在图像滤波中也是如此。我刚才说滤波后像素与像素之间的差异性减小了,这不就意味着滤除了高频成分吗?高频信号的定义就是变化很快的信号,在图像中,如果两个像素差异很大就意味着移动一个像素的距离带来的变化就是巨大的,而当这巨大的变化连接起来就是图像中的图形的边界或线条,这样就是为什么线条被称之为高频信号。
我想看到这里大家应该就理解了为什么卷积一下就能滤波了吧,卷积的一种应用形式就是滤波,当然不同的卷积核有不同的卷积效果,所以卷积还有诸如梯度运算等其他的应用形式,差别就在于卷积核的不同
总结起来就是:图像卷积靠卷积核完成,卷积核规定了运算的规则,滤波是卷积运算所带来的效果。不同的卷积核所得到的卷积效果不同,故衍生出了不同种类的滤波,形态运算,梯度运算等等概念。由此可见:卷积是图像处理的基础,许许多多处理方式都是离不开卷积的
如果对梯度运算感兴趣请移步下面这篇博客:
https://blog.csdn.net/naruhina/article/details/104710805
版权声明:本文为CSDN博主「naruhina」的原创文章,
遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/naruhina/article/details/104729037/
