1. 噪声的种类
根据噪声是如何添加进信号中的可以将噪声分为加性噪声和乘性噪声。加性噪声一般指热噪声、散弹噪声等,它们与信号的关系是相加,不管有没有信号,噪声都存在;而乘性噪声一般由信道不理想引起,它们与信号的关系是相乘,信号在它在,信号不在他也就不在。一般通信中把加性随机性看成是系统的背景噪声,而乘性随机性看成系统的时变性(如衰落或者多普勒)或者非线性所造成的。所以两者的另一个显著的区别是,加性噪声是一种线性变化,属于线性时不变的研究范围,而乘性噪声属于一种非线性的变换方式,属于非线性系统。因为非线性系统常常很难建模和求解,所以常常用线性系统来近似非线性系统。这也是为什么《图像复原与重建:图像退化与复原过程模型》只考虑加性噪声的原因。
2. 噪声的主要来源
(1)成象系统的象差、畸变、带宽有限等造成图象失真;
(2)由于成象器件拍摄姿态和扫描非线性引起的图象几何失真;
(3)运动模糊,成象传感器与被拍摄景物之间的相对运动,引起所成图象的运动模糊;
(4)灰度失真,光学系统或成象传感器本身特性不均匀,造成同样亮度景物成象灰度不同;
(5)辐射失真,由于场景能量传输通道中的介质特性如大气湍流效应、大气成分变化引起图象失真;
(6)图象在成象、数字化、采集和处理过程中引入的噪声等。
3. 噪声的空间和频率特性
白噪声(白杂讯),是一种功率频谱密度为常数的随机信号或随机过程,是功率谱密度在整个频域内均匀分布的噪声。此信号在各个频段上的功率是一样的,由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,此信号也因此被称作白噪声。相对的,其他不具有这一性质的噪声信号(功率谱密度不均匀分布)被称为有色噪声。 一般,只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽,并且在该带宽中其频谱密度基本上可以作为常数来考虑,就可以把它作为白噪声来处理。例如,热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度,通常可以认为它们是白噪声。
除了空间周期噪声之外,这里讨论的噪声η(x,y)都是独立于空间坐标,并且噪声与本身不相关(即像素值与噪声值分量的值之间不相关,加性噪声),即认为它是加性白噪声。
4. 一些重要噪声的概率密度函数(PDF)
噪声可以认为是由概率密度函数(PDF)表征的随机变量。下面给是一些重要噪声的概率密度函数。
(1)高斯噪声
高斯噪声在数学上具有已处理性,故实践中常用这种模型,以至于高斯模型常常应用于在一定程度上导致最好结果的场景。高斯随机变量z的PDF如下式

(2)瑞利噪声
瑞利噪声的PDF如下

瑞利噪声的概率密度曲线有两个显著的特点,一个是 a 不在原点处,有一个相对与原点的位移;另一个特点是密度的基本形状向右变形。尤其是第二个特点在噪声参数估计中十分有用。
(3)爱尔兰(伽马)噪声
爱尔兰(伽马)噪声的PDF如下

(4)指数噪声
指数噪声的PDF如下

(5)均匀噪声
均匀噪声的PDF如下
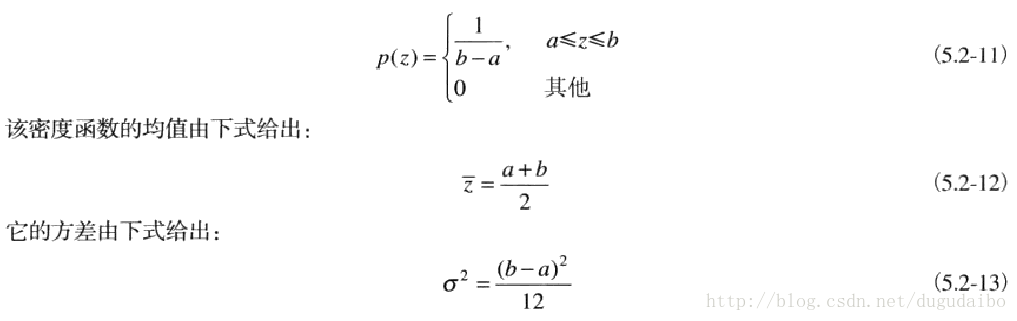
(6)脉冲(椒盐)噪声
脉冲(椒盐)噪声的PDF如下

在图像中 b 和 a 一个是白点,一个是黑点。如果 Pa 和 Pb 中有一个为零,则脉冲噪声称为单脉冲噪声;如果 Pa 和 Pb 均不为 0 且大致相等的时候,脉冲噪声值将类似于在图像上撒上胡椒和盐粒,也正是由于这个原因将这样的噪声称为椒盐噪声。需要注意的是其中由白点构成的是盐粒噪声,而由黑点构成的是胡椒噪声,他们是单脉冲噪声,不是胡椒噪声(胡椒噪声是双脉冲噪声)。
实际上在椒盐噪声中,噪声的值未必都是图像可取值范围中的最大值和最小值。但是与图像信号的强度相比,脉冲污染通常比较大,所以在一幅图像中脉冲噪声通常被数字化为最大值(纯黑或纯白),所以在图像中像椒盐一样出现。

噪声图像及其直方图如下图所示
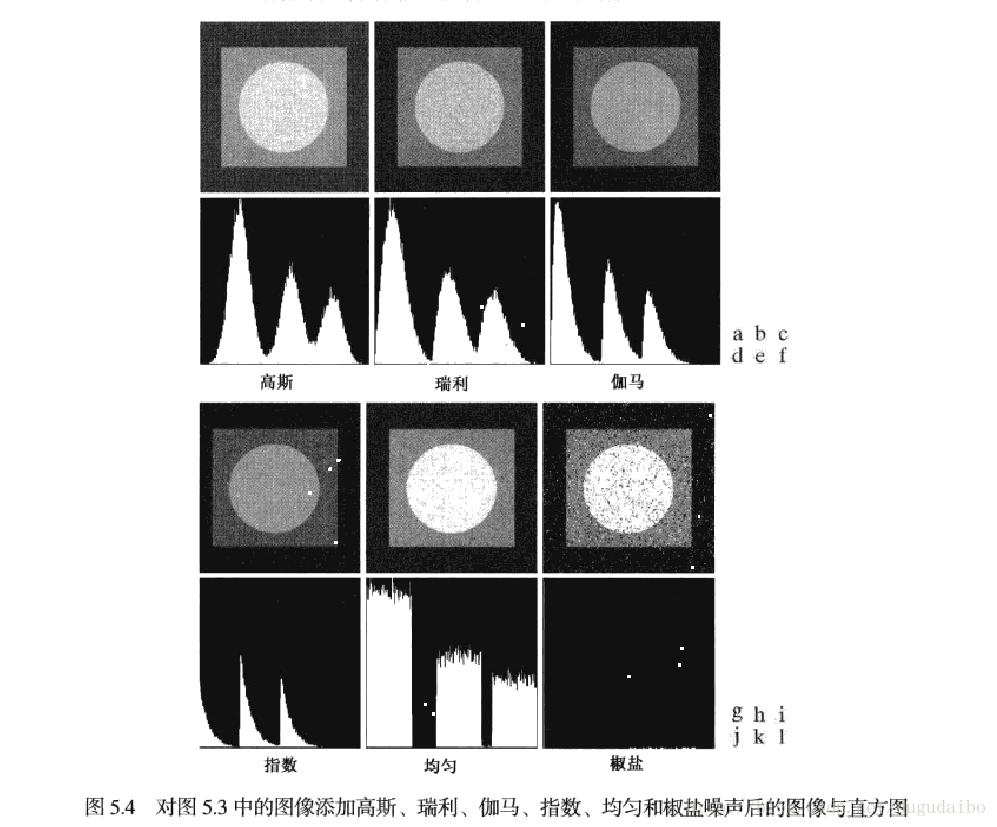
直观来看,前五种噪声很难通被污染的图像本身进行区别,但是椒盐噪声是可以被区分出来的。虽然前五种图像不好区分,但是它们的直方图却很容易区分。所有在后面确定噪声参数的时候,往往首先根据噪声的直方图来确定噪声的种类,再计算该类噪声所对应的参数。
5. 周期噪声

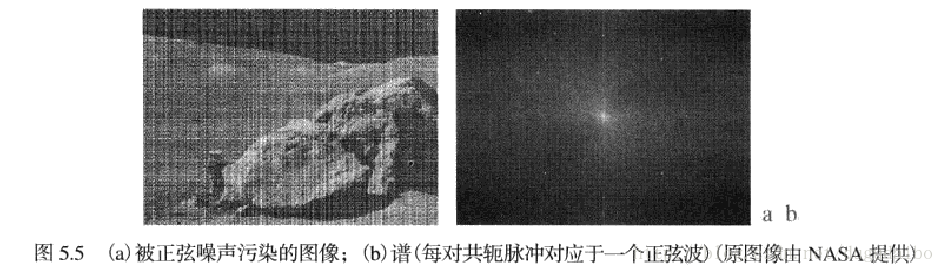
6. 噪声参数估计
周期噪声的参数是通过检查图像的傅里叶频谱来估计的;噪声的PDF参数一般认为可以通过传感器的技术说明得知,但是对于某些特殊装置可能要进行估计,这时常常取灰度值恒定的一部分及逆行分析,如下图所示

即通过直方图的形状首先确定噪声的种类,再通过噪声的均值和方差求解造神的参数。其中椒盐噪声可以不用计算均值方差,直接统计概率即可。
版权声明:本文为CSDN博主「独孤呆博」的原创文章,
遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/dugudaibo/article/details/78387819






