作者:CVPy冰不语
卷积,这个词大家应该都不陌生,数学中傅立叶变换的时候,物理中信号处理的时候,图像处理中滤波的时候、提取边缘的时候,还有深度学习中卷积神经网络的时候,处处可见卷积的影子。卷积在图像处理中的应用非常广泛,可以说理解了卷积,就可以理解图像处理算法的半壁江山,也不知道这个说法是否夸张了。
但是都说卷积卷积,那卷积到底是怎么个卷法呢?本文尝试解答这一问题。
理解的卷积计算过程
想要理解卷积,一些必要的数学公式是少不了的,放心吧,就下面这一个公式了,所有讨论围绕这一个公式展开。
我们从维基百科中对于卷积的解释引入:
设:f(x) , g(x) 是 R 上的两个可积函数,作积分:

可以证明,关于几乎所有的 x∈(-∞,∞) ,上述积分是存在的。这样,随着 x 的不同取值,这个积分就定义了一个新函数 h(x) ,称为函数 f 与 g 的卷积,记为 h(x) = ( f * g )( x ) 。
我们提取下重点公式写在下面,记为公式1:
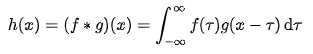
以上公式1最令人迷惑也是最需要注意的部分在于,在等式的左边,自变量是 x ,然而等式的右边自变量却变成了 τ ,更令人疑惑的是——右边自变量不是 x 是 τ 也就算了,竟然还出现了一个 x 。
那么问题来了,x 和 τ ,到底哪个在变?还是两个都在变?如果是都在变,那到底是怎么个变法?
这些问题还是需要慢慢道来。我们先看一个卷积稍微通俗一点的解释。
卷积
(1)即是通过两个函数 f 和 g 生成第三个函数的一种数学算子。
(2)表征函数f与经过翻转和平移的g的乘积函数所围成的的曲边梯形的面积。
上面两句话都非常重要,我们从第二句话开始看,第二句话中包含了以下四个重点信息:
• 翻转
• 平移
• 乘积
• 积分(函数围成的面积不就是积分么?)
我们一个一个来看。先看右边,我们不妨先令 x = x0 , 也就是 x 不变而 τ 变的情况。于是公式1就变成了公式2:
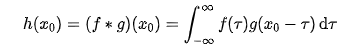
1. 翻转
先看翻转,怎么翻转一个函数呢,想一下最简单的 f(τ) = τ,不难发现, f(τ)翻转之后即为 f(-τ)。我用Python画出了这俩函数的图像,看起来更为直观。

f(x)-f(-x)
2. 平移
然后看一下一个函数如何平移,仍然以 f(τ) = τ为例,回一下我们中学学过的数学知识,也许还能记起来, f( x0 - τ ) = τ就是由 f(-τ) 向右平移 x0 得到的。我们仍然以图说话,用Python作图如下,x0分别取值为20,40,60,80。
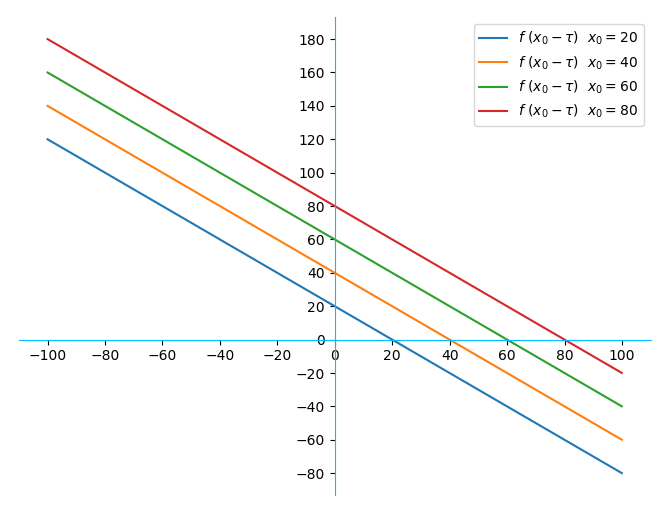
f(t-x)
3. 乘积
现在我们只看公式的右边部分:
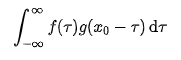
现在我们可以知道 g( x0 - τ )就是 g( τ )翻转之后又向右平移了x0个单位。这时候需要考虑另一个函数 f(τ)了。这里 我们继续举个例子,不妨令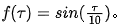 。
。
我们继续用Python画出 f(τ) g( x0 - τ ) 如下图所示:
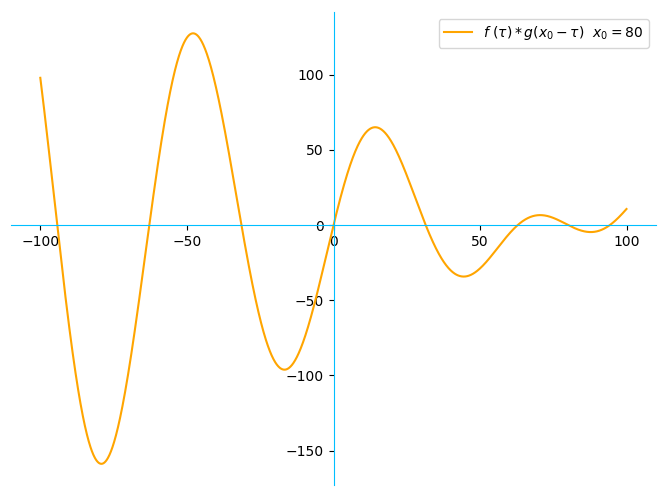
4. 积分
现在是较为完整的公式3的样子了,这里为了能够更好地表达,我们把区间 ( -∞ , ∞ ) 从改为(-50,50),即画出

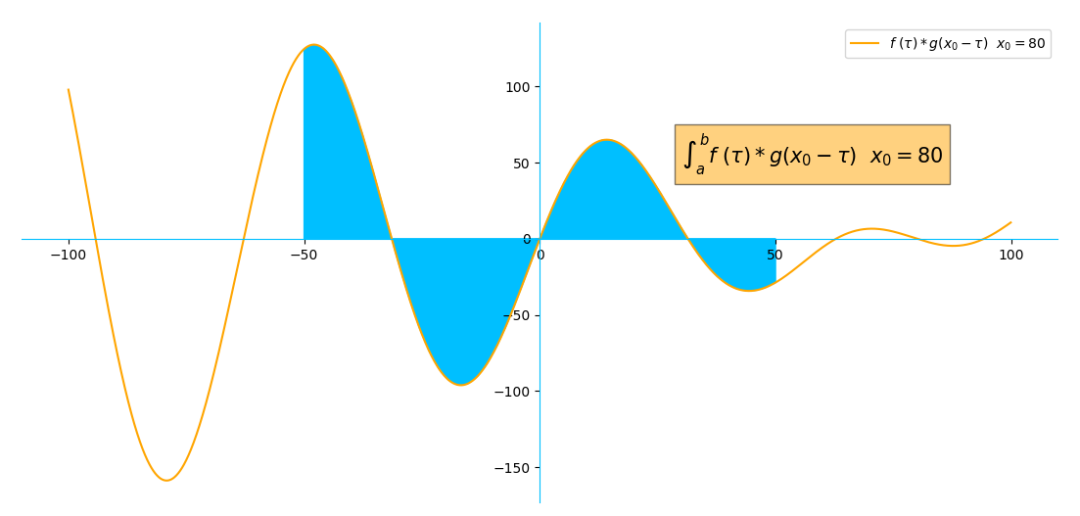
注意了,在上面的所有过程中,x 一直是不变的,变的是 τ 。即我们上面一直是在做的是公式2右边的计算,公式2如下:
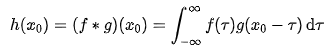
不论 τ怎么变化,最后一旦积分,等式右边就成了一个确定的数字,一个常量。一个 x 对应一个 y 嘛。此时我们可以继续看公式左边了,我们直接看公式1:
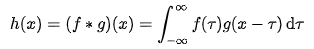
左边换下位置我们也许会更好理解,即 ( f * g )( x ) = h( x ) 。也即之前提到的一句话:卷积即是通过两个函数 f 和 g 生成第三个函数的一种数学算子。
总结一下,卷积计算过程可以分解为四步:翻转、平移、乘积、积分。
卷积为什么叫“卷积”?
1. 卷积之【卷】
那么问题来了?卷积为什么要叫“卷积”呢?换言之,卷积之“卷”和卷积之“积”分别是什么含义?
这里想像一下如果我们要卷起一张A4纸,需要怎么做?
(1)首先我们需要提起对着自己一条边,向上翻转使之对着自己身体前方——翻转!

(2)然后继续向下打个圈之后,就可以向前推了——平移!

看到没?翻转!平移!
你肯定还记得上面说的卷积计算的四个过程:翻转、平移、乘积、积分。卷积之“卷”,你明白了吗?
本文完
什么?还不能走?你想要画图的源码?
# coding:utf-8
"""
Author: CVPy-冰不语
Date: 2019/11/26
"""
import numpy as np
import matplotlib.pyplot as plt
# 定义函数f(x)
def f(x):
"""$f\ (\\tau)$"""
return x
# 定义函数g(x)
def g(x):
"""$f(x)=sin(x)$"""
return np.sin(x/10)
# 设置坐标系
def set_ax(ax):
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_color('deepskyblue')
ax.spines['left'].set_color('deepskyblue')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.set_xticks(np.arange(-100,101, 50))
# ax.set_yticks(np.arange(-100,101, 50))
return ax
if __name__ == "__main__":
# x的取值范围
x = np.arange(-100, 100, 0.1)
# ---------第一幅图:f(x)和f(-x)----------
fig = plt.figure(figsize=(6, 6))
# 左边画f(x)
ax1 = fig.add_subplot(121)
ax1 = set_ax(ax1)
ax1.plot(x, f(x), 'orange', label=f.__doc__)
plt.legend(loc="upper left", bbox_to_anchor=[0, 1],
ncol=1, fancybox=True)
# 右边画f(-x)
ax2 = fig.add_subplot(122)
ax2 = set_ax(ax2)
plt.plot(x, f(-x), 'orange', label="$f\ (-\\tau)$")
plt.legend(loc="upper right", bbox_to_anchor=[1, 1],
ncol=1, fancybox=True)
plt.show()
# ---------第二幅图:f(t-x)----------
fig2 = plt.figure(figsize=(6, 6))
ax3 = fig2.add_subplot(111)
ax3 = set_ax(ax3)
ax3.set_xticks(np.arange(-100, 101, 20))
ax3.set_yticks(np.arange(-100, 181, 20))
for t in [20, 40, 60, 80]:
plt.plot(x, f(t-x), label="$f\ (x_0 - \\tau) \ \ x_0={0}$".format(t))
plt.legend(loc="upper right", bbox_to_anchor=[1, 1], ncol=1, fancybox=True)
plt.show()
# ---------第三幅图:g(x) * f(t-x)----------
t = 80
def f_mul_g(x, t):
"""$f(\\tau-x)*g(\\tau)$"""
return f(t-x)*g(x)
fig3, ax4 = plt.subplots()
ax4 = set_ax(ax4)
ax4.set_xticks(np.arange(-100,101, 20))
# ax4.set_yticks(np.arange(-100,181, 20))
plt.plot(x, f_mul_g(x, t), label=f_mul_g.__doc__)
plt.legend(loc="upper right", bbox_to_anchor=[1, 1], ncol=1, fancybox=True)
plt.show()
# ---------第四幅图:g(x) * f(t-x)的积分----------
import matplotlib.patches as mPatches
def int_fg(x, t, ax5):
ax5 = set_ax(ax5)
plt.plot(x,f_mul_g(x, t), 'orange', label="$f\ (\\tau)*g(x_0-\\tau) \ \ x_0={0}$".format(t))
plt.legend(loc="upper right", bbox_to_anchor=[1, 1],
ncol=1, fancybox=True)
a = -50
b = 50
ix = np.linspace(a,b)
iy = f_mul_g(ix,t)
verts = [(a,0)] + list(zip(ix, iy)) + [(b,0)]
poly = mPatches.Polygon(verts,color='deepskyblue')
ax5.add_patch(poly)
# plt.plot(x,g(x),label=g.__doc__)
plt.text(30, 50, '$\int_a^b f\ (\\tau)*g(x_0-\\tau) \ \ x_0={0}$'.format(t), style='oblique',
bbox={'facecolor': 'orange', 'alpha': 0.5, 'pad': 5}, fontsize=15)
fig4, ax5 = plt.subplots()
int_fg(x, t, ax5)
plt.legend(loc="upper right", bbox_to_anchor=[1, 1], ncol=1, fancybox=True)
plt.ion()
# for i in range(100):
# y = np.random.random()
# plt.autoscale()
# plt.scatter(i, y)
# plt.pause(0.01)
fig4, ax5 = plt.subplots()
tn = np.arange(-100,100,5)
for t in tn:
plt.cla()
plt.grid(True)
plt.autoscale()
int_fg(x, t, ax5)
plt.pause(0.01)
plt.legend(loc="upper right", bbox_to_anchor=[1, 1], ncol=1, fancybox=True)
plt.show()本文转自: CVPy冰不语(微信号:x-cvpy),转载此文目的在于传递更多信息,版权归原作者所有。






