神经网络中损失函数后一般会加一个额外的正则项L1或L2,也称为L1范数和L2范数。正则项可以看做是损失函数的惩罚项,用来对损失函数中的系数做一些限制。
正则化描述:
L1正则化是指权值向量w中各个元素的绝对值之和;
L2正则化是指权值向量w中各个元素的平方和然后再求平方根;
一般都会在正则化项之前添加一个系数,这个系数需要用户设定,系数越大,正则化作用越明显。
正则化作用:
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择,一定程度上,L1也可以防止过拟合;
L2正则化可以防止模型过拟合(overfitting);
何为稀疏矩阵
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵。
神经网络中输入的特征数量是庞大的,如何选取有效的特征进行分类是神经网络的重要任务之一,如果神经网络是一个稀疏模型,表示只有少数有效的特征(系数非0)可以通过网络,绝大多数特征会被滤除(系数为0),这些被滤除的特征就是对模型没有贡献的“无关”特征,而少数系数是非0值的特征是我们需要额外关注的有效特征。也就是说,稀疏矩阵可以用于特征选择。
L1正则化是怎么做到产生稀疏模型的?
假设有如下带L1正则化的损失函数:
Loss = Loss_0 + αL1
Loss_0是原始损失函数,L1是加的正则化项,α 是正则化系数,其中 L1 是 模型中权重 w 的绝对值之和。
神经网络训练的目标就是通过随机梯度下降等方法找到损失函数 Loss的最小值,加了L1之后,相当于对原始Loss_0做了一个约束,即在 L1 约束下求Loss_0最小值的解。
对于最简单的情况,假设模型中只有两个权值 w1 和 w2 ,对于梯度下降法,可以分别画出求解 Loss_0 和 L1 过程中的等值线,如下图:
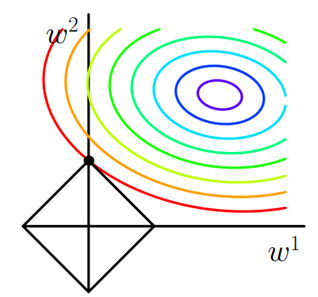
等值线是说在等值线上任一点处(取不同的w1和w2组合),模型计算的结果都是一样的。
图中彩色弧线是Loss_0的等值线,黑色方框是 L1的等值线。在图中,当Loss_0等值线与L1图形首次相交的地方就是一个最优解,这个相交的点刚好是L1的顶点。
注意到L1函数有很多个突出的点,二维情况下有4个,维数越多顶点越多,这些突出的点会比线段上的点有更大的几率首先接触到 Loss_0的等值线,而这些顶点正好对应有很多权值为0的矩阵, 即稀疏矩阵,这也就是为什么L1正则化可以用来产生稀疏矩阵进而用来进行特征选择的原因。
对于L1正则化前的系数α,是用来控制L1图形的大小,α越大,L1中各个系数就相对越小(因为优化目标之一是α×L1的值趋近于0。α大,L1系数取值就会小),L1的图形就越小; α越小,L1中各个系数就相对越大,L1的图形就越大。
L2正则化是怎么做到防止模型过拟合的?
仍以最简单的模型,只有两个权重w1 和 w2为例,Loss_0和L2分别对应的等值线形状如下图:

由于L2是w1和w2平方和再开方,所以L2的图形是一个圆。圆形相对方形来说没有顶点,Loss_0 和 L2图形相交使得 w1或者w2等于的概率大大减小,所以L2正则化项不适合产生稀疏矩阵,不适合用来选择特征。
相对来说,模型中所有矩阵系数都比较小的模型具有更强的抗干扰能力,也就是说可以避免过拟合。对于这种小系数的模型,特征会乘以很小的系数,使得特征的波动被压缩,所以泛化能力更好。
L2正则化项的公式是所有权重系数平方之后再开方,所以在每次迭代过程中, 都会使得权重系数在满足最小化Loss_0的基础上,一步一步使得权重系数w1和w2趋向于0,最终得到权重系数很小的矩阵模型,达到防止过拟合的作用。
对于L1正则化项,如果α系数取很大,也会得到系数极小的最优解,这时的L1也具有防止过拟合的作用。
L1和L2中的α系数的作用是类似的,α系数越大,正则化作用越明显(但同时也可能意味着模型越难以收敛),从等值图上直观看就是L图形越小,对应矩阵系数越小。
本文转自:博客园 - 未雨愁眸 ,转载此文目的在于传递更多信息,版权归原作者所有。