近日,Judea Pearl 发表技术报告,指出当前机器学习的三个主要障碍,并提出了人工智能范式的完整结构应该包含三个层级,而当前的机器学习尚处于底层,最后他列举了七个用于克服这些障碍的因果推理工具。
引言
机器学习的巨大成功带来了 AI 应用的爆炸式增长以及对具备人类级别智能的自动化系统不断增长的期望。然而,这些期望在很多应用领域中都遇到了基本的障碍。其中一个障碍就是适应性或鲁棒性。机器学习研究者注意到当前的系统缺乏识别或响应未经特定编程或训练的新环境的能力。人们在「迁移学习」、「域适应」和「终身学习」[Chen and Liu 2016] 这些方向进行大量理论和实验研究就是为了克服这个障碍。
另一个障碍是可解释性,即「机器学习模型仍然主要是黑箱的形式,无法解释其预测或推荐背后的原因,因此降低了用户的信任,阻碍了系统诊断和修复。」[Marcus 2018]
第三个障碍和对因果关系的理解相关。理解因果关系这一人类认知能力的标志是达到人类级别智能的必要(非充分)条件。这个要素应该使计算机系统对环境进行简洁的编码和模块化的表征,对表征进行质询,通过想象对表征进行变化,并最终回答类似「如果……会如何?」这样的问题。例如,干预性的问题:「如果我让……发生了会如何?」,以及回溯性或解释性的问题:「如果我采取不同的做法会如何?」或「如果某件事情没有发生会如何?」
Pearl 假设以上三个障碍需要用结合了因果建模工具的机器来解决,特别是因果图示和它们的相关逻辑。图模型和结构模型的进展使得反事实推理在计算上可行,因此使得因果推理成为强人工智能中的有效组件。
在下一部分中,作者将描述限制和支配因果推理的三个层级。最后一部分总结了如何使用因果推理的现代工具避免传统机器学习的障碍。
三层因果层级
因果模型揭示的一个有用观点是按照问题类型对因果信息进行分类,每个类别能够回答特定的问题。该分类形成了一个三层的层级结构,只有在获取第 j 层(j ≥ i)信息时,第 i 层(i = 1, 2, 3)的问题才能够被解答。
图 1 展示了该三层层级结构,以及每一层可回答的典型问题。这三层的名字分别是 1. 关联(Association)、2. 干预(Intervention)、3. 反事实(Counterfactual)。这些名字是为了凸显每一层的作用。作者将第一层叫做「关联」是因为它仅仅调用统计关系,由裸数据来定义。例如,观察一位购买牙膏的顾客使得他/她购买牙线的可能性增大;此类关联可以使用条件期望直接从观测数据中推断得到。这一层的问题不需要因果信息,因此它们可以被放置在该三层层级架构的最底层。第二层「干预」层次比「关联」高,因为它不只涉及观察,还会改变观察到的信息。这一层的典型问题是:如果我们把价格提高一倍会怎样?此类问题无法仅根据销售数据来回答,因为它们涉及顾客行为针对新价格所作出的改变。这些选择可能与之前的提价情况中顾客所作出的选择大相径庭。(除非我们精确复制价格提高一倍时的已有市场条件。)最后,顶层是「反事实」,「反事实」一词可以追溯到哲学家 David Hume 和 John Stewart Mill,在过去二十年中「反事实」被赋予了和计算机有关的语义。这一层的典型问题是「如果我采取不同的做法会怎样」,因此需要回溯推理(retrospective reasoning)。
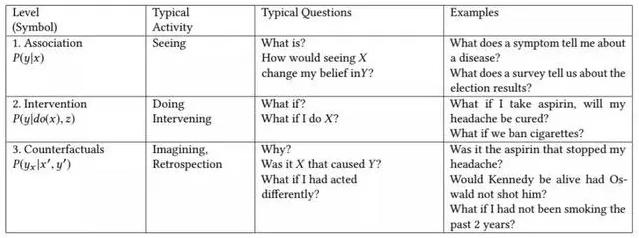
因果推理的 7 个工具(或只有使用因果模型才能做到的事情)
考虑以下 5 个问题:
* 给定的疗法在治疗某种疾病上的有效性?
* 是新的税收优惠导致了销量上升吗?
* 每年的医疗费用上升是由于肥胖症人数的增多吗?
* 招聘记录可以证明雇主的性别歧视罪吗?
* 我应该放弃我的工作吗?
这些问题的一般特征是它们关心的都是原因和效应的关系,可以通过诸如「治疗」、「导致」、「由于」、「证明」和「我应该」等词识别出这类关系。这些词在日常语言中很常见,并且我们的社会一直都需要这些问题的答案。然而,直到最近也没有足够好的科学方法对这些问题进行表达,更不用说回答这些问题了。和几何学、机械学、光学或概率论的规律不同,原因和效应的规律曾被认为不适合应用数学方法进行分析。
这种误解有多严重呢?实际上仅几十年前科学家还不能为明显的事实「mud does not cause rain」写下一个数学方程。即使是今天,也只有顶尖的科学社区能写出这样的方程并形式地区分「mud causes rain」和「rain causes mud」。
过去三十年事情已发生巨大变化。一种强大而透明的数学语言已被开发用于处理因果关系,伴随着一套把因果分析转化为数学博弈的工具。这些工具允许我们表达因果问题,用图和代数形式正式编纂我们现有的知识,然后利用我们的数据来估计答案。进而,这警告我们当现有知识或可获得的数据不足以回答我们的问题时,暗示额外的知识或数据源以使问题变的可回答。
作者把这种转化称为「因果革命」(Pearl and Mackenzie, 2018, forthcoming),而导致因果革命的数理框架称之为「结构性因果模型」(SCM)。
SCM 由三部分构成:
1. 图模型
2. 结构化方程
3. 反事实和介入式逻辑
图模型作为表征知识的语言,反事实逻辑帮助表达问题,结构化方程以清晰的语义将前两者关联起来。
图 2 描述了 SCM 作为推断引擎时的运行流程。该引擎接受三种输入:假设(Assumptions)、查询(Queries)和数据(Data),并生成三种输出:被估量(Estimand)、估计值(Estimate)和拟合指数(fit indices)。被估量(E_S)是一个数学公式,该公式基于假设,提供从任意假设数据中回答查询的方法(可获取假设数据的情况下)。在接收到数据后,该引擎使用被估量来生成问题的实际估计值 E_s hat,以及问题置信度的统计估计值(以反映数据集的有限规模,以及可能的衡量误差或缺失数据)。最后,该引擎生成一个「拟合指数」列表,可衡量数据与模型传递的假设的兼容性。
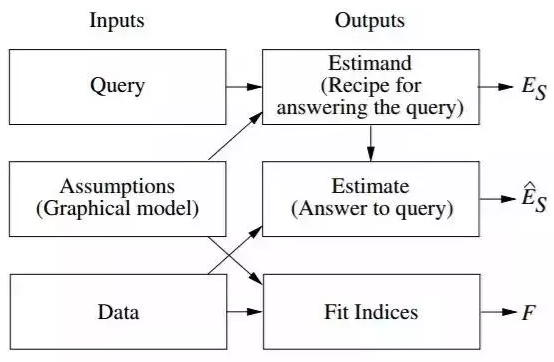
接下来介绍 SCM 框架的 7 项最重要的特性,并讨论每项特性对自动化推理做出的独特贡献。
1. 编码因果假设—透明性和可试性
图模型可以用紧凑的格式编码因果假设,同时保留透明性和可试性。其透明性使我们可以了解编码的假设是否可信(科学意义上),以及是否有必要添加其它假设。可试性使我们(作为人类或机器)决定编码的假设是否与可用的数据相容,如果不相容,分辨出需要修改的假设。利用 d-分离(d-separate)的图形标准有助于以上过程的执行,d-分离构成了原因和概率之间的关联。通过 d-分离可以知道,对模型中任意给定的路径模式,哪些依赖关系的模式才是数据中应该存在的(Pearl,1988)。
2. do-calculus 和混杂控制
混杂是从数据中提取因果推理的主要障碍,通过利用一种称为「back-door」的图形标准可以完全地「解混杂」。特别地,为混杂控制选择一个合适的协变量集合的任务已被简化为一种简单的「roadblocks」问题,并可用简单的算法求解。(Pearl,1993)
为了应对「back-door」标准不适用的情况,人们开发了一种符号引擎,称为 do-calculus,只要条件适宜,它可以预测策略干预的效应。每当预测不能由具体的假设确定的时候,会以失败退出(Pearl, 1995; Tian and Pearl, 2002; Shpitser and Pearl, 2008)。
3. 反事实算法
反事实分析处理的是特定个体的行为,以确定清晰的特征集合。例如,假定 Joe 的薪水为 Y=y,他上过 X=x 年的大学,那么 Joe 接受多一年教育的话,他的薪水将会是多少?
在图形表示中使用反事实推理是将因果推理应用于编码科学知识的非常有代表性的研究。每一个结构化方程都决定了每一个反事实语句的真值。因此,我们可以解析地确定关于语句真实性的概率是不是可以从实验或观察研究(或实验加观察)中进行估计(Balke and Pearl, 1994; Pearl, 2000, Chapter 7)。
人们在因果论述中特别感兴趣的是关注「效应的原因」的反事实问题(和「原因的效应」相对)。(Pearl,2015)
4. 调解分析和直接、间接效应的评估
调解分析关心的是将变化从原因传递到效应的机制。对中间机制的检测是生成解释的基础,且必须应用反事实逻辑帮助进行检测。反事实的图形表征使我们能定义直接和间接效应,并确定这些效应可从数据或实验中评估的条件(Robins and Greenland, 1992; Pearl, 2001; VanderWeele, 2015)
5. 外部效度和样本选择偏差
每项实验研究的有效性都需要考虑实验和现实设置的差异。不能期待在某个环境中训练的模型可以在环境改变的时候保持高性能,除非变化是局域的、可识别的。上面讨论的 do-calculus 提供了完整的方法论用于克服这种偏差来源。它可以用于重新调整学习策略、规避环境变化,以及控制由非代表性样本带来的偏差(Bareinboim and Pearl, 2016)。
6. 数据丢失
数据丢失的问题困扰着实验科学的所有领域。回答者不会在调查问卷上填写所有的条目,传感器无法捕捉环境中的所有变化,以及病人经常不知为何从临床研究中突然退出。对于这个问题,大量的文献致力于统计分析的黑箱模型范式。使用缺失过程的因果模型,我们可以形式化从不完整数据中恢复因果和概率的关系的条件,并且只要条件被满足,就可以生成对所需关系的一致性估计(Mohan and Pearl, 2017)。
7. 挖掘因果关系
上述的 d-分离标准使我们能检测和列举给定因果模型的可测试推断。这为利用不精确的假设、和数据相容的模型集合进行推理提供了可能,并可以对模型集合进行紧凑的表征。人们已在特定的情景中做过系统化的研究,可以显著地精简紧凑模型的集合,从而可以直接从该集合中评估因果问询。
技术报告:The Seven Tools of Causal Inference with Reflections on Machine Learning

报告地址:http://ftp.cs.ucla.edu/pub/stat_ser/r481.pdf
本文转自:机器人网






