啥是Gamma Correction?什么是在线性空间(Linear Space)中做光照计算?
线性空间这玩意已经说烂了,不过再烂也不是生而知之,该学还得学,这里总结一下。
先介绍下啥是Gamma(别急,先看下去,这是解释线性空间的前置知识)。这词儿N多人听说过,而且也被各种滥用。这里只解释游戏即时渲染相关的概念。首先,就是老式CRT显示器的一个问题,给显示器输入的电压和输出的亮度不成线性关系,啥意思呢,就是你告诉显示器我这个像素颜色是0.5,显示器给个亮度,然后你说下个像素颜色是1.0,然后显示器给的亮度不是上一个亮度的两倍,而是成下面这个函数的关系:
Y = pow(X, Gamma)
也就是输出是输入的Gamma次方。而一般来说这个Gamma值是2.2(具体值根据各种标准不太一样,这里统一认为是2.2)
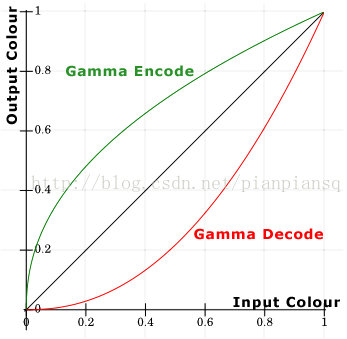
红色的曲线就是Y = pow(X, 2.2)的曲线,可以看出,显示器输出的图片是会比想象中的暗的。那么咋办呢,各种图片,视频等其实在进行数据储存的时候,都会做Gamma Encode(也会被称为Gamma Correction,这个词可能会被用到各种地方,包括Gamma Decode也会被称为Gamma Correction,为了防止混乱,这里就不这么叫了干脆)。举个例子,照相的时候,你相机照下照片后是会做一系列后处理,然后再存到SD卡里的,其中有一项后处理就是Gamma Encode,也就是将整体画面“调亮”,然后显示器再显示的时候,再做一次Gamma Decode,这样显示的画面就Gamma抵消了,亮度刚好OK。(你应该注意到高级相机都会可能储存raw这个格式的图片,超级大,这种图片是没有做Gamma Encode的,就是纯记录下来的原始数据。那么显示为啥还正确呢,是因为大部分能打开raw文件的软件,都知道你没做Gamma Encode,所以软件会在显示图片前给Encode一下)。虽然现代的LCD显示器已经没有自带的Gamma Decode“功能”了,但是为了兼容以前的显示器,还是会调一个Gamme Decode出来。
除此以外,各种图片视频会做Gamma Encode的原因还有一个,就是人眼识别光线亮暗的敏感度是不一样的,人眼在看暗处的时候会比看亮的更加敏感。而由于图片一般使用8bit每color channel,也就是所谓的24位真彩色,这个储存数据如果平均分配亮暗程度的话,那么给暗处的数据量会不够,人眼会看出明显“色带”问题,而如果做了Gamma Encode的话,刚刚好(这可真是凑巧)是把暗处信息储存更多,而且存储的比例也刚好差不多符合人眼对于亮暗敏感程度的比例,这种存储的图像空间就是耳熟能详的sRGB图像空间。
下图就是如果用Linear Encode的话,显示是什么样子的,为了更加显眼,用的是32阶的5bit储存。注意看暗部细节,明显不够用,而Gamma Encode则是亮暗部很均衡。

Linear Encode in 5 bits

Gamma Encode in 5 bits
说了半天都是在讲Gamma相关的东西,现在终于说到和游戏相关的了,其实可能已经猜到了,传统渲染流程中根本就没有处理Gamma这个东西,是下面这个流程:

这个流程是错的,因为直接使用了Encoded Gamma图去做光照计算,也就是说,使用了非线性的输入来进行线性计算(shader中计算光照可都是线性的),出来的结果自然是错误的。正确做法是先把图片转到线性空间(Gamma Decode),然后进行光照计算,然后再把计算结果做Gamma Encode,再输出给屏幕,也就是下面这个流程图:
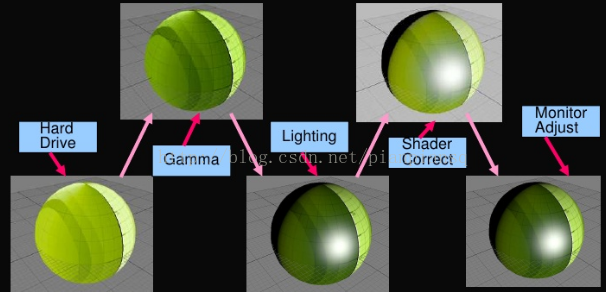
现在对比下两者的区别,上面的是错误的,下面是正确的。可以看出,由于计算错误,高光部分已经奇怪的从白色偏移到黄绿色了。我知道很多人觉得上面那个阴影过度很好看,但是如果你观察现实的话,你会发现现实中的过度边界就是下面那么“硬”,如下图:

如果你喜欢错误的那种阴影过度样式,也应该去调整shader专门做相关渲染,而不是用一个错误结果的副产品将就了。
而哪些贴图需要提前做Gamma Decode呢,原则上来说是Diffuse贴图。而Normal, Metal, Roughness等只是拿贴图储存数据,而不是颜色的贴图则不要做Gamma Decode。
参考:
1. http://www.cambridgeincolour.com/tutorials/gamma-correction.htm
2. http://www.codinglabs.net/article_gamma_vs_linear.aspx
3. http://www.slideshare.net/ozlael/hable-john-uncharted2-hdr-lighting
版权声明:本文为CSDN博主「pianpiansq」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/pianpiansq/article/details/54645738






