现实中常遇到多分类学习任务。有些二分类学习方法可直接推广到多分类,如LR。但在更多情形下,我们是基于一些基本策略,利用二分类学习器来解决多分类问题。所以多分类问题的根本方法依然是二分类问题。
具体来说,有以下三种策略:
一、一对一 (OvO)
假如某个分类中有N个类别,我们将这N个类别进行两两配对(两两配对后转化为二分类问题)。那么我们可以得到 个二分类器。(简单解释一下,相当于在N个类别里面抽2个)
个二分类器。(简单解释一下,相当于在N个类别里面抽2个)
之后,在测试阶段,我们把新样本交给这 个二分类器。于是我们可以得到
个二分类器。于是我们可以得到 个分类结果。把预测的最多的类别作为预测的结果。
个分类结果。把预测的最多的类别作为预测的结果。
下面,我给一个具体的例子来理解一下。

上图的意思其实很明显,首先把类别两两组合(6种组合)。组合完之后,其中一个类别作为正类,另一个作为负类(这个正负只是相对而言,目的是转化为二分类)。然后对每个二分类器进行训练。可以得到6个二分类器。然后把测试样本在6个二分类器上面进行预测。从结果上可以看到,类别1被预测的最多,故测试样本属于类别1。
二、一对其余 (OvR)
一对其余其实更加好理解,每次将一个类别作为正类,其余类别作为负类。此时共有(N个分类器)。在测试的时候若仅有一个分类器预测为正类,则对应的类别标记为最终的分类结果。例如下面这个例子。
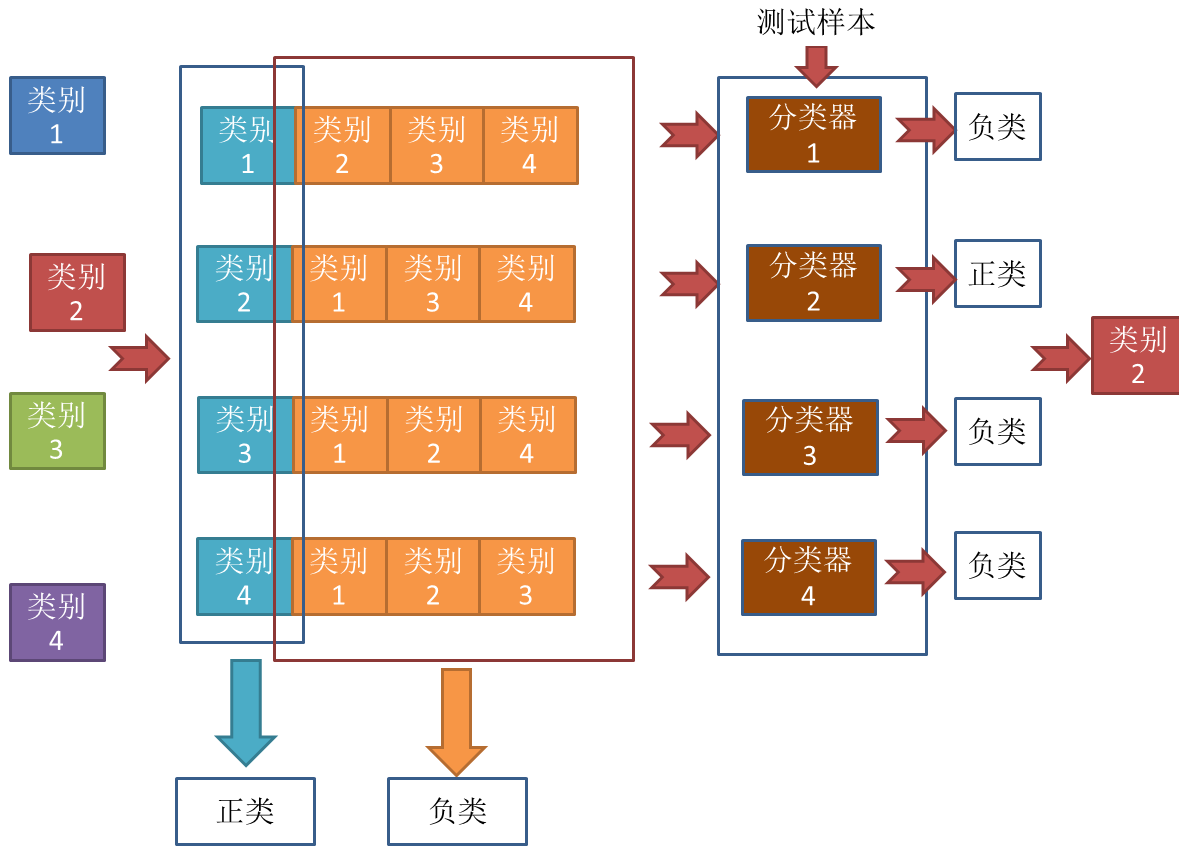
大概解释一下,就是有当有4个类别的时候,每次把其中一个类别作为正类别,其余作为负类别,共有4种组合,对于这4中组合进行分类器的训练,我们可以得到4个分类器。对于测试样本,放进4个分类器进行预测,仅有一个分类器预测为正类,于是取这个分类器的结果作为预测结果,分类器2预测的结果是类别2,于是这个样本便属于类别2。
其实,有人会有疑问,那么预测为负类的分类器就不用管了吗?是的,因为预测为负类的时候有多种可能,无法确定,只有预测为正类的时候才能唯一确定属于哪一类。比如对于分类器3,分类结果是负类,但是负类有类别1,类别2,类别4三种,到底属于哪一种?
OvO和OvR有何优缺点?
容易看出,OvR只需训练N个分类器,而OvO需训练N(N - 1)/2个分类器, 因此,OvO的存储开销和测试时间开销通常比OvR更大。但在训练时,OvR的每个分类器均使用全部训练样例,而OvO的每个分类器仅用到两个类的样例,因此,在类别很多时,OvO的训练时间开销通常比OvR更小。至于预测性能,则取决于具体的数据分布,在多数情形下两者差不多。
综上:
OvO的优点是,在类别很多时,训练时间要比OvR少。缺点是,分类器个数多。
OvR的优点是,分类器个数少,存储开销和测试时间比OvO少。缺点是,类别很多时,训练时间长。
三、多对多(MvM)
MvM是每次将若干个类作为正类,若干个其他类作为反类。显然,OvO和OvR是MvM的特例。MvM的正、反类构造必须有特殊的设计,不能随意选取。这里我们介绍一种最常用的MvM技术"纠错输出码" (Error Correcting Output Codes,简称 ECOC)
ECOC是将编码的思想引入类别拆分,并尽可能在解码过程中具有容错性。ECOC工作过程主要分为两步:
----编码:对N个类别做M次划分,每次划分将一部分类别划为正类,一部分划为反类,从而形成一个二分类训练集。这样一共产生M个训练集,可训练出M个分类器。
----解码:M 个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
类别划分通过"编码矩阵"指定。编码矩阵有多种形式,常见的主要有二元码和三元码。前者将每个类别分别指定为正类和反类,后者在正、反类之外,还可指定"停用类"。图3.5给出了一个示意图,在图 3.5(a) 中,分类器f2将Cl类和C3类的样例作为正例,C2类和C4类的样例作为反例;在图3.5(b)中,分类器f4将C1类和C4类的样例作为正例,C3 类的样例作为反例。在解码阶段,各分类器的预测结果联合起来形成了测试示例的编码,该编码与各类所对应的编码进行比较,将距离最小的编码所对应的类别作为预测结果。
例如在图 3.5(a) 中,若基于欧式距离,预测结果将是 C3。也就是一个测试样本,经过分类器f1,f2,f3,f4,f5分别预测成了(-1,-1,+1,-1,+1),与C1相比较,海明距离为0+1+1+1+0=3,欧式距离为,对C2,C3,C4都进行比较即可。

为什么称为"纠错输出码"呢?
这是因为在测试阶段,ECOC编码对分类器的错误有一定的容忍和修正能力。例如图3.5(a) 中对测试示例的正确预测编码是(-1,+1,+1,-1,+1),假设在预测时某个分类器出错了,例如 h 出错从而导致了错误编码(-1,-1,+1,-1,+1),但基于这个编码仍能产生正确的最终分类结果C3。一般来说,对同一个学习任务,ECOC编码越长,纠错能力越强。
EOCO编码长度越长,纠错能力越强,那长度越长越好吗?
NO!编码越长,意味着所需训练的分类器越多,计算、存储开销都会增大;另一方面,对有限类别数,可能的组合数目是有限的,码长超过一定范围后就失去了意义。
对同等长度的编码,理论上来说,任意两个类别之间的编码距离越远,则纠错能力越强。因此,在码长较小时可根据这个原则计算出理论最优编码。然而,码长稍大一些就难以有效地确定最优编码,事实上这是 NP 难问题。不过,通常我们并不需获得理论最优编码,因为非最优编码在实践中往往己能产生足够好的分类器。另一方面,并不是编码的理论性质越好,分类性能就越好,因为机器学习问题涉及很多因素,例如将多个类拆解为两个“类别子集”,不同拆解方式所形成的两个类别子集的区分难度往往不同,即其导致的二分类问题的难度不同。于是一个理论纠错牲质很好、但导致的二分类问题较难的编码,与另一个理论纠错性质差一些、但导致的二分类问题较简单的编码,最终产生的模型性能孰强孰弱很难说。
参考文献:
https://blog.csdn.net/u012679707/article/details/80527994
https://blog.csdn.net/anshuai_aw1/article/details/82902853
版权声明:本文为CSDN博主「anshuai_aw1」的原创文章,遵循CC 4.0 by-sa版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/anshuai_aw1/article/details/82973039






