图像配准方法主要分为三类:一种是灰度方法信息方法,另一种是基于特征的方法,可细分为特征点、直线段、边缘轮廓、特征结构以及矩不变统计特征等,还有一种就是基于变换域的方法,如相位相关、Walsh Transform等方法。傅里叶-梅林变换就是一种变换域的方法。
在图像配准过程中,常常需要处理平移、旋转、尺度变换、遮挡、形变等问题,使用傅里叶-梅林变换可以很好的应对平移、平面内旋转、缩放和遮挡,是一种鲁棒性较强的方法。这篇博客讲详细介绍傅里叶-梅林变换的性质,以及其在图像配准过程中的应用。
一、原理
将笛卡尔坐标系下的旋转和缩放转化为新坐标系下的平移,通过相位相关求得平移量就得到了缩放倍率和旋转角度。根据倍率和旋转角度做矫正,再直接相位相关求得平移量。于是就得到了两幅图像的相对位移、旋转和缩放,可以用于图像配准。
二、步骤
1. 产生两个等大的正方形图像块
2. 对这两个图像块分别做傅里叶变换、对数极坐标变换(统称傅里叶梅林变换),右图就是变换结果
3. 再做傅里叶变换,然后相位相关,再逆变换就得到了响应图
4. 寻找响应图最大值位置,然后查表得到旋转角度和缩放倍率
以上部分求得旋转、缩放,还有平移没有求
以下部分没有写代码
5. 同样适用相位相关求平移
下图是计算出的响应图像
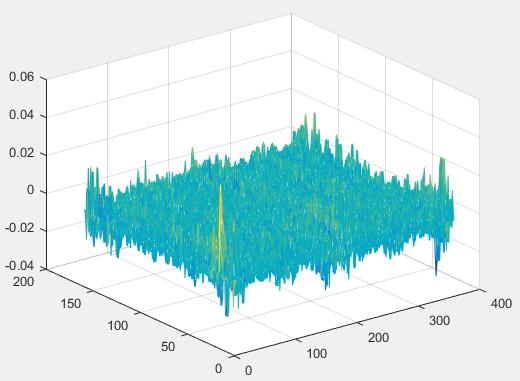
三、代码
本文转自:DEEP STUDIO,转载此文目的在于传递更多信息,版权归原作者所有。






