在进行图像处理的过程中,获取原始图像后,首先需要对图像进行预处理,因为在获取图像的过程中,往往会发生图像失真,使所得图像与原图像有某种程度上的差别。在许多情况下,人们难以确切了解引起图像降质的具体物理过程及其数学模型,但却能估计出使图像降质的一些可能原因,针对这些原因采取简单易行的方法,改善图像质量。
图像增强一般不能增加原图像信息,只能针对一些成像条件,把弱信号突出出来,使一些信息更容易分辨。
图像增强的方法分为频域法和空域法,空域法主要是对图像中的各像素点进行操作;而频域法是在图像的某个变换域内,修改变换后的系数,例如傅立叶变换、DCT 变换等的系数,对图像进行操作,然后再进行反变换得到处理后的图像。
下面具体对频域增强的方法进行介绍。
频域增强定义和步骤
频域增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其它空间中,然后利用该空间的特有性质方便地进行图像处理,最后再转换回原来的图像空间中,从而得到处理后的图像。
频域增强的主要步骤是:
(1) 选择变换方法,将输入图像变换到频域空间;
(2) 在频域空间中,根据处理目的设计一个转移函数并进行处理;
(3) 将所得结果用反变换得到图像增强。
低通滤波
图像在传递过程中,由于噪声主要集中在高频部分,为去除噪声改善图像质量,滤波器采用低通滤波器H(u,v)来抑制高频成分,通过低频成分,然后再进行逆傅立叶变换获
得滤波图像,就可达到平滑图像的目的。在傅里叶变换域中,变换系数能反映某些图像的特征,如频谱的直流分量对应于图像的平均亮度,噪声对应于频率较高的区域,图像实体位于频率较低的区域等,因此频域常被用于图像增强。在图像增强中构造低通滤波器,使低频分量能够顺利通过,高频分量有效地阻止,即可滤除该领域内噪声。由卷积定理,低通滤波器数学表达式[3]为:G(u,v) = F(u,v)H(u,v) (1)式中,F(u,v)为含有噪声的原图像的傅里叶变换域;H(u,v)为传递函数;G(u,v)为经低通滤波后输出图像的傅里叶变换。假定噪声和信号成分在频率上可分离,且噪声表现为高频成分。H 滤波滤去了高频成分,而低频信息基本无损失地通过。
选择合适的传递函数H(u,v)对频域低通滤波关系重大。常用频率域低滤波器H(u,v)有四种:
(1) 理想低通滤波器
设傅立叶平面上理想低通滤波器离开原点的截止频率
为D0,则理想低通滤波器的传递函数为:
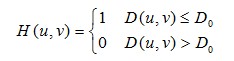
式中,D ( u , v ) = ( u2 + v2 )1/2 表示点(u,v)到原点的距离,D0 表示截止频率点到原点的距离。
下图中在频域坐标系(u , v ) 中,D(u , v ) 表示点(u , v ) 到原点的距离,图中红色圆周上的点距离原点的距离为D0,进行理想低通过滤的话,在圆周外面的将全部变暗(没有能量)。

(2) Butterworth 低通滤波器
n 阶Butterworth 滤波器的传递函数为:

(3) 指数滤波器
指数高通滤波器的传递函数为:
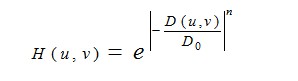
(4) 梯形低通滤波器
梯形高通滤波器的定义为:
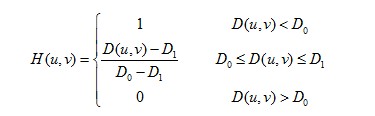
高通滤波
图像中的细节部分与其频率的高频分量相对应,所以高通滤波可以对图像进行锐化处理。高通滤波器与低通滤波器的作用相反,它使高频分量顺利通过,而消弱低频。
图像的边缘、细节主要位于高频部分,而图像的模糊是由于高频成分比较弱产生的。采用高通滤波器可以对图像进行锐化处理,是为了消除模糊,突出边缘。因此采用高通滤波器让高频成分通过,使低频成分削弱,再经逆傅立叶变换得到边缘锐化的图像。常用的高通滤波器有:
(1) 理想高通滤波器
二维理想高通滤波器的传递函数为:

(2) 巴特沃斯高通滤波器
n 阶巴特沃斯高通滤波器的传递函数定义如下:
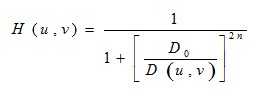
(3) 指数滤波器
指数高通滤波器的传递函数为:

(4) 梯形滤波器
梯形滤波器 的传递函数为:
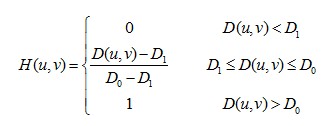
带通和带阻
带通滤波器容许一定频率范围信号通过, 但减弱(或减少)频率低于於下限截止频率和高于上限截止频率的信号的通过。带阻滤波器减弱(或减少)一定频率范围信号, 但容许频率低于於下限截止频率和高于上限截止频率的信号的通过。
同态滤波
一般来说,图像的边缘和噪声都对应于傅立叶变换的高频分量。而低频分量主要决定图像在平滑区域中总体灰度级的显示,故被低通滤波的图像比原图像少一些尖锐的细节部分。同样,被高通滤波的图像在图像的平滑区域中将减少一些灰度级的变化并突出细节部分。为了增强图像细节的同时尽量保留图像的低频分量,使用同态滤波方法 可以保留图像原貌的同时,对图像细节增强.
下面呈上指数和巴式的滤波程序
Java代码
本文转自:ITeye博客 - DSQiu,转载此文目的在于传递更多信息,版权归原作者所有。






