一、图简介，图卷积网络的出现。
图（graph）是一种数据格式，它可以用于表示社交网络、通信网络、蛋白分子网络等，图中的节点表示网络中的个体，连边表示个体之间的连接关系。许多机器学习任务例如社团发现、链路预测等都需要用到图结构数据，因此图卷积神经网络的出现为这些问题的解决提供了新的思路。
下图就是一个简单的图结构数据：
图上的神经网络，最早由Joan Bruna于2014年在论文Spectral Networks and Locally Connected Networks on Graph中提出。图卷积网络（简称GCN），由Thomas Kpif于2017年在论文Semi-supervised classification with graph convolutional networks中提出。它为图（graph）结构数据的处理提供了一个崭新的思路，将深度学习中常用于图像的卷积神经网络应用到图数据上。这个作者的博客中详细介绍了GCNGRAPH CONVOLUTIONAL NETWORKS
二、图卷积网络的卷积方式
图上的卷积网络从卷积方式上可以分为两种：
1. 谱（spectral）卷积，
2. 空间域卷积。
Thomas Kpif的这篇论文就是属于谱卷积，即将卷积网络的滤波器与图信号同时搬移到傅里叶域以后进行处理。而Mathias Niepert的论文Learning Convolutional Neural Networks for Graphs中的图卷积网络就属于空间域的卷积，即让图中的节点在空间域中相连、达成层级结构，进而进行卷积。其简单介绍可参见雷锋网文章 卷积神经网络不能处理“图”结构数据？这篇文章告诉你答案
三、图卷积网络的理论推导
下面介绍 Thomas Kpif 的论文 Semi-supervised classification with graph convolutional networks 中 GCN 的理论推导。
谱图卷积
将图的谱巻积定义为信号 x ∈ RN 与滤波器 gθ ＝ diag（θ）相乘，滤波器被傅里叶域的 θ∈RN 参数化：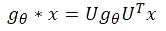
，U 是归一化图拉普拉斯矩阵的特征向量组成的矩阵，图拉普拉斯（矩阵）
Λ 是 L 的特征值组成的对角矩阵，UTx 是 x 的图傅里叶变换。我们可以将 gθ 理解为 L 的特征值的函数，即 gθ（Λ）。
在大图中计算 L 的特征值分解的复杂度很高，为了解决这个问题，用切比雪夫多项式 Tk（x）直到第 k
阶的截断展开来近似 gθ（Λ）
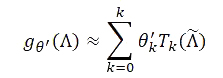
其中
，λmax 是 L 的最大特征值，θ'∈Rk 是切比雪夫系数向量。
切比雪夫多项式被定义为 Tk（x）＝ 2xTk－1（x）－Tk－2（x），其中T0（x）＝1，T1（x）＝ x 。
因此有如下表达式（5）
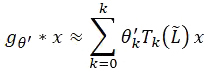
其中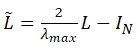
。此方程的复杂度为 
。
四、附言
近些年关于非欧几里德域的数据（图就属于非欧数据）如何处理的文章一大堆，现如今有几个概念很火：图嵌入（graph embedding）、网络嵌入（network embedding）、网络表示学习（network representation learning），这三个概念从原理上来说其实表达的是同一件事，核心思想就是“通过深度学习技术将图中的节点（或边）映射为向量空间中的点，进而可以对向量空间中的点进行聚类、分类等处理”。图卷积神经网络就属于图嵌入技术的一种，感兴趣的可以对图嵌入领域进行深入了解，你会发现宝藏不断：NE（Network Embedding）论文小览
本文为原创内容，欢迎转载、分享，请务必注明出处。
来源：CSDN ，作者：chensi1995
原文：https://blog.csdn.net/chensi1995/article/details/77232019
