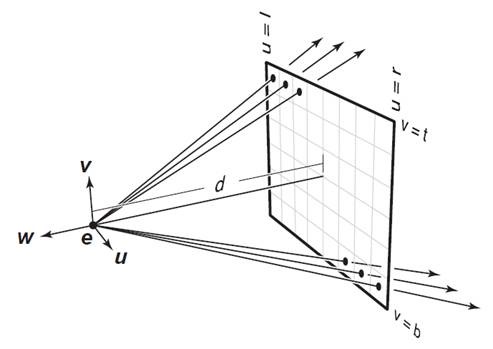
图形学离线渲染中常用的透视摄像机模型时根据小孔成像的原理建立的,其实现通常是从eye 向成像平面上发射ray,并把trace这条ray的结果作为成像平面上对应交点的采样结果。即:
现实中的镜头拍摄的图像有景深(Depth of field)的效果,譬如:

显然,上图中的耳机被放在摄像机的焦平面附近,成像很清晰;背景中的景物则离焦平面较远,呈现出模糊的效果。对离线渲染而言,这一效果有利于加强渲染结果的真实性和层次感。但之前提到的摄像机模型过于简单,要得到景深,需要更精确的摄像机模型。
上图是网络上给出的关于景深的一张示意图,看起来复杂骇人。但稍微分析就能知道,使得不在焦平面上的景物显得模糊的最根本原因恰恰是焦平面的概念本身,如下图——
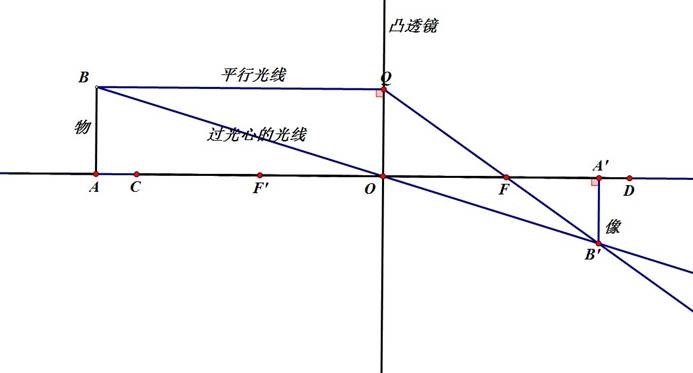
可以看到,假如在原来的透视摄像机模型中加入一个凸透镜,那么成像过程将不再是“一根”光线穿过小孔到达成像平面上的一点,而是许多光线透过凸透镜汇聚到成像平面上的一点。
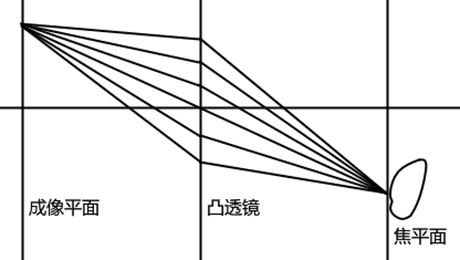
显然,假如有一物体正好在焦平面上,那么从上面某一点发射的光线通过凸透镜在成像平面上也会汇聚于一点,于是就得到了清晰的图像。但是,当物体不在焦平面上时,汇聚到成像平面上某一点的光线将不再全部来自于物体上的一点,而是来自于物体上的一小片区域,这就形成了模糊的效果,也就是最终看到的景深。
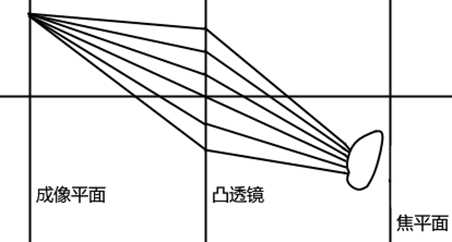
有了这一模型,要设计渲染出景深效果的算法就很容易了。以往从透视摄像机发射ray的方法是:
对成像平面上的一点P,发射射线P + t(p - e),其中 t >=0,e是eye点位置。
新的方法则是:
对成像平面上的一点P,求出射线P + t(o - p)与焦平面的交点 x,然后在凸透镜上随机采样(把凸透镜看做有一定半径的圆盘)。对每一个采样点 p',发射射线p' + t(x - p')。
新方法实质是在凸透镜所在的disk上对到达成像平面上特定点的能量用蒙特卡洛的方法进行了估值。
转自:AirGuanZ






