在计算机的数字世界中,数字的表示方式多种多样,而对于带有小数的数值计算,浮点运算发挥着关键作用。其中,FP32 和 FP16 作为两种重要的浮点数表示精度,在不同的计算场景中扮演着截然不同的角色。理解它们的特性、差异以及适用场景,对于充分发挥计算机算力,尤其是在当下热门的深度学习、科学计算等领域意义重大。
FP32:高精度的基石
FP32,即 32 位浮点数表示法,也被称为单精度浮点数。它在计算机中通过 32 个位来存储一个浮点数,具体组成如下:1 位用于表示数值的符号(正或负),8 位用于表示指数部分,这决定了数值的数量级大小,23 位用于表示尾数位,它体现了数值的精度细节 。例如,对于十进制数 9.625,转换为二进制是 1001.101,进一步转换为二进制指数形式为 1.001101×2³ 。在 FP32 表示中,指数部分需要加上 127 的偏移量,这里 3 + 127 = 130,对应的二进制表示为 10000010,小数部分补齐至 23 位后,结合符号位(这里为 0),最终得到完整的 FP32 表示。这种表示方式使得 FP32 能够表示的数值范围大约为 10^-38 到 10^38,具有约 7 - 9 位有效十进制数字的精度。
由于其较高的精度,FP32 在科学计算和工程模拟等领域堪称中流砥柱。在天体物理模拟中,计算星系的演化、星球的轨道等,任何微小的数值误差都可能随着时间的推演而被极度放大,从而导致模拟结果与实际情况谬以千里。在建筑工程的结构力学分析中,精确计算建筑在各种荷载下的应力应变,关乎建筑的安全与稳定,此时 FP32 的高精度确保了计算结果的可靠性与准确性。在深度学习早期,FP32 也是默认用于表示神经网络中大多数参数(如权重、偏差和激活值)的格式,因为它能较好地处理数值稳定性问题,减少梯度消失或爆炸等风险,有助于模型训练的稳定进行。
几乎所有现代计算硬件,无论是 CPU 还是 GPU,都原生支持 FP32 计算,在常见编程语言如 C、C++ 中,float 类型就对应着 FP32,在深度学习框架 TensorFlow 和 PyTorch 中,也分别通过 tf.float32 和 torch.float32 来便捷使用,这使得 FP32 在兼容性和普及性上具有无可比拟的优势。在科学计算和工程模拟领域,FP32 占据主导地位。像计算流体力学模拟飞行器周围的气流情况,精确的压力、流速等数值对于飞行器的设计优化至关重要,任何精度损失都可能导致飞行器性能预测不准确,影响飞行安全。量子力学计算中,对微观粒子的状态和相互作用的模拟,需要极高的精度来揭示物理规律,FP32 的高精度特性完全契合这类场景的需求 。而 FP16 由于其精度限制,在这类场景中应用较少,除非经过特殊处理和验证,确认其精度损失不会对结果产生实质性影响,否则很难在这些领域得到广泛应用。
FP16:高效计算的新宠
与 FP32 相对应的 FP16,是 16 位浮点数表示法,即半精度浮点数。它同样由符号位、指数位和尾数位组成,不过各部分所占位数与 FP32 有所不同:1 位符号位,5 位指数位和 10 位尾数位 。这种位数的减少,使得 FP16 在内存占用和计算速度方面展现出独特的优势。
在内存占用上,相比于 FP32,FP16 每个参数的内存占用直接减半。在大规模深度学习模型中,模型参数数量动辄数以亿计甚至更多,此时内存资源往往成为限制模型规模进一步扩大和训练效率提升的瓶颈。以 GPT-3 模型为例,其拥有数千亿个参数,若使用 FP32 存储这些参数,对内存的需求将极为庞大,而采用 FP16 后,内存占用大幅降低,使得在有限的硬件内存条件下,能够训练更大规模的模型,或者可以在相同内存下增加每次训练的样本数量(即 batch_size),进而提升训练效率。在计算速度方面,在支持 FP16 计算的现代 GPU(如 NVIDIA 的 V100、A100 等)上,由于数据宽度减半,一次能够处理更多的数据,其计算吞吐量显著提高,计算速度通常能达到 FP32 的两倍左右 。并且,数据量的减少使得在执行计算时能耗更低,能效比更高。
但 FP16 的这些优势并非毫无代价。由于指数位和尾数位的缩短,其表示的数值范围相对较窄,精度也低于 FP32。在某些对精度要求极为苛刻的复杂计算中,可能会因精度不足导致计算结果偏差较大,甚至在训练深度学习模型时,如果处理不当,可能出现数值不稳定,如梯度下溢或溢出等问题,进而影响模型的收敛性和最终性能 。不过,在实际应用中,尤其是深度学习领域,研究发现对于许多任务,在合理的技术处理下,FP16 的精度损失在可接受范围内,并且其带来的内存和计算优势远远超过了精度损失的影响。在深度学习训练阶段,FP32 一直以来是常用的精度格式,因其能够提供较高的数值精度,确保模型在训练过程中可以捕捉到数据中的细微特征和变化,有助于提升模型的准确性和泛化能力 。但随着模型规模的不断增大和对训练效率要求的日益提高,FP16 的优势逐渐凸显。许多深度学习框架开始支持 FP16 计算,并且通过一些技术手段,如混合精度训练技术,来平衡精度和效率。在推理阶段,尤其是在对实时性要求较高的场景,如自动驾驶汽车中的目标检测、人脸识别门禁系统等,FP16 因其计算速度快、内存占用小的特点,能够快速对输入数据进行处理并给出结果,得到了越来越广泛的应用 。例如,在一些边缘计算设备上,由于资源有限,使用 FP16 可以在不降低过多性能的前提下,大大提高推理速度,满足实时性需求。
二者在不同领域的应用对比
科学计算与工程模拟
在科学计算和工程模拟领域,FP32 占据主导地位。像计算流体力学模拟飞行器周围的气流情况,精确的压力、流速等数值对于飞行器的设计优化至关重要,任何精度损失都可能导致飞行器性能预测不准确,影响飞行安全。量子力学计算中,对微观粒子的状态和相互作用的模拟,需要极高的精度来揭示物理规律,FP32 的高精度特性完全契合这类场景的需求 。而 FP16 由于其精度限制,在这类场景中应用较少,除非经过特殊处理和验证,确认其精度损失不会对结果产生实质性影响,否则很难在这些领域得到广泛应用。
深度学习训练与推理
在深度学习训练阶段,FP32 一直以来是常用的精度格式,因其能够提供较高的数值精度,确保模型在训练过程中可以捕捉到数据中的细微特征和变化,有助于提升模型的准确性和泛化能力 。但随着模型规模的不断增大和对训练效率要求的日益提高,FP16 的优势逐渐凸显。许多深度学习框架开始支持 FP16 计算,并且通过一些技术手段,如混合精度训练技术,来平衡精度和效率。在推理阶段,尤其是在对实时性要求较高的场景,如自动驾驶汽车中的目标检测、人脸识别门禁系统等,FP16 因其计算速度快、内存占用小的特点,能够快速对输入数据进行处理并给出结果,得到了越来越广泛的应用 。例如,在一些边缘计算设备上,由于资源有限,使用 FP16 可以在不降低过多性能的前提下,大大提高推理速度,满足实时性需求。
混合精度训练:融合二者优势
为了充分利用 FP32 和 FP16 的优点,混合精度训练技术应运而生。其核心思路是在模型训练过程中,根据不同阶段和不同计算操作的特点,灵活选择使用 FP32 和 FP16。
在模型的前向传播过程中,由于这一阶段主要是数据的正向流动和计算,对精度要求相对没有那么苛刻,此时使用 FP16 进行计算,可以充分利用其计算速度快和内存占用小的优势,减少内存占用并加速计算过程 。而在反向传播过程中,由于需要计算梯度并更新模型参数,梯度的准确性对于模型的收敛和性能至关重要,因此通常会使用 FP32 来保证梯度计算的精度。另外,在一些关键的操作,如优化器的状态更新等,也使用 FP32 以确保模型训练的稳定性和收敛性 。为了应对在使用 FP16 进行计算时可能出现的数值过小导致精度损失的问题,还会采用 “损失缩放” 技术。具体做法是,在反向传播之前,将损失值扩大一定倍数,使得其在 FP16 可表示的范围内,进行反向计算得到梯度后,再将梯度缩小相同的倍数,以确保最终数值的准确性 。
以 NVIDIA 的 Ampere 架构 GPU 为例,其 Tensor Core 技术专门为加速混合精度计算而设计。在实际应用中,使用混合精度训练的模型在各项性能指标上与使用纯 FP32 训练的模型相当,但训练速度却有显著提升,同时内存使用效率也得到了提高。这使得混合精度训练成为一种在深度学习领域极具实用价值的技术,能够在不牺牲过多模型精度的前提下,有效提升训练效率和资源利用率 。
总结与展望
FP32 和 FP16 作为两种重要的算力精度格式,各有优劣,在不同的计算领域和应用场景中发挥着不可替代的作用。FP32 凭借其高精度,在对结果准确性要求极高的科学计算和工程模拟等领域稳固立足;FP16 则依靠内存占用小和计算速度快的优势,在深度学习等对计算效率和内存资源敏感的领域崭露头角 。混合精度训练技术更是巧妙地将二者结合,为深度学习模型的训练提供了更优的解决方案。
随着硬件技术的不断发展,未来我们有望看到对不同精度格式支持更加完善和高效的计算芯片,进一步提升计算性能和能效比。同时,软件算法和框架也将持续优化,更好地利用不同精度格式的特性,推动各个领域的计算任务朝着更高效、更智能的方向发展。无论是追求极致精度的科学研究,还是对效率要求严苛的工业应用和新兴的人工智能领域,FP32 和 FP16 以及它们衍生出的技术都将继续扮演重要角色,助力计算机技术不断突破创新。
为了帮助读者更好地理解 FP32 和 FP16 的差异,以下通过表格形式进行直观对比:
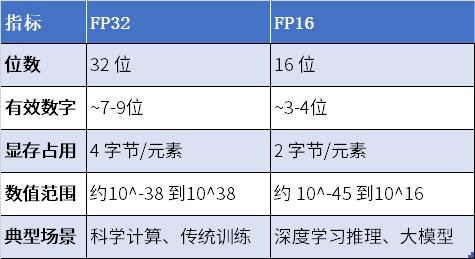
从表中可以清晰看出,在显存占用和数值范围方面,FP16 具有明显优势,适合对内存资源敏感的场景;而 FP32 凭借更多的有效数字,在对精度要求极高的科学计算等场景中不可或缺。在实际应用选择时,需充分考虑任务特性、硬件条件等因素,合理运用 FP32 和 FP16,以达到最佳的计算效果。
在未来的发展中,随着对计算性能和资源利用效率要求的不断提高,除了持续优化 FP32 和 FP16 的应用,还可能会涌现出更多新型的浮点精度格式。例如,已经出现的 BF16(脑浮点格式),它同样是 16 位,但在指数位和尾数位的分配上与 FP16 有所不同,在某些特定场景下展现出独特的优势 。相信在众多科研人员和工程师的努力下,浮点运算精度领域将不断创新,为计算机技术的发展注入新的活力,推动各个行业迈向新的高度。
*本文为AI科普文章






