特征降维是数据分析和机器学习中的一个重要步骤,它可以减少数据集中的特征数量,同时尽可能保留原始数据的重要信息。
- 去除冗余信息:降维可以帮助去除数据中的冗余信息,减少特征之间的相关性,从而提高模型的泛化能力。
- 减少计算复杂度:通过降维可以减少特征的数量,从而降低模型的计算复杂度和存储空间需求,加快模型训练和预测的速度。
- 避免过拟合:降维可以减少特征空间的维度,减少模型对训练数据的过拟合风险,提高模型的泛化能力。
- 可视化数据:降维可以将高维数据映射到低维空间,便于可视化展示数据的结构和特征之间的关系。
- 特征选择:降维可以帮助筛选出最具代表性的特征,提高模型的解释性和可解释性。
在实践中,没有一种被认为是完美无缺的特征降维方法。特征降维的困难主要源于如何平衡信息保留和减少维度带来的挑战。
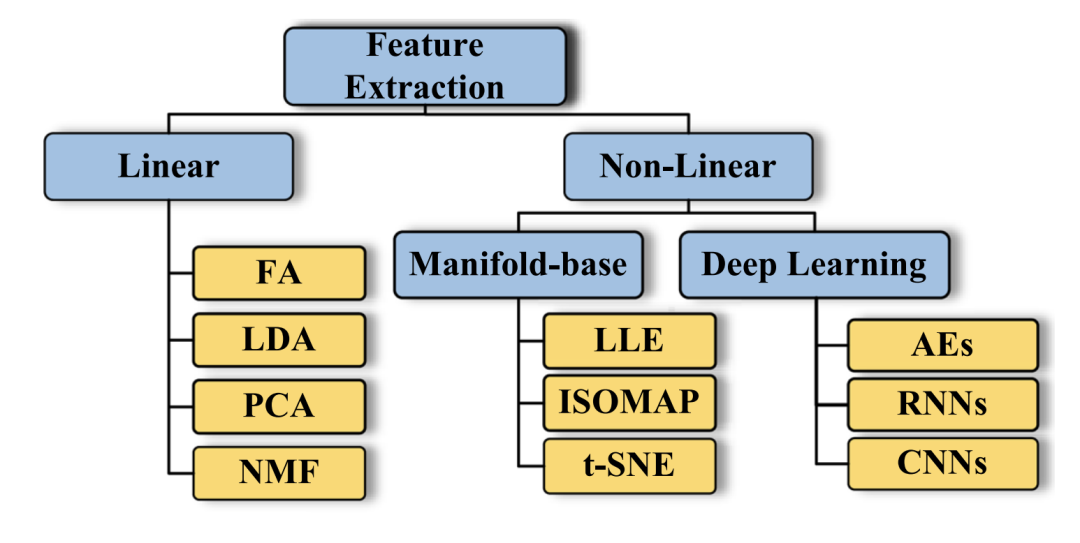
本文讲介绍在Kaggle比赛和日常工作中常见的降维方法,这些方法可以划分为线性降维和非线性降维。
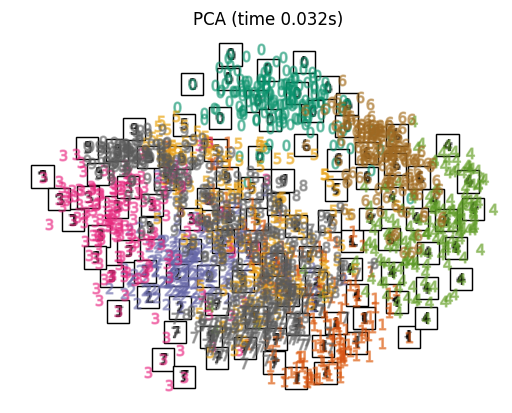
Principal Component Analysis (PCA)
主成分分析(PCA)是一种常用的线性降维方法,用于发现数据中的主要特征,并将数据投影到一个新的低维空间,以保留尽可能多的数据方差。
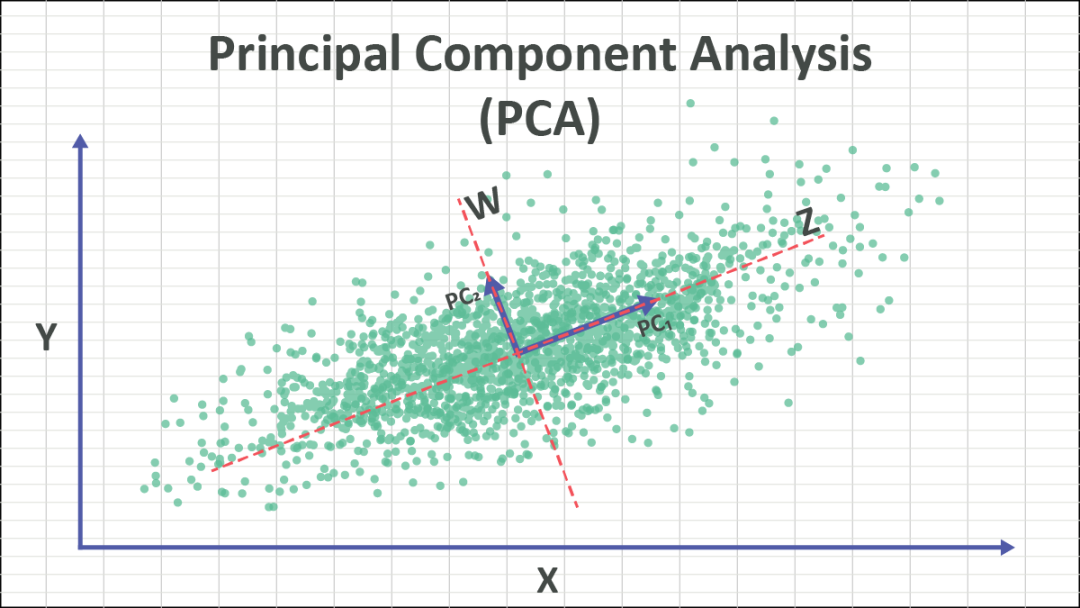
- 主成分(Principal Components):主成分是数据中最具代表性的方向或特征,通过线性变换将数据投影到这些主成分上,可以实现降维。
- 方差(Variance):PCA 的目标是找到能够最大程度保留数据方差的主成分,因为方差代表了数据的信息量。
PCA的计算步骤
- 数据标准化:对原始数据进行标准化处理,使得每个特征的均值为0,方差为1,以消除量纲对结果的影响。
- 计算协方差矩阵:计算标准化后数据的协方差矩阵,该矩阵反映了数据特征之间的相关性。
- 计算特征值和特征向量:通过对协方差矩阵进行特征值分解,得到特征值和对应的特征向量,特征向量即为主成分。
- 选择主成分:按照特征值的大小排序特征向量,并选择最大的k个特征向量作为新的主成分,其中k为降维后的维度。
- 数据投影:将原始数据投影到选定的主成分上,得到降维后的数据集。
| *算法 | 描述 | 适用场景 |
|---|---|---|
| PCA | Principal Component Analysis | 数据降维、数据压缩、去除噪声、数据可视化 |
| IncrementalPCA | Incremental principal components analysis | 处理大型数据集,逐步迭代学习主成分 |
| KernelPCA | Kernel Principal component analysis | 处理非线性数据,使用核技巧进行数据映射 |
| MiniBatchSparsePCA | Mini-batch Sparse Principal Components Analysis | 处理大型数据集,稀疏性数据,加快计算速度 |
| FastICA | Fast Independent Component Analysis | 处理混合信号,盲源分离 |
| SparsePCA | Sparse Principal Components Analysis | 稀疏主成分分析,特征选择和解释性 |
Factor analysis
Factor Analysis(因子分析)是一种统计方法,用于揭示观测数据背后的潜在结构。想象一组观测数据是由一些更简单的隐藏因素或因子所驱动,再加上一些随机噪声的影响。因子分析试图找出这些隐藏因素与观测数据之间的关系。通过分析这些关系,我们可以更好地理解数据背后的模式和结构。
在因子分析中,我们假设这些隐藏因素之间是相互独立的,并且它们的分布通常被假定为高斯分布。通过对观测数据进行分解,我们可以得到载荷矩阵,描述了隐藏因素与观测数据之间的线性关系。Factor Analysis的目标是通过最大似然估计来找到最能解释观测数据变异性的隐藏因素,从而帮助简化数据并发现潜在的模式。
from sklearn.datasets import load_digits from sklearn.decomposition import FactorAnalysis X, _ = load_digits(return_X_y=True) transformer = FactorAnalysis(n_components=7, random_state=0) X_transformed = transformer.fit_transform(X)
Factor Analysis的计算步骤

- 估计载荷矩阵: 通过最大似然估计或其他方法估计描述观测变量与潜在因子关系的载荷矩阵。
- 估计方差: 估计误差方差和潜在因子的方差。
- 选择因子数: 确定最终的因子数和因子载荷,可能需要进行因子旋转等操作。
- 结果应用: 将因子分析结果应用于数据降维、提取数据的潜在结构和模式。
Nonnegative Matrix Factorization (NMF)
NMF(Non-negative Matrix Factorization,非负矩阵分解)采用弗罗贝尼乌斯范数作为距离度量的一种分解方法,假定数据和分量均为非负。NMF可以用于替代PCA或其变体,特别适用于数据矩阵不包含负值的情况。它通过优化样本矩阵的分解为两个非负元素矩阵的距离来实现。

import numpy as np X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]]) from sklearn.decomposition import NMF model = NMF(n_components=2, init='random', random_state=0) W = model.fit_transform(X) H = model.components_
最常用的距离函数是平方弗罗贝尼乌斯范数,它是欧几里德范数对矩阵的明显扩展。与PCA不同,NMF以加法方式获得向量的表示,通过叠加分量而非相减。这种加法模型对于表示图像和文本非常高效。
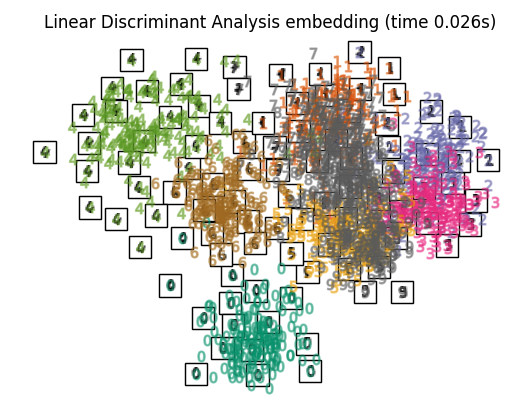
Linear Discriminant Analysis (LDA)
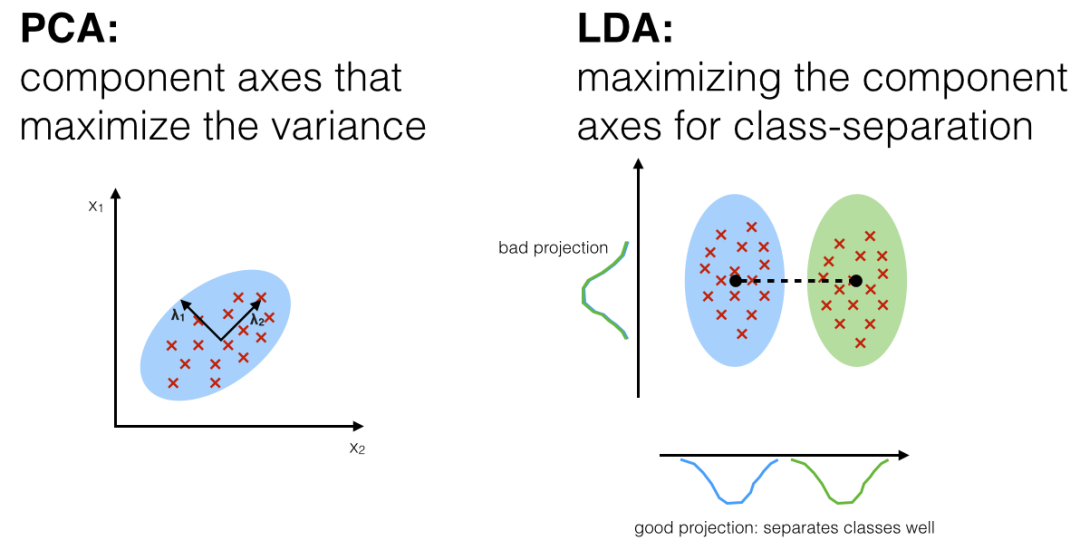
线性判别分析(Linear Discriminant Analysis,LDA)是一种用于降维和分类的监督学习算法。其主要目标是找到一个投影方向,可以最好地分离不同类别的数据点,从而实现有效的分类。
import numpy as np from sklearn.discriminant_analysis import LinearDiscriminantAnalysis X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) y = np.array([1, 1, 1, 2, 2, 2]) clf = LinearDiscriminantAnalysis() clf.fit(X, y)
在LDA中,通过最大化类间距离和最小化类内方差的方式,找到最佳投影方向。具体来说,LDA试图将数据投影到低维空间,同时最大化不同类别之间的距离(类间散度),并最小化相同类别之间的距离(类内散度)。这使得在新空间中,不同类别的数据点更容易区分,提高了分类的准确性。
Isometric Mapping (Isomap)
Isomap(Isometric Mapping)算法是流形学习中最早的方法之一,可以被视为多维缩放(Multi-dimensional Scaling,MDS)或核主成分分析(Kernel PCA)的扩展。Isomap旨在寻找一个保持所有数据点之间测地距离的低维嵌入。
Trees Embedding
RandomTreesEmbedding实现了数据的无监督转换。使用一组完全随机树,RandomTreesEmbedding通过数据点最终所在的叶子节点的索引对数据进行编码。然后这个索引以一种一位有效编码方式进行编码,导致高维稀疏的二进制编码。
from sklearn.ensemble import RandomTreesEmbedding X = [[0,0], [1,0], [0,1], [-1,0], [0,-1]] random_trees = RandomTreesEmbedding( n_estimators=5, random_state=0, max_depth=1).fit(X) X_sparse_embedding = random_trees.transform(X) X_sparse_embedding.toarray()
这种编码可以被非常高效地计算,并可以作为其他学习任务的基础。编码的大小和稀疏性可以通过选择树的数量和每棵树的最大深度来影响。
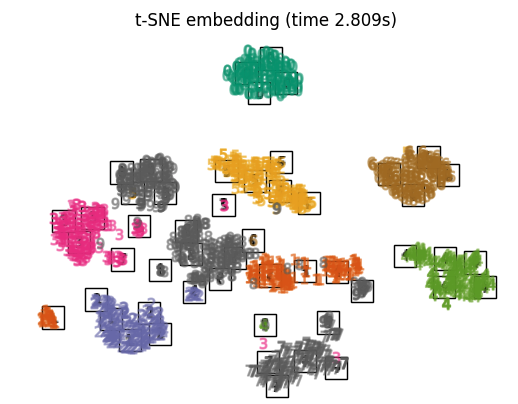
t-distributed Stochastic Neighbour Embedding (t-SNE)
T-分布随机邻域嵌入(T-distributed Stochastic Neighbor Embedding,t-SNE)是一种用于可视化高维数据的工具。它将数据点之间的相似性转换为联合概率,并尝试最小化低维嵌入与高维数据之间的Kullback-Leibler散度。t-SNE具有一个非凸的成本函数,也就是说,使用不同的初始化可能会得到不同的结果。
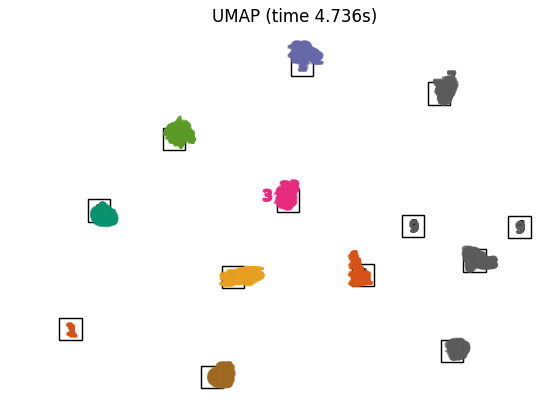
Uniform Manifold Approximation and Projection (UMAP)
UMAP(Uniform Manifold Approximation and Projection)是一种用于降维的技术,类似于t-SNE,可用于数据可视化,同时也适用于一般的非线性降维。该算法基于对数据的三个假设:
1. 数据在黎曼流形上均匀分布;
2. 黎曼度量在局部是恒定的(或可以近似为恒定);
3. 流形在局部是连通的。

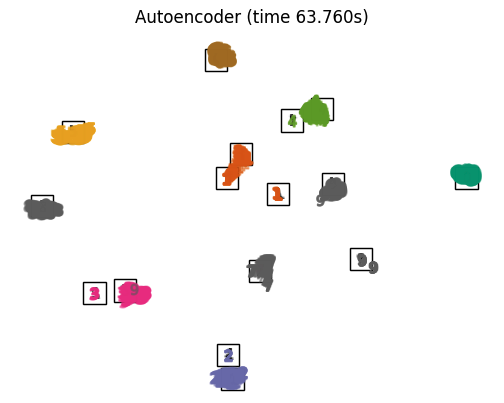
AutoEncoder (AE)
自编码器(Autoencoder)是一种无监督学习的神经网络模型,通常用于数据压缩、降维、特征学习等任务。它由一个编码器(Encoder)和一个解码器(Decoder)组成,通过将输入数据压缩成低维表示(编码)然后再恢复成原始数据(解码)来学习数据的有效表示。自编码器的训练过程旨在最小化重构误差,即使得解码器输出的数据尽可能接近输入数据。这种无监督学习的方式有助于自编码器学习数据的潜在结构和特征。
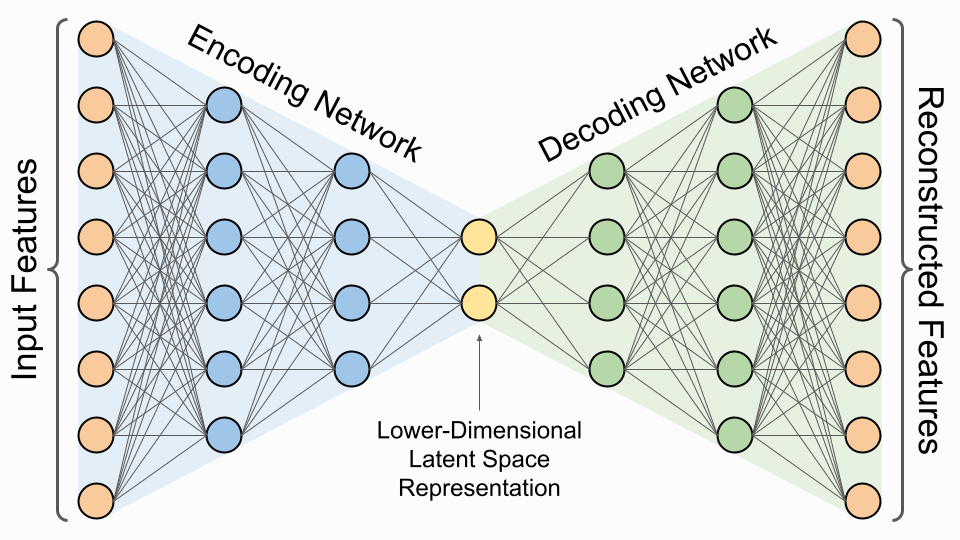
- 稀疏自编码器(Sparse Autoencoder):在损失函数中加入稀疏性约束,鼓励模型学习到稀疏的表示,有助于学习更加鲁棒和有意义的特征。
- 降噪自编码器(Denoising Autoencoder):通过向输入数据添加噪声,强制自编码器学习对噪声具有鲁棒性的表示,有助于提高模型的泛化能力。
- 变分自编码器(Variational Autoencoder,VAE):与传统自编码器不同,VAE学习数据的潜在分布,使得生成的数据更具有连续性,常用于生成模型和潜在变量建模。
不同方法效果对比
原始数据
digits = load_digits(n_class=10)
X, y = digits.data, digits.target
fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6))
for idx, ax in enumerate(axs.ravel()):
ax.imshow(X[idx].reshape((8, 8)), cmap=plt.cm.binary)
ax.axis("off")
_ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16)不同降维方法
本文转自:Coggle数据科学,转载此文目的在于传递更多信息,版权归原作者所有。如不支持转载,请联系小编demi@eetrend.com删除。






