表格数据的特征工程
表格数据的特征工程本是一个模块化过程,目标是对数据集进行编码以获得更好的模型精度。
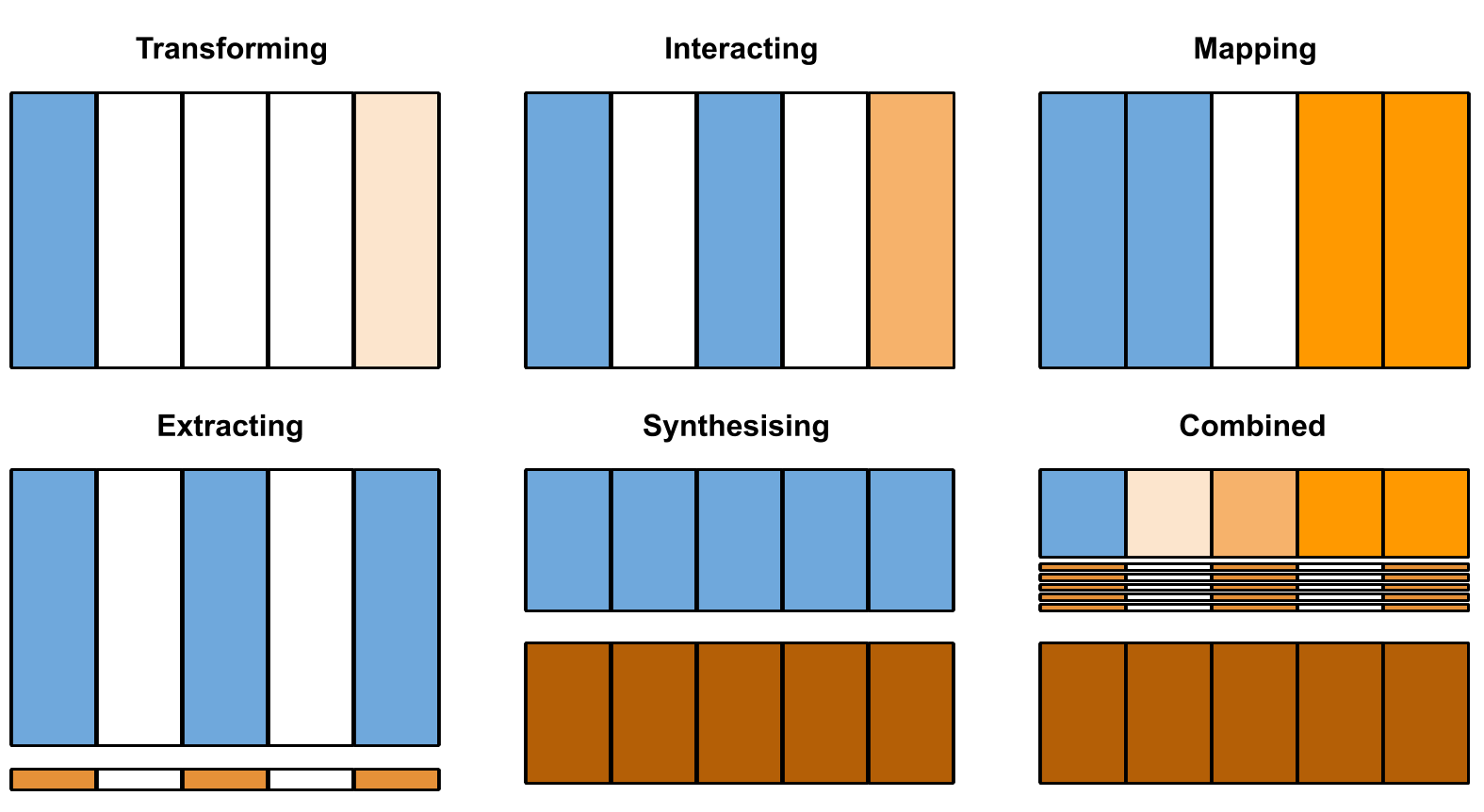
如果想要充分提取表格数据的特征,可以顺序执行技术:
1. 特征转换 (Transforming): 对数据进行转换,例如标准化、归一化或对数变换,以消除数据的非线性关系和不稳定性。
2. 特征交互 (Interacting): 创建新的特征,通过对现有特征进行交互操作,例如特征组合、交叉乘积等,以捕获特征之间的关联性。
3. 特征映射 (Mapping): 将原始数据映射到新的特征空间,可以利用降维技术如主成分分析 (PCA) 或 t-SNE,以减少特征维度并保留数据的重要信息。
4. 特征提取 (Extracting): 从原始数据中提取更多有用的信息,例如从时间序列中提取趋势、周期性、季节性等特征。
5. 特征合成 (Synthesising): 使用合成技术生成新的数据样本,例如基于生成对抗网络 (GANs) 的数据生成,以扩充数据集并提高模型的泛化能力。
特征转换
转换是指任何仅使用一个特征作为输入来生成新特征的方法。转换可以应用于横截面和时间序列数据。一些转换方法仅适用于时间序列数据(如平滑、过滤),但也有少数方法适用于两种类型的数据。
▎缩放
缩放会应用于整个数据集,对于某些算法尤其必要。K均值利用欧几里得距离,因此需要缩放。对于PCA,因为我们试图识别具有最大方差的特征,所以也需要缩放。
缩放方法包括:
- 最小-最大缩放器
- 最大绝对值缩放器
- 鲁棒缩放器
▎标准化
当属性本身服从高斯分布时,通常模型更有效。此外如果使用的模型假设为高斯分布时,例如线性回归、逻辑回归和线性判别分析,标准化也是必要的。
标准话方法包括:
- 标准化方法
- 非线性方法
▎设置范围
封顶是指对特征值设置一个下限和一个上限的任何方法。可以通过使用平均值、最大值和最小值,或任意极端值来对值进行封顶。
▎数值变换
变换被视为传统转换的一种形式。它是将一个变量替换为该变量的函数。在更强的意义上,转换是一种改变分布或关系形状的替换。
- 特征减去各自的最小值
- 计算特征的平方
- 计算特征的绝对值加一的自然对数
- 计算特征加一的倒数
- 计算特征的绝对值加一的平方根
▎时序差分
差分是指计算连续观测值之间的差异,通常用于获取平稳的时间序列。通过计算连续观测值之间的差异,可以将非平稳的时间序列转换为平稳的时间序列。平稳的时间序列更容易建立模型和进行预测分析。
▎时序平滑
平滑的主要目的是消除数据中的噪声或波动,从而使数据更易于分析和解释。例如简单移动平均和单、双和三重指数平滑方法。
▎时序分解
分解时间序列是一种常见的统计方法,旨在将时间序列数据拆分为趋势、季节性和残差(随机性)等组成部分,以便更好地理解和分析数据的特征。
- 趋势(Trend):表示数据长期变化的趋势,可以是逐渐上升或下降的模式。
- 季节性(Seasonality):表示数据在特定时间段内重复出现的周期性模式,例如每年、每季度或每月的季节性变化。
- 残差(Residuals):表示除了趋势和季节性之外的随机波动或未解释的部分。
▎滚动计算(Rolling)
滚动计算是指基于固定窗口大小的滚动基础上计算的特征。
- 遍历每个指定的窗口大小。
- 对每个窗口大小,计算滚动窗口内数据的统计函数,如平均值、标准差等。
- 对计算结果重命名列名,以表示窗口大小。
- 将原始数据框和滚动计算的结果连接起来,返回包含所有特征的新数据框。
▎滞后特征(Lags)
滞后值是指基于现有特征的延迟值。
- 对于指定的滞后值范围(从 start 到 end),遍历每个滞后值。
- 对于每个滞后值和每个指定的列,使用 shift 函数将特征值向后移动,生成滞后值。
特征交互
特征交互是使用多于一个特征来创建额外特征的方法。交互作用方法的一个例子是将两个特征相乘,以创建一个新的特征,表示这两个特征之间的相互影响。
▎数值计算
在特征之间进行交互操作的一种常见方法是使用乘法、除法、加法和减法。
- 量纲相同的特征之间可以加、减和除
- 量纲不同的特征自检可以乘和除
▎分组聚合
分组聚合是指根据某些特征将数据分组,然后在每个组内对数据进行聚合操作,以生成新的特征。
▎决策树编码
在决策树离散化中,决策树被用来找到最佳的分割点,以将连续的特征值划分为不同的离散区间。
特征映射
映射方法是一种将特征进行重新映射以达到某种目的的技术。这些目的可能包括最大化变异性、增加类别可分性等。映射方法通常是无监督的,但也可以采用监督形式。
▎主成分分析(Principal Component Analysis,PCA)
PCA通过线性变换将原始数据转换为一组线性无关的变量,称为主成分。PCA的目标是找到能够最大化数据方差的投影方向,从而实现数据的降维。
主成分通常是原始特征的线性组合,每个主成分都是彼此正交的,并且它们的方差逐渐减小。PCA可用于去除数据中的冗余信息,并减少特征的数量,同时保留最重要的信息。
▎Canonical Correlation Analysis (CCA)
CCA是一种多变量数据分析方法,用于探索两个数据集之间的线性关系。它通过分析两个数据集之间的相关性,找到它们之间最大化的相关性模式。
CCA 的目标是找到一组线性变换,使得在新的特征空间中,两个数据集之间的相关性达到最大。
▎Autoencoder(自编码器)
自编码器是一种人工神经网络,用于以无监督的方式学习数据的高效编码。自编码器的目标是通过训练网络忽略噪声,学习一组数据的表示(编码),通常用于降低数据的维度。
自编码器可以学习数据的紧凑表示,从而在保留重要特征的同时,去除数据中的噪声和冗余信息。
▎流形学习(Manifold Learning)
流形学习能够有效地处理非线性结构的数据,并且相对于某些其他降维方法,它能更好地保持数据的局部结构和流形特征。
▎特征凝聚(Feature Agglomeration)
Feature Agglomeration 可以将数据中高度相关的特征合并成一个新的特征或特征组,从而降低数据的维度。
▎邻近点(Nearest Neighbor)
邻近点方法是一种基于距离度量的机器学习方法,它利用距离度量(如汉明距离、曼哈顿距离、闵可夫斯基距离等)来寻找与新数据点最接近的预定义数量的训练样本,并根据这些样本来编码当前样本。
特征提取
特征提取阶段涉及从时间序列数据中提取有意义的特征或特性。这些特征可以捕获数据中的重要模式、趋势或信息,然后可以用于建模或分析目的。
1. 绝对能量:衡量时间序列数据的总体能量。
2. CID特征:用于计算时间序列的复杂度。
3. 平均绝对变化:时间序列数据的平均绝对变化量。
4. 平均二阶中心导数:时间序列的平均二阶导数。
5. 方差大于标准差的值:检查时间序列数据中方差是否大于标准差。
6. 方差指数:衡量时间序列数据中的方差指数。
7. 对称性检查:检查时间序列数据的对称性。
8. 是否存在重复的最大值:检查时间序列数据中是否存在重复的最大值。
9. 局部自相关:计算时间序列数据的局部自相关性。
10. 增广迪基-富勒检验:用于检验时间序列数据的平稳性。
11. 斜度峰度:衡量时间序列数据的斜度和峰度。
12. 斯泰特森均值:计算时间序列数据的斯泰特森均值。
13. 长度:时间序列数据的长度。
14. 高于平均值的计数:统计时间序列数据中高于平均值的数量。
15. 低于平均值的最长连续段:计算时间序列数据中低于平均值的最长连续段。
16. Wozniak特征:一种特征提取方法。
17. 最大值的最后位置:时间序列数据中最大值的最后出现位置。
18. 傅立叶变换系数:对时间序列数据进行傅立叶变换,获取其频谱特征。
本文转自:Coggle数据科学,转载此文目的在于传递更多信息,版权归原作者所有。如不支持转载,请联系小编demi@eetrend.com删除。






