一、 特征选择的意义
约简冗余,不相关,噪声和无信息数据,减少存储空间,降低时间复杂度,同时维度降低有助于缓解过拟合问题,即缓慢和过拟合这两个相互交织的问题都可以通过特征缩减来解决,其目标是最小化用于执行二元分类任务的维数。
二、特征选择的方法
1. 排序方法(Ranking methods)
排序方法,也称为个体特征评估或特征加权技术,独立评估每个特征的信息量,并根据它们的相关性程度分配它们的权重。对单个特征计算信息增益、相关系数、卡方统计、信号-噪声统计等几种评价指标,以获得基于其个体评价的排序。然后,通过建立阈值截断,选择秩值最高的特征,获得有效的特征子集。
缺点:只能消除不相关的特性,而不能消除冗余的特性。
优点:这些单变量技术非常简单,但它们的性能可以与多变量方法竞争
2. 过滤方法(Filter approaches)
过滤方法,也被称为分类器独立的方法。它独立于任何归纳算法,基于距离、信息、依赖性和一致性四种不同的评价标准进行评价,利用数据的内在特征对特征进行评价和排序,根据训练数据的共同特征来选择合适的特征,而不涉及任何特定的学习器。
基于滤波器的方法可以分为单变量方法和多变量方法。在单变量中,特征的重要性是单独计算的,而忽略了特征之间的关系,而在多变量中,将考虑特征的相互作用和依赖关系。其优点是速度快、计算简单、经济,更适合于解决高维数据集问题。
最流行的为特征相关性进行评分的标准之一是皮尔逊相关系数,计算公式为:
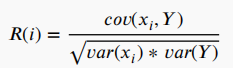
其中,Xi为第 i 个特征,Y为类标签,cov()为协方差,var()为方差。该准则只能检测变量与目标之间的线性依赖关系。
信息理论排序标准,如将互信息(MI)作为两个变量之间依赖性的度量,X和Y之间的MI值为:
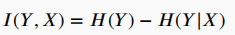
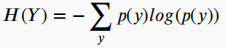
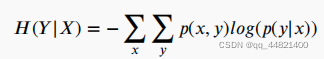
其中,H(Y)为香农熵,H(Y|X)是输出Y的条件熵,如果Y和X是独立的,那么MI值为零,否则MI大于零。
3. 包装器方法(wrapper methods)
通过迭代搜索整个特征空间,生成候选特征子集,将优化一个特定分类器的性能度量,这种性能度量或目标函数取决于问题的类型。例如,回归评价标准可以是r-平方,而分类评价标准可以是准确性、查全率、精确度、f1-分数等。用于包装器特征选择的常用搜索算法包括分支和绑定方法和几种元启发式算法。除了启发式搜索算法外,一些包装器特征选择方法还基于顺序选择算法,如顺序前向选择(SFS)、顺序后向选择(SBS)、顺序前向浮动选择(SFFS)和顺序后向浮动选择(SBFS)。这些方法迭代地添加或删除特征,直到满足终止标准。
缺点:计算复杂度随着特征空间的增长而增加。
优点:由于特征选择针对特定的学习算法进行优化,不包含关于特定结构的分类或回归函数的知识,因此可以与任何学习机器结合。
4. 混合方法(Hybrid methods)
在单个上下文中同时利用过滤器方法和包装器方法,以提高FS算法。
5. 嵌入式方法(Embedded methods)
指那些直接将特征选择作为分类算法优化目标的方法,寻求在学习算法中加入特征选择能力,即在训练和建立归纳模型的过程中进行特征选择。计算成本较低,也不太容易发生过拟合。如使用分类器的权重进行特征排序,权重 Wj 定义为
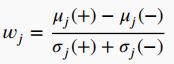
其中 uj和 σj为(+)和(-)类样本的平均值和标准差。较大的正 Wj 值表示与类(+)有很强的相关性,而较大的负 Wj 值表示与类(-)有很强的相关性。
一些嵌入式方法涉及到改变分类器的目标函数,以学习使用模型权重向量的特征排序。例如,修改支持向量机(SVM)的成本函数,以执行递归特征消除(RFE)的方法被称为SVM-RFE方法,类似的技术已经被开发出来用于多层神经网络。
版权声明:本文为CSDN博主「qq_44821400」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_44821400/article/details/123496328






