图形学——光栅化

光栅化概述

raster: screen
rasterize: draw onto the screen

我们往往是通过光栅化三角形来得到更复杂的图形

三角形的优秀性质：
① 最基本的多边形
② 其他多边形可以拆成多个三角形
③ 三角形一定在一个平面上
④ 三角形的内部和外部分的很清楚
⑤ 有好的方法用于在三角形内部插值

光栅化的方法

在视图变换之后，想要把一个canonical cube，即[−1,1]3的方块，放到屏幕上，我们先忽略z方向，进行以下操作
1. 把cube的xy平面缩放到width*height
2. 把cube的xy平面左下角放到原点

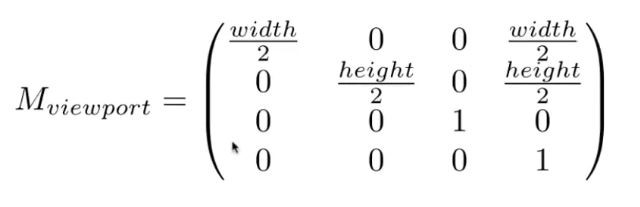
光栅化的重点：
判断像素中心点与三角形的关系，在三角形内部的我们就将像素染色

方法：采样

采样的定义：
将一个函数离散化，也就是通过在函数上取特定的点得到点的函数值

我们在屏幕空间上的采样：
判断每个像素的中心是否在三角形内部，得到一个inside函数，得到每一个像素的值是0还是1

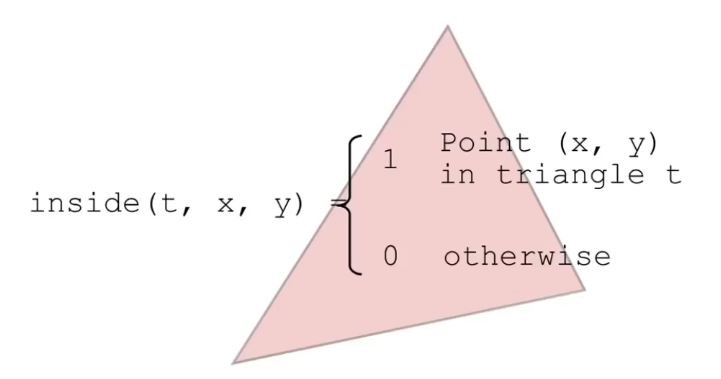
这就是对一个三角形光栅化的过程

具体判断是否在三角形内部，我们用叉乘的方式来判断

我们从任何一个点开始，按顺序叉乘，先是P1P2叉乘P1Q，再是P2P0叉乘P2Q，最后是P0P1叉乘P0Q，得到的三个结果如果全是正的，或者全是负的，则证明点Q落在三角形内部，否则不是

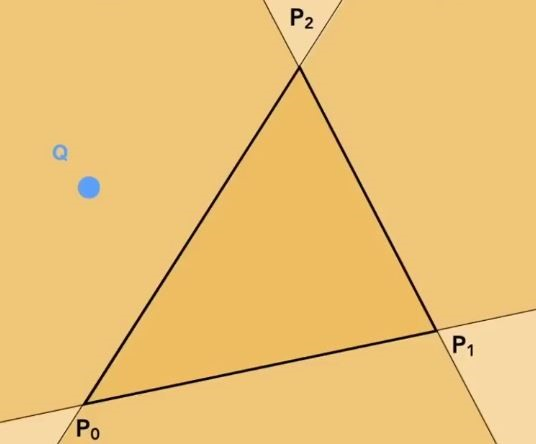
对于落在边上的点，视情况处理

光栅化的加速

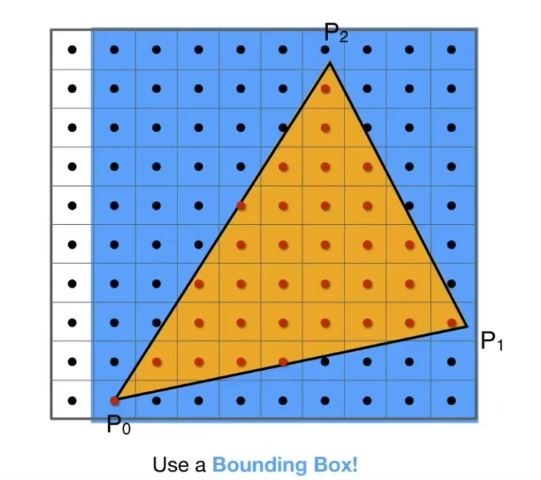
① 包围盒bounding box，对边界进行简单判断，取一个矩形，矩形之外的像素不需要光栅化

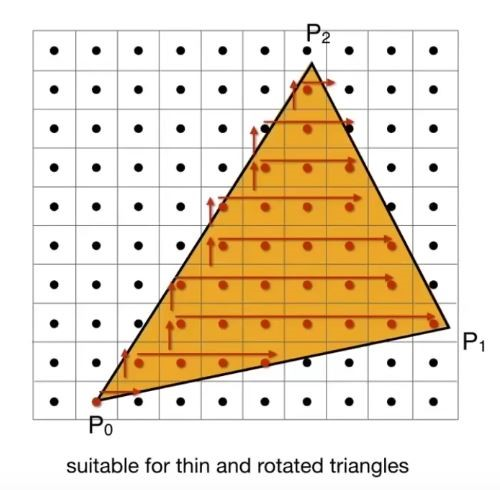
② 逐行判断，对每一行都判断边界，这种方法适用于斜过来而窄长的三角形，Bounding box会太大

真实的光栅化

每个像素点都是三原色组成，在S5中用的是Bayer-Pattern，并不是一个方形

---

本文转自：wcvanvan's house，转载此文目的在于传递更多信息，版权归原作者所有。如不支持转载，请联系小编demi@eetrend.com删除。