来源:DeepHub IMBA
作者:Gleb Kumichev
本文中将研究如何基于消息传递机制构建图卷积神经网络,并创建一个模型来对具有嵌入可视化的分子进行分类。
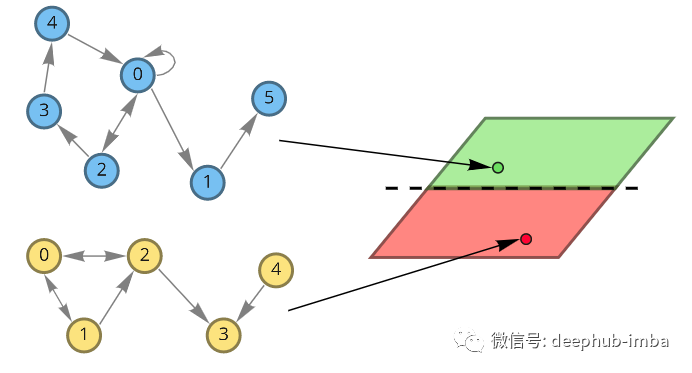
假设现在需要设计治疗某些疾病的药物。有一个其中包含成功治疗疾病的药物和不起作用的药物数据集,现在需要设计一种新药,并且想知道它是否可以治疗这种疾病。如果可以创建一个有意义的药物表示,就可以训练一个分类器来预测它是否对疾病治疗有用。我们的药物是分子式,可以用图表表示。该图的节点是原子。也可以用特征向量 x 来描述原子(它可以由原子属性组成,如质量、电子数或其他)。为了对分子进行分类,我们希望利用有关其空间结构和原子特征的知识来获得一些有意义的表示。
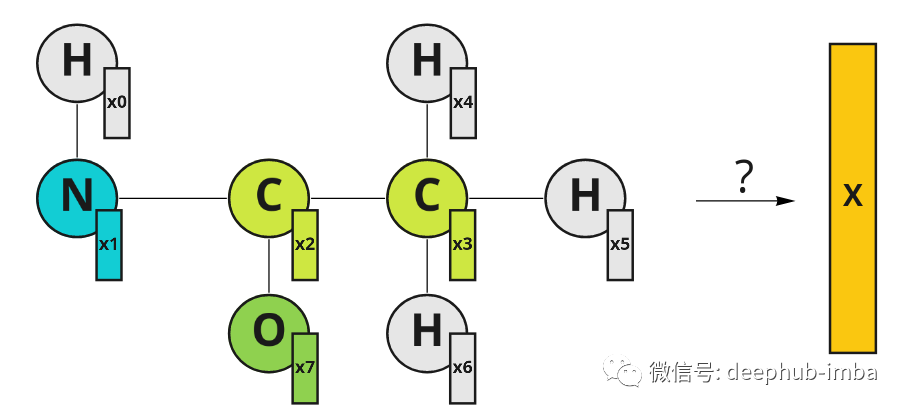
以图形表示的分子示例。原子有它们的特征向量 X。特征向量中的索引表示节点索引。
最直接的方法是聚合特征向量,例如,简单地取它们的平均值:
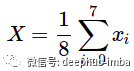
这是一个有效的解决方案,但它忽略了重要的分子空间结构。
图卷积
我们可以提出另一种想法:用邻接矩阵表示分子图,并用特征向量“扩展”其深度。我们得到了一个伪图像 [8, 8, N],其中 N 是节点特征向量 x 的维数。现在可以使用常规卷积神经网络并提取分子嵌入。
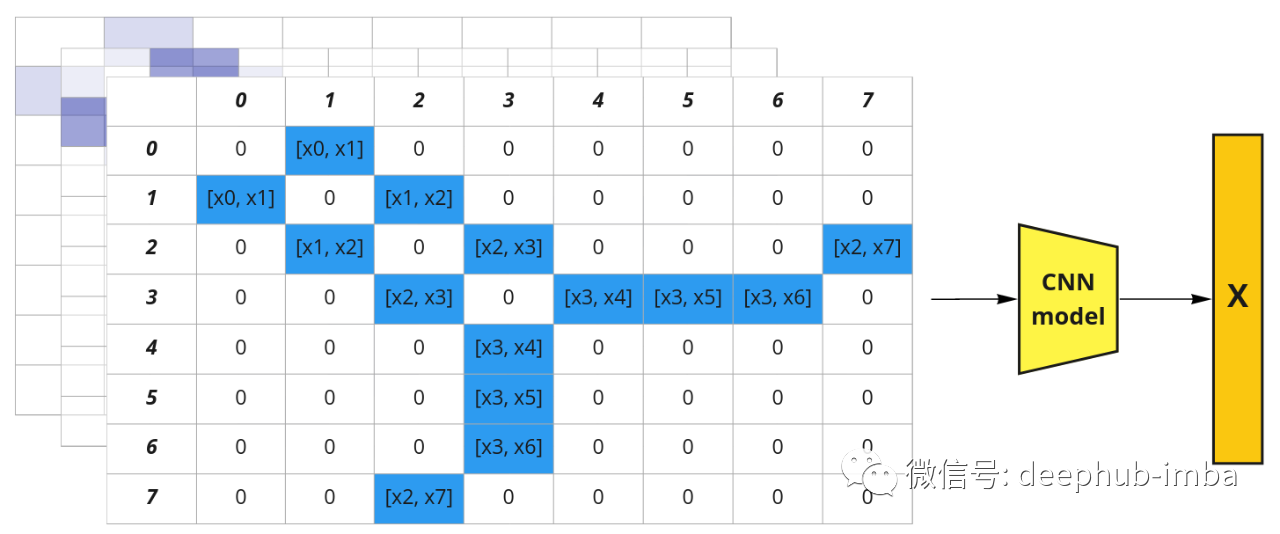
图结构可以表示为邻接矩阵。节点特征可以表示为图像中的通道(括号代表连接)。
这种方法利用了图结构,但有一个巨大的缺点:如果改变节点的顺序会得到不同的表示。所以这样的表示不是置换不变量。但是邻接矩阵中的节点顺序是任意的, 例如,可以将列顺序从 [0, 1, 2, 3, 4, 5, 6, 7] 更改为 [0, 2, 1, 3, 5, 4, 7, 6],它仍然是 图的有效邻接矩阵。所以可以创建所有可能的排列并将它们堆叠在一起,这会使我们有 1625702400 个可能的邻接矩阵(8!* 8!)。数据量太大了,所以应该找到更好的解决方案。
但是问题是,我们如何整合空间信息并有效地做到这一点?上面的例子可以让我们想到卷积的概念,但它应该在图上完成。
所以图卷积就出现了
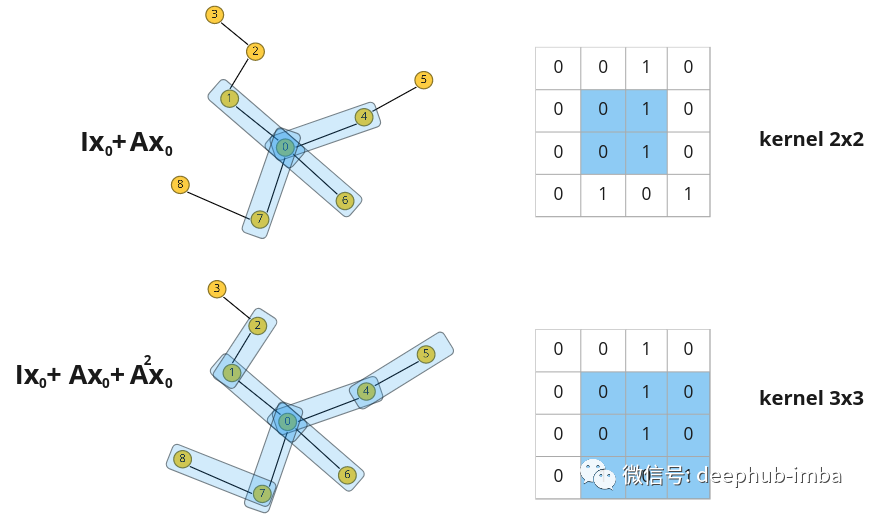
当对图像应用常规卷积时会发生什么?相邻像素的值乘以过滤器权重并相加。我们可以在图表上做类似的事情吗?是的,可以在矩阵 X 中堆叠节点特征向量并将它们乘以邻接矩阵 A,然后得到了更新的特征 X`,它结合了有关节点最近邻居的信息。为简单起见,让我们考虑一个具有标量节点特征的示例:
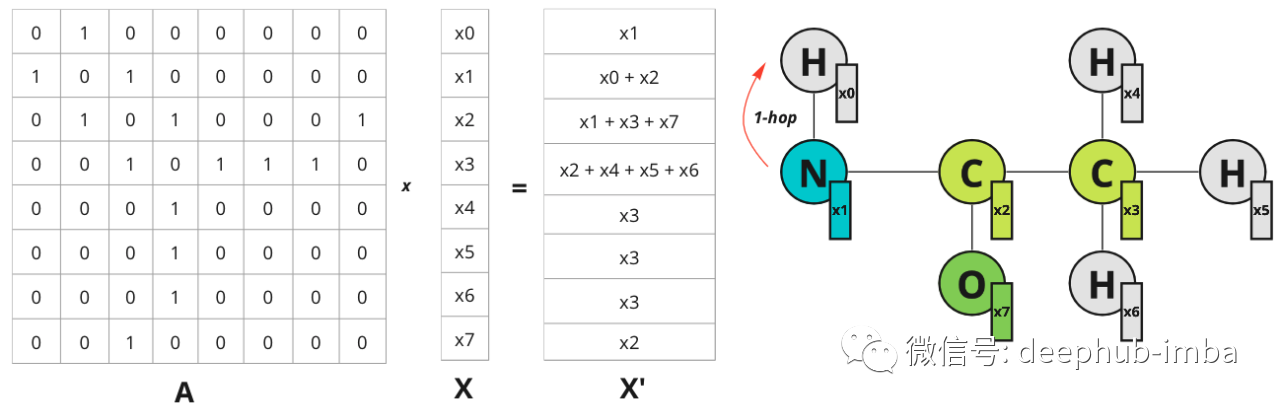
标量值节点特征的示例。仅针对节点 0 说明了 1 跳距离,但对于所有其他节点也是一样的。
每个节点都会获得有关其最近邻居的信息(也称为 1 跳距离)。邻接矩阵上的乘法将特征从一个节点传播到另一个节点。
在图像域中可以通过增加滤波器大小来扩展感受野。在图中则可以考虑更远的邻居。如果将 A^2 乘以 X——关于 2 跳距离节点的信息会传播到节点:
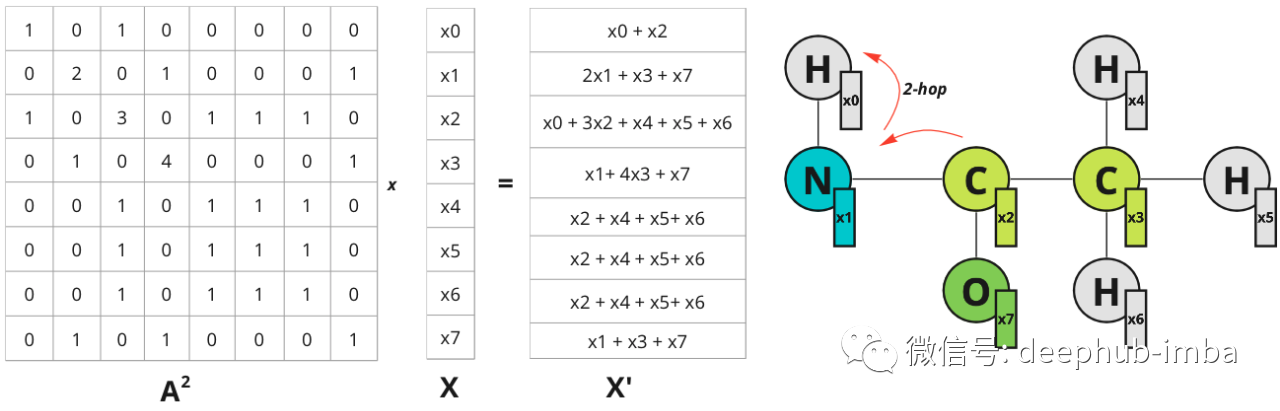
节点 0 现在具有关于节点 2 的信息,该信息位于 2 跳距离内。该图仅针对节点 0 说明了跃点,但对于所有其他节点也是如此。
矩阵 A 的更高幂的行为方式相同:乘以 A^n 会导致特征从 n 跳距离节点传播,所以可以通过将乘法添加到邻接矩阵的更高次方来扩展“感受野”。为了概括这一操作,可以将节点更新的函数定义为具有某些权重 w 的此类乘法之和:
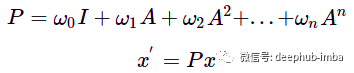
多项式图卷积滤波器。A——图邻接矩阵,w——标量权重,x——初始节点特征,x'——更新节点特征。
新特征 x' 是来自 n 跳距离的节点的某种混合,相应距离的影响由权重 w 控制。这样的操作可以被认为是一个图卷积,滤波器 P 由权重 w 参数化。与图像上的卷积类似,图卷积滤波器也可以具有不同的感受野并聚合有关节点邻居的信息,但邻居的结构不像图像中的卷积核那样规则。
这样的多项式与一般卷积一样是置换等变性的。可以使用图拉普拉斯算子而不是邻接矩阵来传递特征差异而不是节点之间的特征值(也可以使用标准化的邻接矩阵)。
将图卷积表示为多项式的能力可以从一般的谱图卷积( spectral graph convolutions)中推导出来。例如,利用带有图拉普拉斯算子的切比雪夫多项式的滤波器提供了直接谱图卷积的近似值 [1]。
并且可以轻松地将其推广到具有相同方程的节点特征的任何维度上。但在更高维度的情况下,处理的是节点特征矩阵 X 而不是节点特征向量。例如,对于 N 个节点和节点中的 1 或 M 个特征,我们得到:
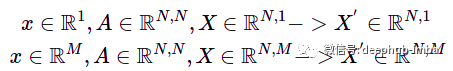
x——节点特征向量,X——堆叠节点特征,M——节点特征向量的维度,N——节点数量。
可以将特征向量的“深度”维度视为图像卷积中的“通道”。
消息传递
现在用另外一种不同的方式看看上面的讨论。继续采用上面讨论的一个简单的多项式卷积,只有两个第一项,让 w 等于 1:
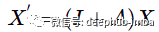
现在如果将图特征矩阵 X 乘以 (I + A) 可以得到以下结果:
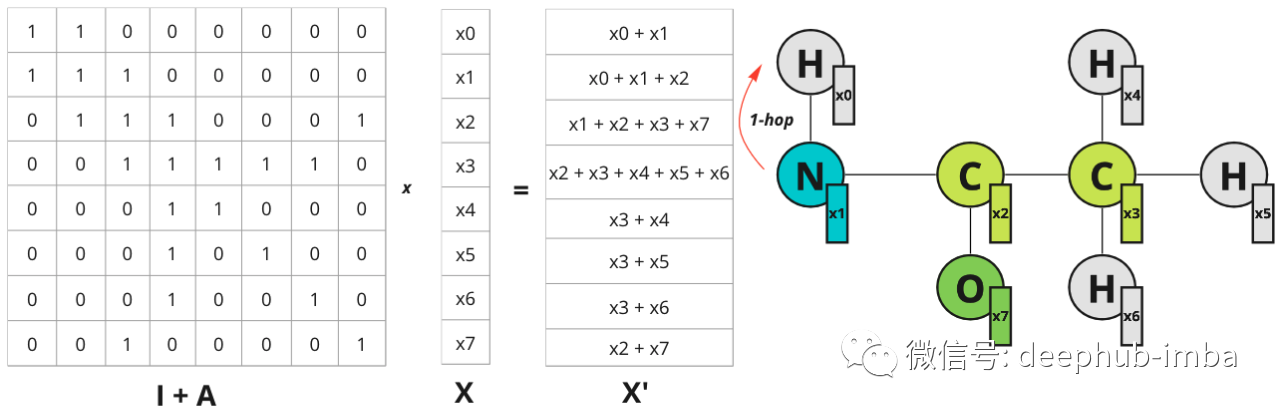
对于每个节点,都添加了相邻节点的总和。因此该操作可以表示如下:
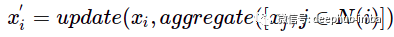
N(i) 表示节点 i 的一跳距离邻居。
在这个例子中,“update”和“aggregate”只是简单的求和函数。
这种关于节点特征更新被称为消息传递机制。这样的消息传递的单次迭代等效于带有过滤器 P= I + A 的图卷积。那么如果想从更远的节点传播信息,我们可以再次重复这样的操作几次,从而用更多的多项式项逼近图卷积。
但是需要注意的是:如果重复多次图卷积,可能会导致图过度平滑,其中每个节点嵌入对于所有连接的节点都变成相同的平均向量。
那么如何增强消息传递的表达能力?可以尝试聚合和更新函数,并额外转换节点特征:
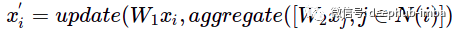
W1——更新节点特征的权重矩阵,W2——更新相邻节点特征的权重矩阵。
可以使用任何排列不变函数进行聚合,例如 sum、max、mean 或更复杂的函数,例如 DeepSets。
例如,评估消息传递的基本方法之一是 GCN 层:
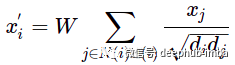
第一眼看到这个公式可能并不熟悉,但让我们使用“更新”和“聚合”函数来看看它:
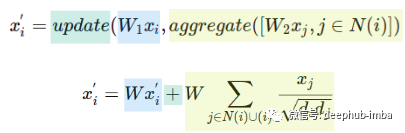
使用单个矩阵 W 代替两个权重矩阵 W1 和 W2。更新函数是求和,聚合函数是归一化节点特征的总和,包括节点特征 i。d——表示节点度。
这样就使用一个权重矩阵 W 而不是两个,并使用 Kipf 和 Welling 归一化求和作为聚合,还有一个求和作为更新函数。聚合操作评估邻居和节点 i 本身,这相当于将自循环( self-loops)添加到图中。
所以具有消息传递机制的 GNN 可以表示为多次重复的聚合和更新函数。消息传递的每次迭代都可以被视为一个新的 GNN 层。节点更新的所有操作都是可微的,并且可以使用可以学习的权重矩阵进行参数化。现在我们可以构建一个图卷积网络并探索它是如何执行的。
一个实际的例子
使用上面提到的 GCN 层构建和训练图神经网络。对于这个例子,我将使用 PyG 库和 [2] 中提供的 AIDS 图数据集。它由 2000 个代表分子化合物的图表组成:其中 1600 个被认为对 HIV 无活性,其中 400 个对 HIV 有活性。每个节点都有一个包含 38 个特征的特征向量。以下是数据集中分子图表示的示例:
使用 networkx 库可视化来自 AIDS 数据集的样本。
为简单起见,我们将构建一个只有 3 个 GCN 层的模型。嵌入空间可视化的最终嵌入维度将是 2-d。为了获得图嵌入,将使用均值聚合。为了对分子进行分类,将在图嵌入之后使用一个简单的线性分类器。
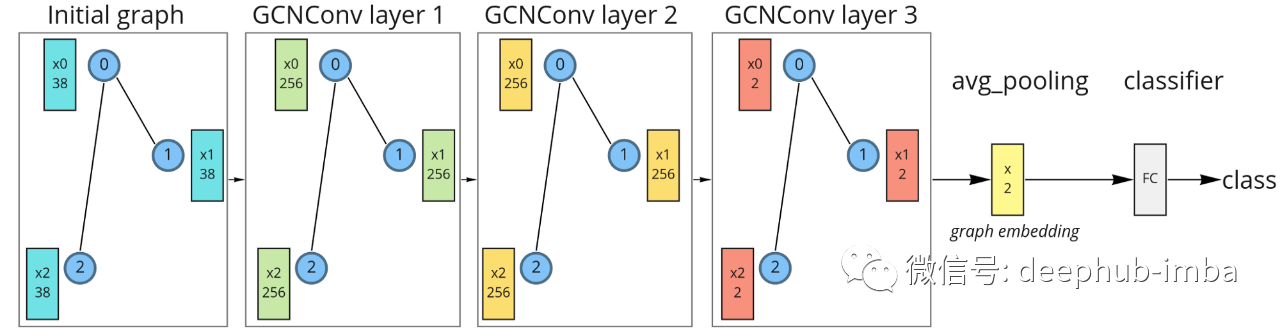
具有三个 GCN 层、平均池化和线性分类器的图神经网络。
对于第一次消息传递的迭代(第 1 层),初始特征向量被投影到 256 维空间。在第二个消息传递期间(第 2 层),特征向量在同一维度上更新。在第三次消息传递(第 3 层)期间,特征被投影到二维空间,然后对所有节点特征进行平均以获得最终的图嵌入。最后,这些嵌入被输送到线性分类器。选择二维维度只是为了可视化,更高的维度肯定会更好。这样的模型可以使用 PyG 库来实现:
from torch import nn
from torch.nn import functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.nn import global_mean_pool
class GCNModel(nn.Module):
def __init__(self, feature_node_dim=38, num_classes=2, hidden_dim=256, out_dim=2):
super(GCNModel, self).__init__()
torch.manual_seed(123)
self.conv1 = GCNConv(feature_node_dim, hidden_dim)
self.conv2 = GCNConv(hidden_dim, hidden_dim)
self.conv3 = GCNConv(hidden_dim, out_dim)
self.linear = nn.Linear(out_dim, num_classes)
def forward(self, x, edge_index, batch):
# Graph convolutions with nonlinearity:
x = self.conv1(x, edge_index)
x = F.relu(x)
x = self.conv2(x, edge_index)
x = F.relu(x)
x = self.conv3(x, edge_index)
# Graph embedding:
x_embed = global_mean_pool(x, batch)
# Linear classifier:
x = self.linear(x_embed)
return x, x_embed在其训练期间,可以可视化图嵌入和分类器决策边界。可以看到消息传递操作如何使仅使用 3 个图卷积层的生成有意义的图嵌入的。这里使用随机初始化的模型嵌入并没有线性可分分布:
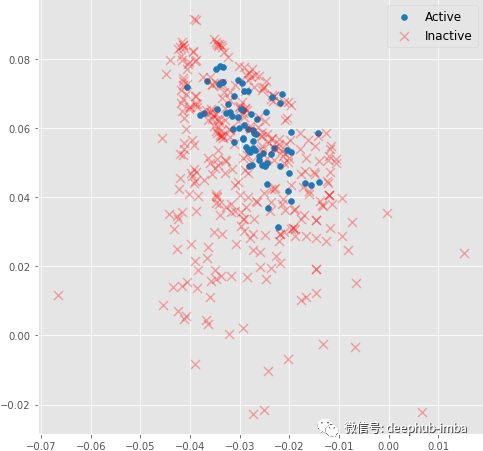
上图是对随机初始化的模型进行正向传播得到的分子嵌入
但在训练过程中,分子嵌入很快变成线性可分:
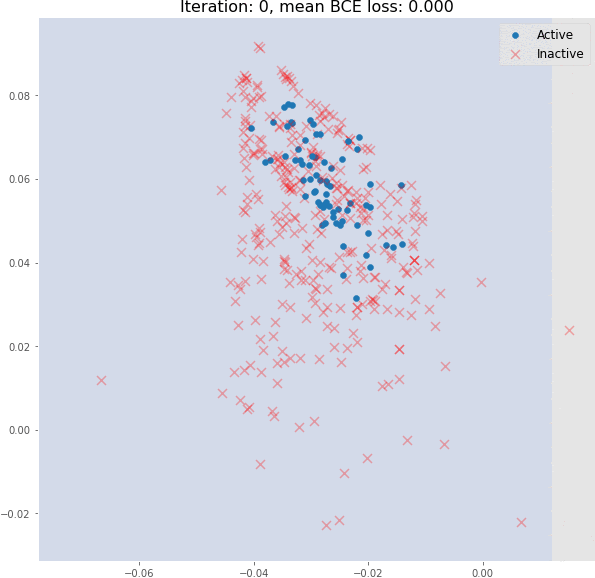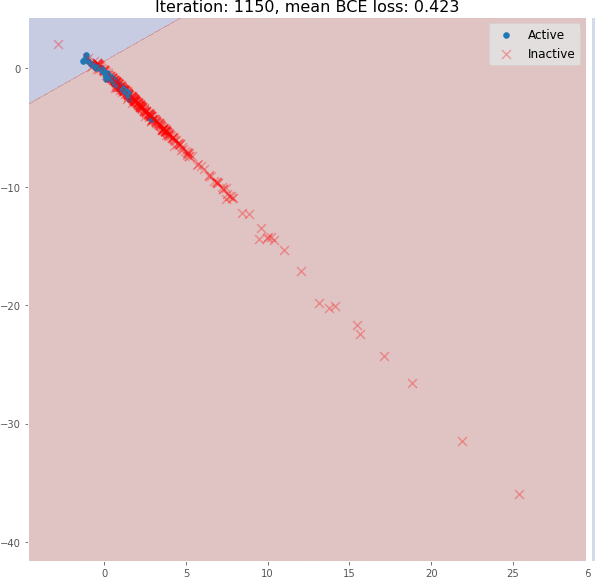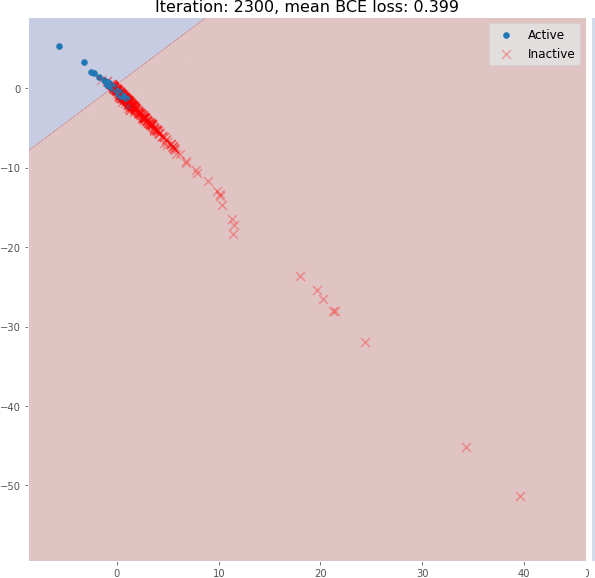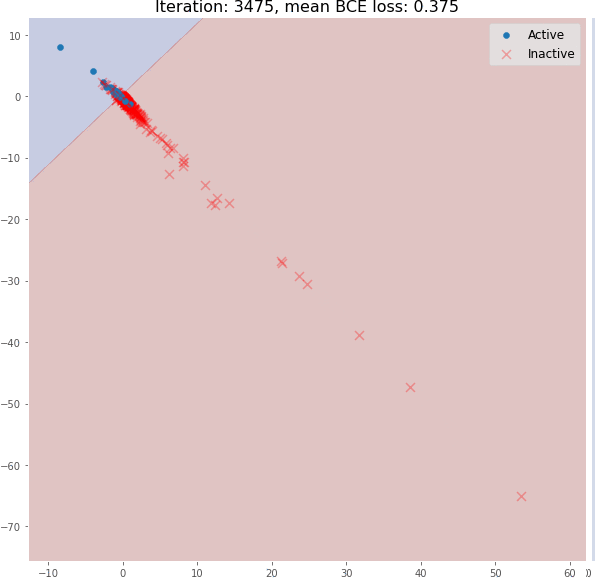
即使是 3 个图卷积层也可以生成有意义的二维分子嵌入,这些嵌入可以使用线性模型进行分类,在验证集上具有约 82% 的准确度。
总结
本文介绍了图卷积如何表示为多项式,以及如何使用消息传递机制来近似它。这种具有附加特征变换的方法具有强大的表示能力。本文中仅仅触及了图卷积和图神经网络的皮毛。图卷积层和聚合函数有十几种不同的体系结构。并且在图上能够完成的任务任务也很多,如节点分类、边缘重建等。所以如果想深入挖掘,PyG教程是一个很好的开始。