【Ray Tracing】光线追踪中的相机模型

原理

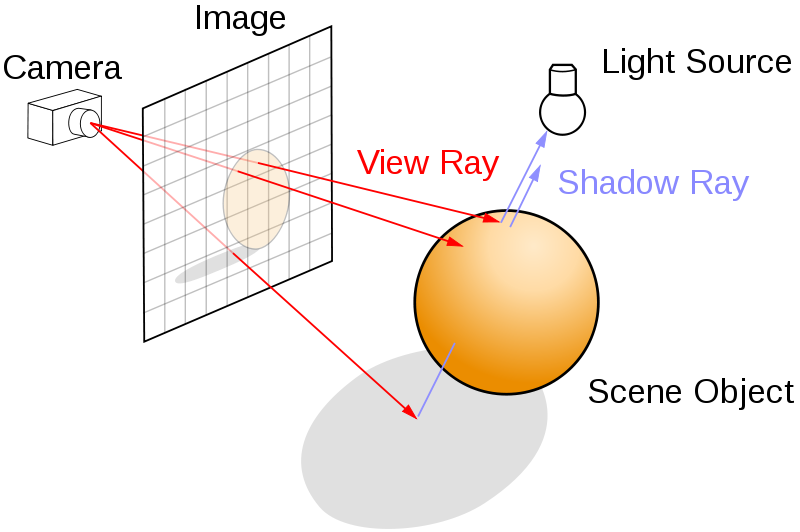
相机在光线追踪系统中，负责在图像的取样位置，生成一束光线。

相机和人眼类似，实现的是透视投影(perspective projection). 透视投影从视点(view point, eye position), 向某个方向观察场景，观察的角度范围称为视野(field of view, FOV)。 出了定义观察的前向(forward)是哪个方向之外，还需要定义在成像平面上，何谓上下和左右。

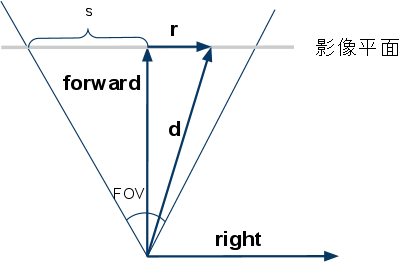
上图显示的是一个相机模型。

forward 和 right 分别是前向和右向的单位向量

由于像平面是大小可变的（分辨率不同）， 为了计算方便，我们在这里设定同一的取样坐标 (s_x,sy), 以左下角为 (0,0), 以右上角为 (1,1).

因为视点是固定的，所以光线的起点不变。要生成光线，只需要用采样坐标(s_x,sy) 计算其方向 d. d 可以分解为 right x forward x up 这三个正交单位向量上的投影

• forward 方向投影就是 单位 1
• 以上图水平左右方向为例， tan(fov/2)=s/forward, 而 forward 是单位向量，所以 s=tan(fov/2). 通过 (s_x−0.5)×2 将 s_x:(0,1)→(−1,1), 再乘以水平方向的长度s, 就是在 right 方向的投影r。
• 竖直上下方向同上。

实现

简化版， 方形成像，水平和竖直方向的 fov 相同

perspectiveCamera.h

#ifndef PERSPECTIVECAMERA_H
#define PERSPECTIVECAMERA_H
#include "cray.h"
class perspectiveCamera{
    public:
    perspectiveCamera();
    ~perspectiveCamera();
    perspectiveCamera(const GVector3& _eye,const GVector3& _front,const GVector3& _refUp,float _fov);
    CRay generateRay(float x,float y);

    private:
    GVector3 eye;
    GVector3 front;
    GVector3 refUp;
    float   fov;
    GVector3 right;
    GVector3 up;
    float   fovScale;
};
#endif

perspectiveCamera.cpp

#include"perspectiveCamera.h"

perspectiveCamera::perspectiveCamera()
{

}
perspectiveCamera::~perspectiveCamera()
{
}
perspectiveCamera::perspectiveCamera(const GVector3& _eye,const GVector3& _front,const GVector3& _refUp,float _fov)
{
    eye=_eye;
    front=_front;
    refUp=_refUp;
    fov=_fov;
    right=front.crossMul(refUp);
    up = right.crossMul(front);
    fovScale = tan(fov* (PI  * 0.5f / 180)) * 2;
}
CRay perspectiveCamera::generateRay(float x,float y)
{
    GVector3 r = right*((x - 0.5f) * fovScale);
    GVector3 u = up*((y - 0.5f) * fovScale);
    GVector3 tmp=front+r+u;
    tmp.normalize();
    return CRay(eye,tmp);
}

实践

在实际应用中，通常水平和竖直方向的 fov 是不同的，需要分别计算 fovx 和 fovy. 这和最终成像的图像分辨率是相关的。

在实际应用中，视点到成像平面的距离是焦距 f, 通常不是单位距离 1. 这时候，tan(fov/2)=s/f→s=ftan(fov/2), d 在 forward 方向的投影距离是 f，而不再是默认的单位 1。

版权声明：本文为CSDN博主「北境の守卫」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/baishuo8/article/details/81664720