作者:saltriver
当用均值滤波器降低图像噪声的时候,会带来图像模糊的副作用。我们当然希望看到的是清晰图像。那么,清晰图像和模糊图像之间的差别在哪里呢?从逻辑上考虑,图像模糊是因为图像中物体的轮廓不明显,轮廓边缘灰度变化不强烈,层次感不强造成的,那么反过来考虑,轮廓边缘灰度变化明显些,层次感强些是不是图像就更清晰些呢。
那么,这种灰度变化明显不明显怎样去定义呢。我们学过微积分,知道微分就是求函数的变化率,即导数(梯度),那么对于图像来说,可不可以用微分来表示图像灰度的变化率呢,当然是可以的,前面我们提到过,图像就是函数嘛。
在微积分中,一维函数的一阶微分的基本定义是这样的:
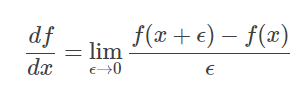
而图像是一个二维函数f(x,y),其微分当然就是偏微分。因此有:
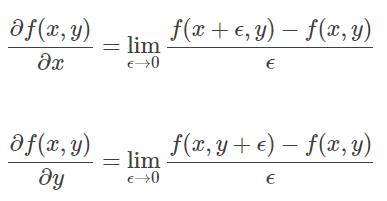
因为图像是一个离散的二维函数,ϵ 不能无限小,我们的图像是按照像素来离散的,最小的 ϵ 就是 1 像素。因此,上面的图像微分又变成了如下的形式(ϵ=1):
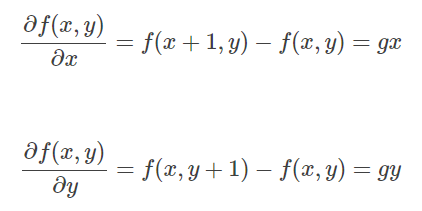
这分别是图像在(x, y)点处x方向和y方向上的梯度,从上面的表达式可以看出来,图像的梯度相当于2个相邻像素之间的差值。
那么,这个梯度(或者说灰度值的变化率)如何增强图像的清晰度呢?
我们先考虑下x方向,选取某个像素,假设其像素值是100,沿x方向的相邻像素分别是90,90,90,则根据上面的计算其x方向梯度分别是10,0,0。这里只取变化率的绝对值,表明变化的大小即可。
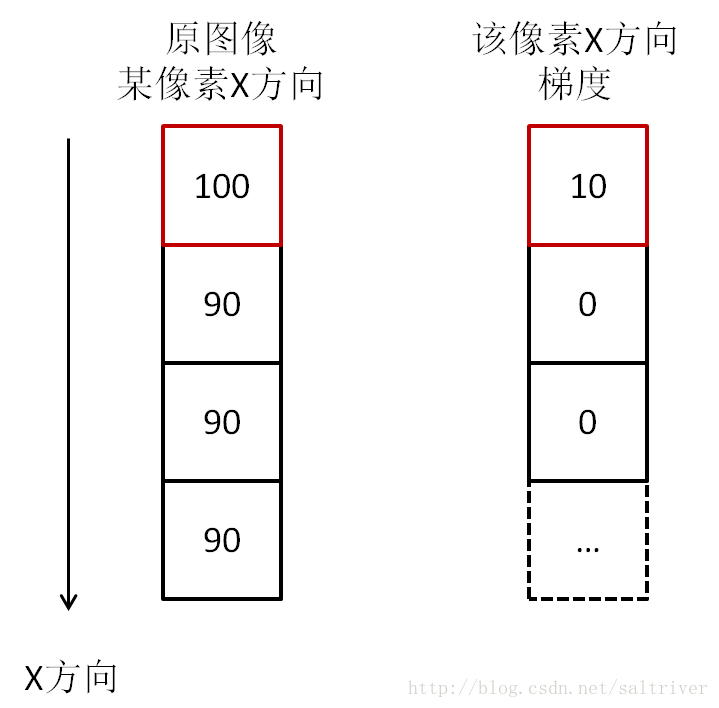
我们看到,100和90之间亮度相差10,并不是很明显,与一大群90的连续灰度值在一起,轮廓必然是模糊的。我们注意到,如果相邻像素灰度值有变化,那么梯度就有值,如果相邻像素灰度值没有变化,那么梯度就为0。如果我们把梯度值与对应的像素相加,那么灰度值没有变化的,像素值不变,而有梯度值的,灰度值变大了。
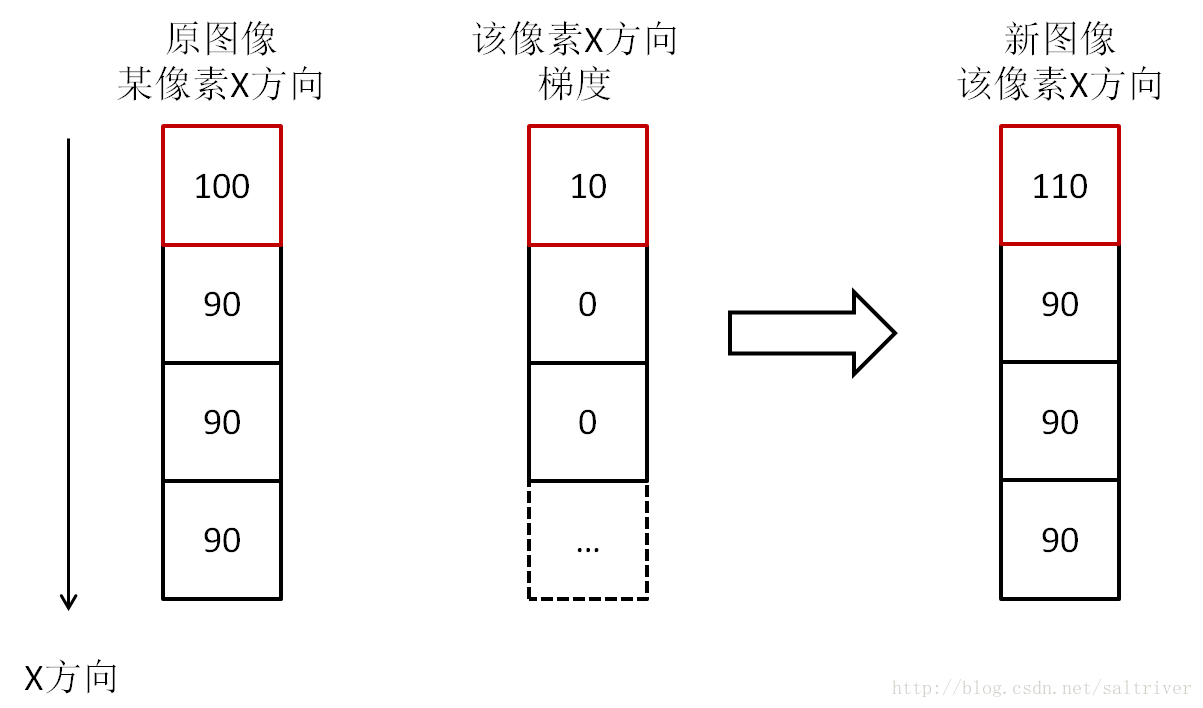
我们看到,相加后的新图像,原图像像素点100与90亮度只相差10,现在是110与90,亮度相差20了,对比度显然增强了,尤其是图像中物体的轮廓和边缘,与背景大大加强了区别,这就是用梯度来增强图像的原理。
上面只是说了x方向,y方向是一样的。那么能否将x方向和y方向的梯度结合起来呢?当然是可以的。x方向和y方向上的梯度可以用如下式子表示在一起:
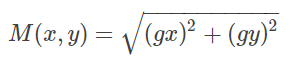
这里又是平方,又是开方的,计算量比较大,于是一般用绝对值来近似平方和平方根的操作,来降低计算量:
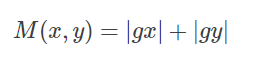
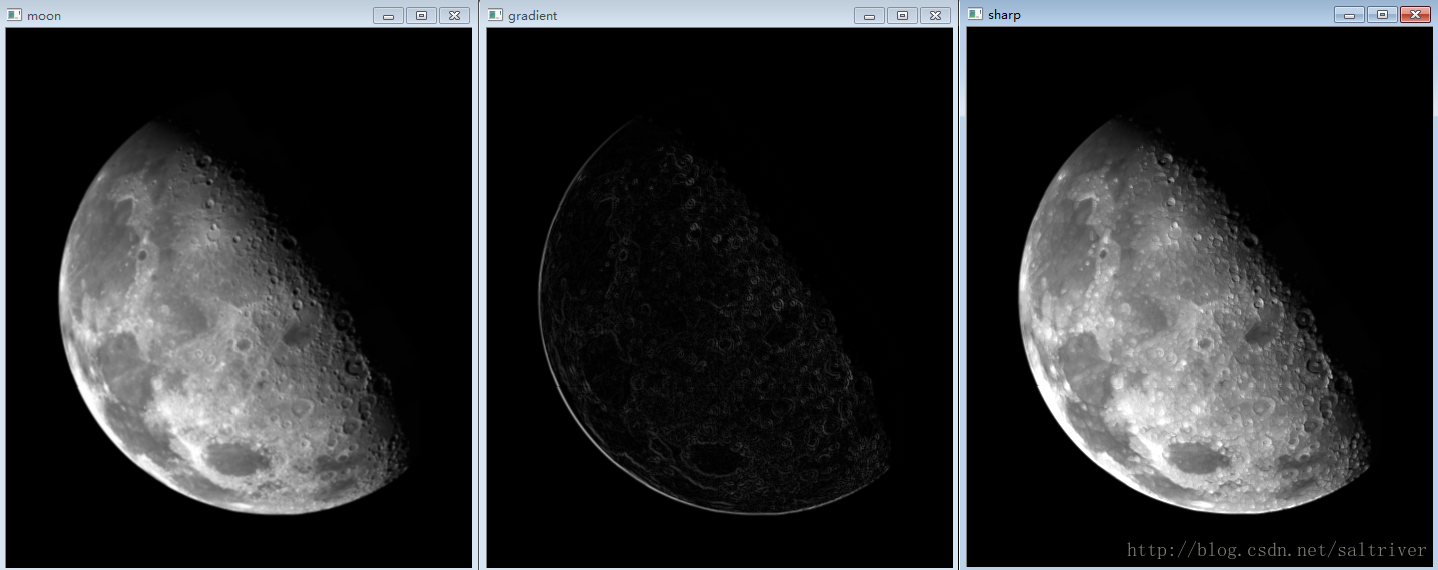
我们来计算一下月球图像的x方向和y方向结合的梯度图像,以及最后的增强图像。(原图像来自冈萨雷斯的《数字图像处理》一书。)
import cv2
import numpy as np
moon = cv2.imread("moon.tif", 0)
row, column = moon.shape
moon_f = np.copy(moon)
moon_f = moon_f.astype("float")
gradient = np.zeros((row, column))
for x in range(row - 1):
for y in range(column - 1):
gx = abs(moon_f[x + 1, y] - moon_f[x, y])
gy = abs(moon_f[x, y + 1] - moon_f[x, y])
gradient[x, y] = gx + gy
sharp = moon_f + gradient
sharp = np.where(sharp < 0, 0, np.where(sharp > 255, 255, sharp))
gradient = gradient.astype("uint8")
sharp = sharp.astype("uint8")
cv2.imshow("moon", moon)
cv2.imshow("gradient", gradient)
cv2.imshow("sharp", sharp)
cv2.waitKey()
版权声明:本文为CSDN博主「saltriver」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/saltriver/article/details/78987096



