作者:Remy Lau
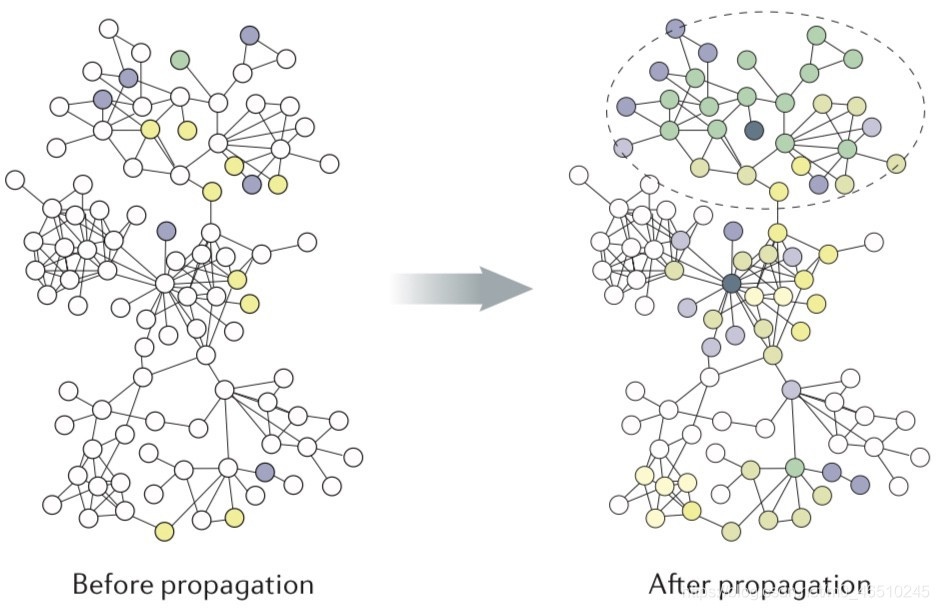
你可能听说过图卷积,因为它在当时是一个非常热门的话题。虽然不太为人所知,但网络传播是计算生物学中用于网络学习的主要方法。在这篇文章中,我们将深入研究网络传播背后的理论和直觉,我们也将看到网络传播是图卷积的一种特殊情况。
① 网络传播是计算生物学中基于内疚关联原理的一种流行方法。
② 两种不同的网络传播观点:随机游走和扩散,以HotNet2为例。
③ 网络传播是图卷积的一种特例。
计算生物学中的网络传播
网络自然产生于许多真实世界的数据,如社交网络,交通网络,生物网络,仅举几个例子。网络结构编码了关于网络中每个个体角色的丰富信息。
在计算生物学中,像蛋白质相互作用(PPI)这样的生物网络,节点是蛋白质,边缘代表两个蛋白质相互作用的可能性,在重建生物过程,甚至揭示疾病基因方面非常有用[1,2]。这种重建可以简单地通过直接观察目标蛋白的邻近蛋白是否是生物过程或疾病的一部分来完成。这种通过邻近蛋白质来推断蛋白质隶属度的过程称为网络传播。我们将在下一节中更仔细地研究精确的数学公式,但是现在让我们想想为什么这样一个简单的方法有效。
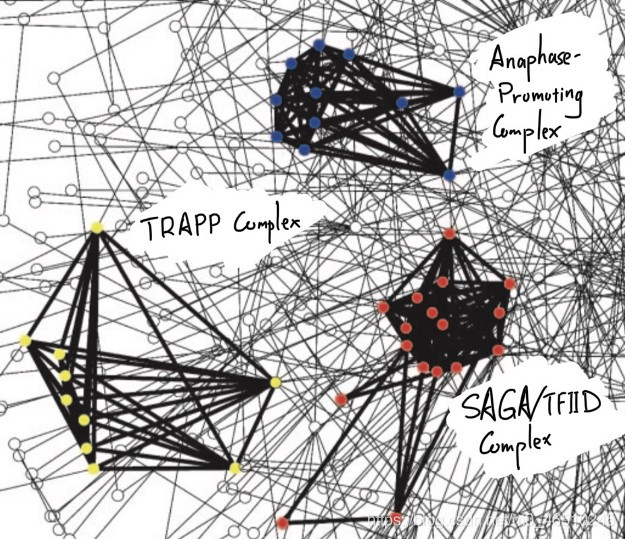
这一切都归结为内疚关联(GBA)原则,即通过物理交互作用或其他相似度量(如基因共同表达),蛋白质彼此紧密相关,可能参与相同的生物过程或途径。GBA原理来自于观察到许多蛋白质复合物(如酵母[3]中的SAGA/TFIID复合物)定位于一个内聚网络模块。同样,在人类疾病基因网络[4]中,我们可以看到,例如,与耳、鼻、喉疾病或血液病相关的疾病基因都局限在网络模块中。作为旁注,在这篇文章中,蛋白质和基因这两个词将互换使用。
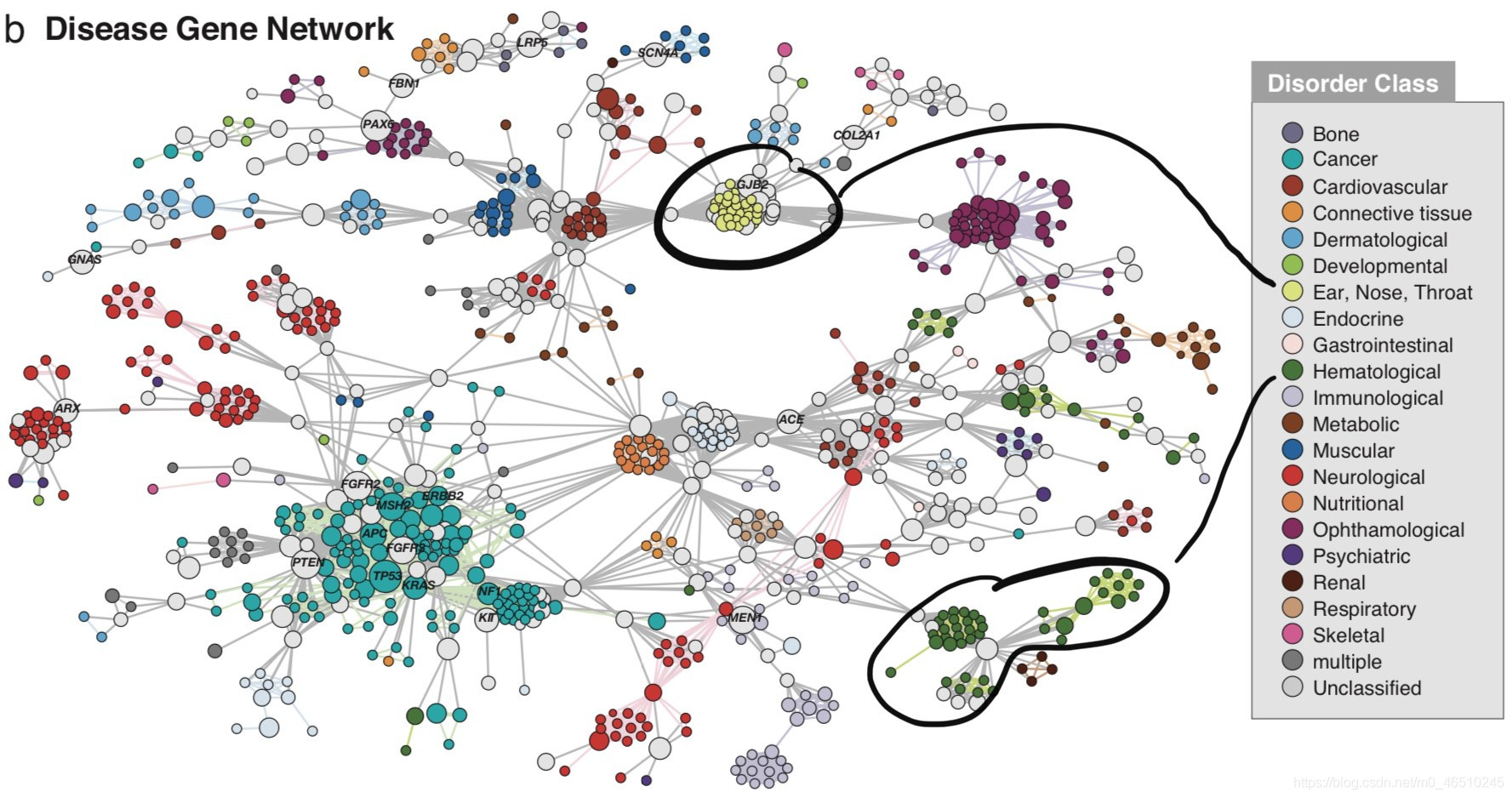
网络传播的数学公式——两种不同的观点
1. 符号
给定一个(无向)图 G = (V, E, w),有 n 个顶点的顶点集 V,边集 E,权函数 w,设 A 为相应的 n × n 维邻接矩阵:
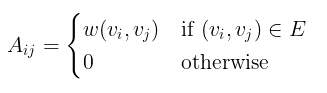
利用对角度矩阵D,它的对角项是相应节点的度,我们可以将A按行或按列规格化,得到两个新的矩阵P和W。
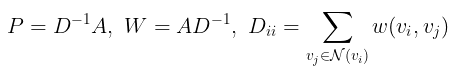
最后,设 p0 为°热编码的标签向量,其中 p0 对应的正标签节点的项为 1,其余均为 0 。
观点1:随机游走
我们可以在网络上以随机游走的方式进行网络传播。在这种情况下,我们要问的关键问题如下。
通过一跳传播,从目标节点开始并最终到达任何一个具有正标签的节点的概率是多少?
在数学上,该操作对应于P和p0之间的矩阵向量乘法,得到预测得分向量y:
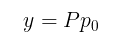
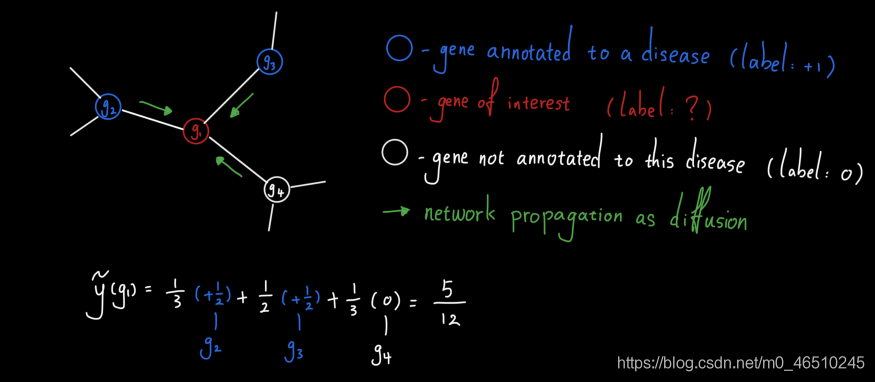
让我们看一个例子。考虑基因g1、g2、g3和g4的以下子网。假设g2和g3被注释到一种疾病中,这意味着已知这两个基因与此处研究的疾病有关。另一方面,g1和g4没有对该疾病进行注释(注意:这并不意味着它们对该疾病没有影响,而是目前还不知道它们与该疾病有关)。

为了确定g1是否与疾病相关,我们可以简单地设计一个从g1开始的单跳随机行走,看看它落在疾病基因(g2或g3)上的概率是多少。经过简单的计算,我们看到预测得分是2/3,这是相当高的。这是有道理的,因为g1的三个邻近基因中有两个与疾病相关,而根据GBA原理,g1很可能与这种疾病相关。
观点2:扩散
网络传播的另一种观点是通过网络进行扩散。在这种情况下,我们要问的关键问题如下。
有多少“热度”被扩散到目标节点?或者换句话说,从带有正标签的节点开始,通过一跳传播最终到达目标节点的概率是多少?
数学上,该操作对应于波浪号P和p0 (p0的标准化版本)之间的矩阵向量乘法,产生预测得分向量y波浪号。

注:p0 归一化保证了从一个概率分布映射到一个概率分布,即 y 波浪号等于1。
让我们回到上面的例子,通过网络传播疾病基因预测。这一次,我们想将标签传播作为扩散来执行。结果,两个注释疾病基因产生的总“热”中有很大一部分(5/12)被g1收集。因此g1很可能与本病相关。
超越了单跳传播
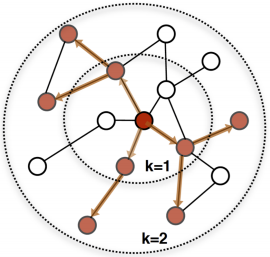
单跳传播方法简单有效。然而,当标记数据稀缺时(这是计算生物学中典型的情况),单跳传播方法只能计算疾病基因直接邻居的非平凡预测分数。考虑到人类基因组中有超过2万个基因,这显然导致了次优预测。因此,我们可以扩展到2-hop, 3-hop,甚至更多,而不是局限于1-hop社区。图中显示了k-hop从k = 1到k = 2的传播过程。
HotNet2扩散
有许多不同的变体来执行多跳扩散或随机游走。我们将以HotNet2为例。与上面介绍的扩散类似,HotNet2算法迭代更新初始“heat”分布p0波浪线如下。

其中beta值从0到1,是将“热量”带回其源头的“重启概率”。包含这个重启概率的原因有几个(有些相关)。首先,之前定义的扩散算子给出了当前节点拥有的所有“热量”,因此在第t步,之前所有的扩散信息都丢失了。添加beta有效地在每一步中保留了一些热量,因此在第t步,分布包含了之前步骤的所有信息。其次,(非零)beta参数保证了t趋近于无穷时热分布的收敛性,从而给出了t=∞时热分布的封闭形式解:
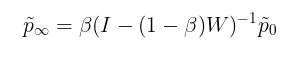
最后,在[1]中已经证明,在生物通路重建、疾病基因预测等方面,这种HotNet2扩散方法比上一节定义的单跳网络传播能够产生持续更好的预测。
与图卷积的关系
回想一下,图卷积网络遵循如下的分层传播规则:
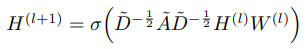
其中H(l)是第l层的隐藏特征,W(l)是可学习参数,非线性σ (DAD)内部的主导部分是具有自连接的谱归一化邻接矩阵。自连接的作用类似于重新启动概率,以保留当前迭代的一些信息。
通过下面的替换,我们可以完全重建标签传播作为图卷积的一种特殊情况。
用行归一化(P)或列归一化(W)版本替换谱归一化自连接邻接矩阵
用p(l)代替H(l)
用恒等式代替非线性和W(l)(或者干脆忽略这些变换)
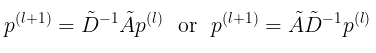
注意,第一次替换不会改变图的频谱,因此仍然会执行相同的卷积操作。
现在你知道了,网络传播是图卷积的一种特殊情况!
总结
基于关联原理,网络传播由于细胞组织的模块化,在计算生物学中被广泛应用于疾病基因预测等各种任务。我们已经深入研究了网络传播的两个观点及其与图卷积的联系。
引用
[1] R. Liu, C. A. Mancuso, A. Yannakopoulos, K. A. Johnson, A. Krishnan, Supervised learning is an accurate method for network-based gene classification (2020), Bioinformatics
[2] L. Cowen, T. Ideker, B. J. Raphael, R. Sharan, Netowork propagation: a universal amplifier of genetic associations (2017), Nat Rev Genet
[3] V. Spirin and L. A. Mirny, Protein complexes and functional modules in molecular networks (2003), Proceedings of the National Academy of Sciences
[4] K. Goh, M. E. Cusick, D. Valle, B. Childs, M. Vidal, A. Barabasi, The human disease network (2007), Proceedings of the National Academy of Sciences
[5] W. L. Hamilton, R. Ying, J. Leskovec, Inductive Representation Learning on Large Graphs (2017), arXiv
[6] T. N. Kipf and M. Welling, Semi-Supervised Classification with Graph Convolutional Networks (2016), arXiv
作者:Remy Lau
原文地址:https://towardsdatascience.com/network-learning-from-network-propagation...
本文转自:DeepHub IMBA,转载此文目的在于传递更多信息,版权归原作者所有。如不支持转载,请联系小编demi@eetrend.com删除。