清华大学计图团队首创三角网格面片上的卷积神经网络，首次取得100%正确率

来源： 图形学与几何计算

近日，清华大学计图 (Jittor) 团队提出了一种针对三角网格的卷积神经网络，在两个网格分类数据集上首次取得 100% 正确率，在其他多个几何学习任务中，性能显著超过现有方法。

尤为重要的是，这种基于细分表示的网格卷积神经网络的提出，使得 VGG、ResNet 和 DeepLabV3 + 等二维图像的骨干网络模型可以方便地应用到三维模型的学习上，从而突破了二维图像和三维模型在深度学习上的壁垒，将极大地促进三维视觉、虚拟现实、智慧城市和无人驾驶等领域的发展。

三角网格上的卷积网络

三维几何学习是计算机视觉与图形学中的一个重要研究方向，基于三维体素、点云、网格（mesh）等数据表示，学习物体的几何形状特征。其中，网格广泛应用于建模、渲染、3D 打印等。因为网格数据较为复杂，包含点、边、面三种基本元素，缺乏规则的结构与层次化的表示，因此也更具挑战。

近日，清华大学 Jittor 团队在 arXiv 发布了论文《Subdivision-Based Mesh Convolution Networks》，提出了一种基于细分结构的网格卷积网络 SubdivNet。该方法首先将输入网格进行重网格化（remesh），构造细分结构，得到一般网格的多分辨率表示，并提出了直观灵活的面片卷积方法、上 / 下采样方法，并将成熟的图像网络架构迁移到三维几何学习中。

论文链接：https://arxiv.org/abs/2106.02285

图 1 SubdivNet 的流程图

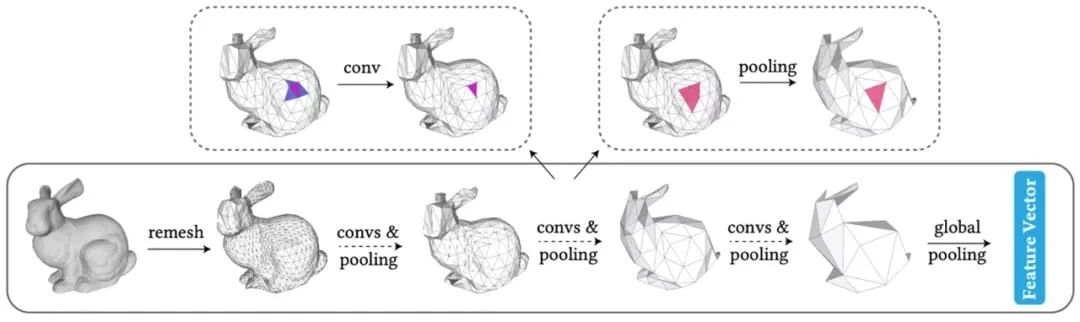
面片卷积与上下采样

以往的网格深度学习方法将特征存储在点或者边上，但是点的度数不固定，边的卷积不灵活。该论文提出了一种在面片上的网格卷积方法，充分利用了每个面片与三个面片相邻的规则性质。基于这一规则性质，Jittor 团队进一步依据面片之间的距离，设计了多种不同的卷积模式。

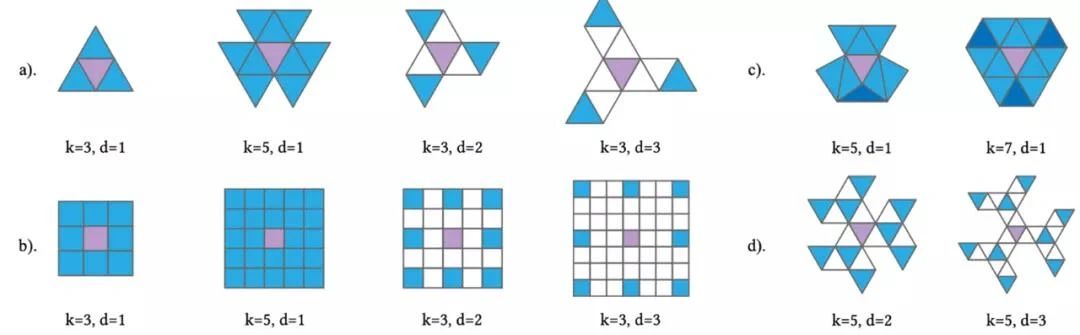
从图 2 可以看到，这种面片上的网格卷积方法，直观且灵活，有规律，可支持指定卷积核大小、步长、空洞等参数，很类似于图像的情形。图中，k 为卷积核大小，d 为空洞长度；
其中
a)为三角面片卷积，
b)对应的二维图像卷积，
c)为卷积中可能出现的重复访问，
d)为更复杂的卷积示例。

图 2 三角网格上的卷积示意图

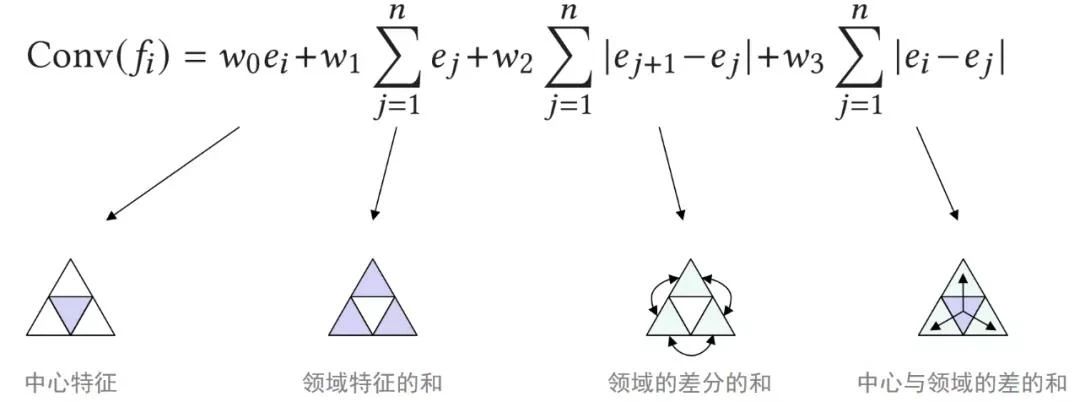
由于三维数据格式中的面片顺序不固定，SubdivNet 在计算卷积结果时，通过取邻域均值、差分均值等方式，使得计算结果与面片顺序无关，满足排列不变性。图 3 给出了卷积的定义及其每项的含义。

图 3 卷积的定义及其每项的含义

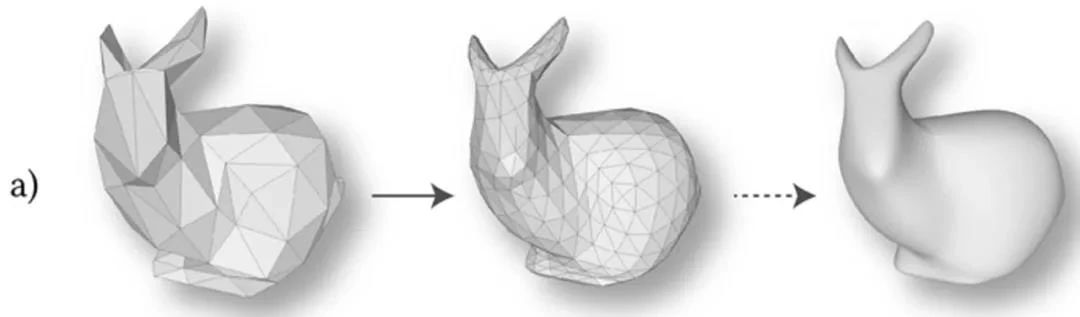
在进行上下采样时，该方法受到传统的 Loop 细分曲面建模的启发，构造了一种基于细分结构的上下采样方法。如图 4a）所示，细分曲面建模对面片进行 「一分四」 的面片分裂，使得三维模型逐渐变得光滑。

该论文首先将网格进行重网格化，使其面片具有细分连接结构，从而可以进行 「四合一」的面片合并，从高分辨率转为低分辨率，实现面片特征的 pooling 操作，如图 4b）所示。上采样时，同样对面片进行 「一分四」的分裂。这样定义上下采样方式是规则且均匀的，还可以实现双线性插值等需求。

图 4 细分曲面的示意图

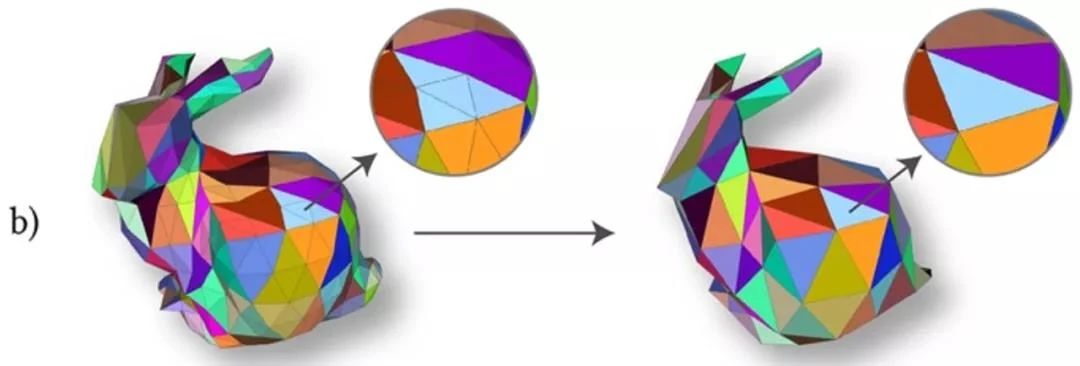
由于卷积和上下采样规则且灵活，Jittor 团队实现了 VGG、ResNet 和 DeepLabV3 + 等网络架构，在三维网格模型的实验中取得了显著的效果。

该工作由清华大学的深度学习框架 Jittor 实现，Jittor 框架提供了高效的重索引算子，无需额外的 C++ 代码即可实现邻域索引；并且在同等网格面片数量下，SubdivNet 的速度可达以往方法 [2] 的 20 多倍。

GitHub 开源地址为：https://github.com/lzhengning/SubdivNet

实验结果

SubdivNet 在多种应用方面进行了实验，展示了其在几何学习上的优势。更多的消融实验可以阅读原论文。

1. 网格分类

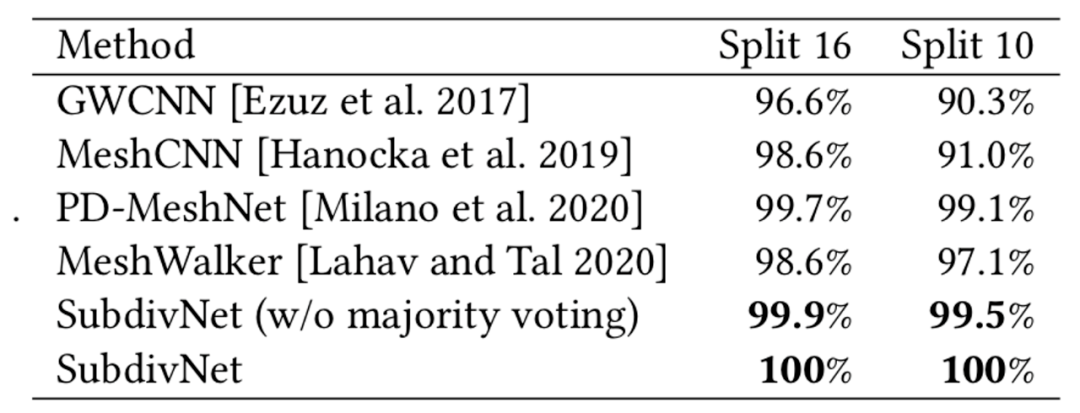
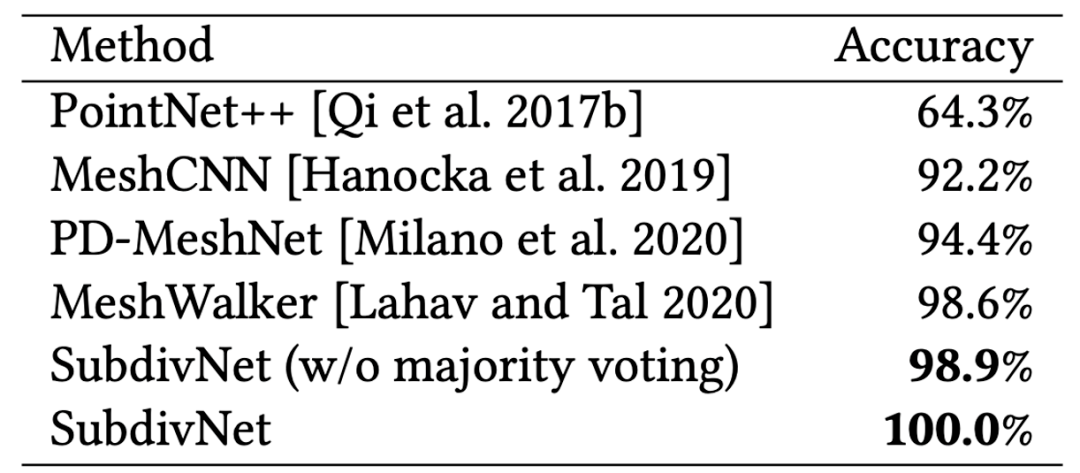
SubdivNet 在三个网格分类数据集中进行了实验比较，如表 1 和表 2 所示。其中，在 SHREC11 和 Cube Engraving 两个数据集上首次达到了 100% 的分类正确率。

表 1 在 SHREC11 数据集上的分类精度
表 2 在 CubeEngraving 数据集上的分类精度

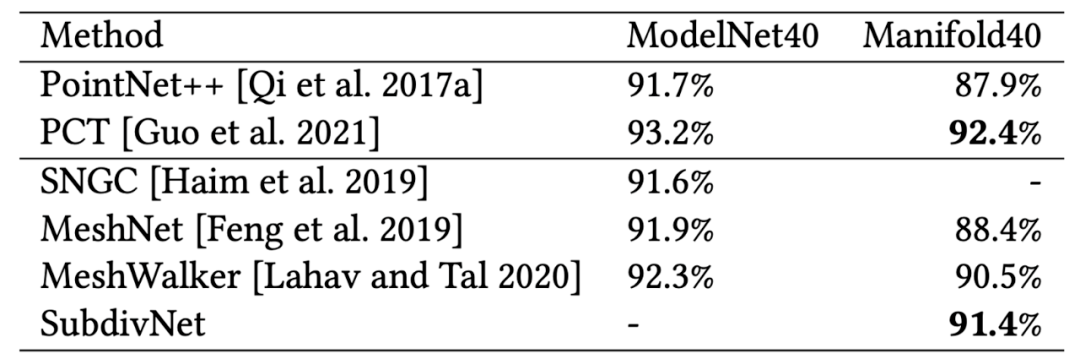
该方法还把 ModelNet40 中的模型修复为紧致流形，贡献了新的数据集 Manifold40 。在此数据集上，SubdivNet 也超过了以往的网格方法。表 3 给出 ModelNet40 和 Manifold40 上的分类精度，其中前两行以位置和法向为输入的点云的最好结果，后三行是网格模型的结果。

表 3 在 Manifold40 数据集上的分类精度

2. 网格分割

计图团队在人体分割数据集、COSEG 数据集上进行了网格分割的实验。量化指标下，SubdivNet 的分割准确率均高于对比的点云、网格方法。以下是分割结果展示。

图 5 人体分割结果
图 6 COSEG 玩具分割结果

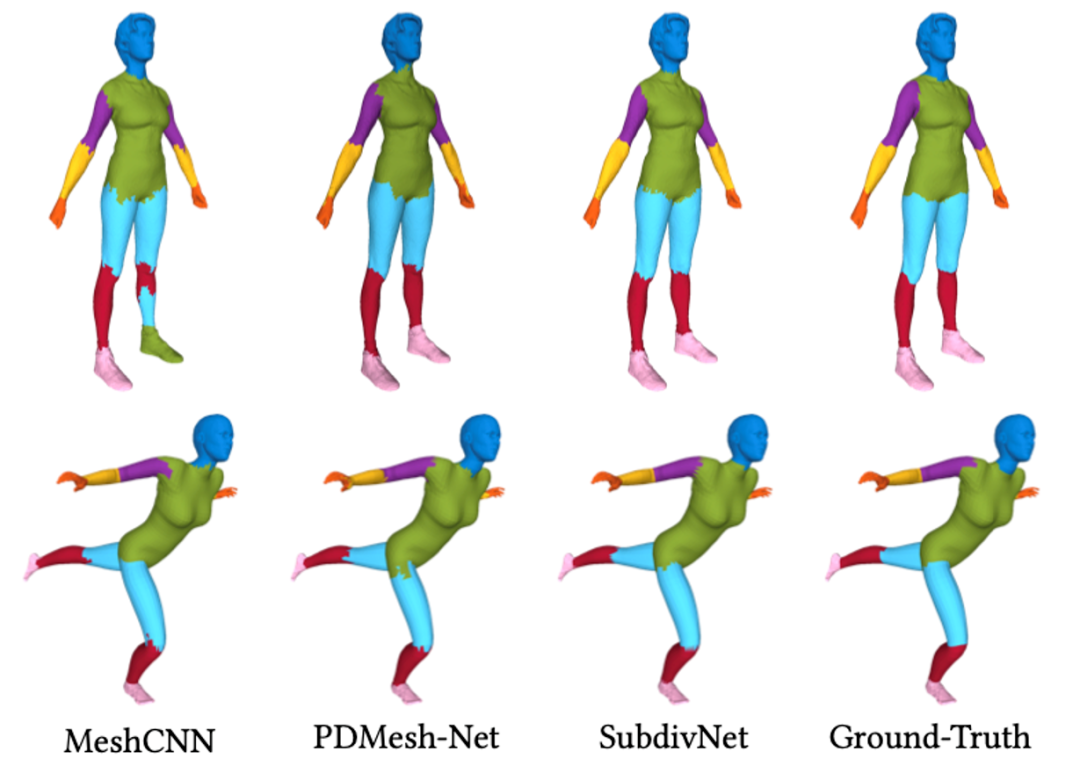
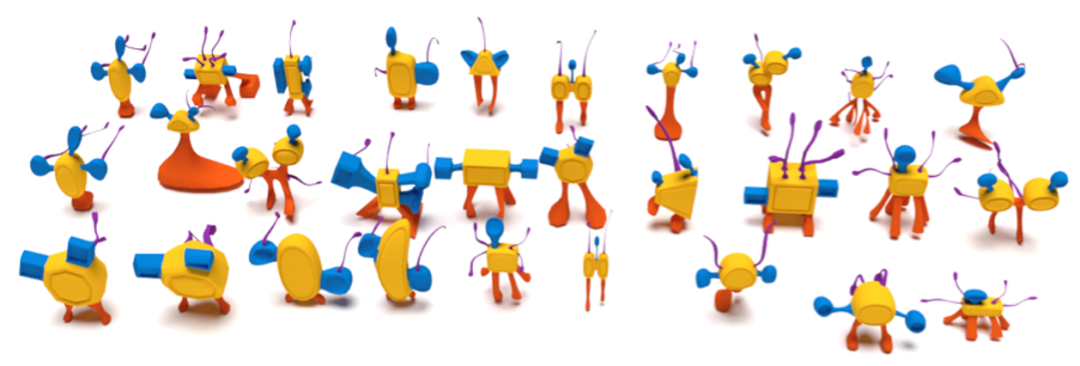
3. 形状对应

在量化的形状对应实验中，SubdivNet 达到了 SOTA性能。图 6 中，给定 Source Mesh 的点，寻找 Target Mesh 中与之对应点；相同的颜色表示对应关系。

图 7 形状对应可视化结果

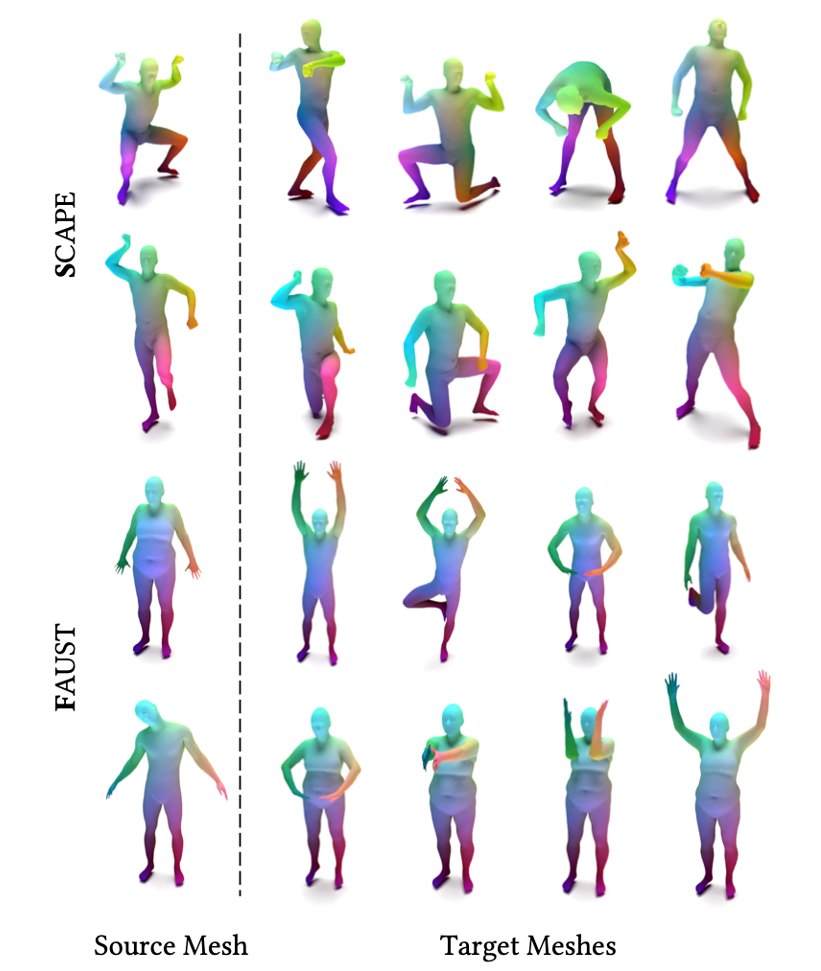
4. 网格检索

Jittor 团队还利用 RGBD 相机扫描了真实场景，以点云为输入，在网格数据库中检索相似网格模型；以下为一些检索结果。

图 8 从真实场景检索数据库中的三位网格模型

参考文献
Shi-Min Hu, Zheng-Ning Liu, Meng-Hao Guo, Jun-Xiong Cai, Jiahui Huang, Tai-Jiang Mu, Ralph R. Martin， Subdivision-Based Mesh Convolution Networks, 2021, arXiv:2106.02285.
Rana Hanocka, Amir Hertz, Noa Fish, Raja Giryes, Shachar Fleishman, Daniel Cohen-Or, Meshcnn: a network with an edge, ACM Transactions on Graphics, Vol. 38 No. 4, Article No. 90, 1-12.