本文主要介绍锯齿产生的原因,几种简单的抗锯齿技术,像前置滤波,后置滤波,基于光线追踪的抗锯齿技术中的一种。这篇文章是为后面介绍分布式射线追踪(Distributed Ray Tracing),随机采样(Stochastic Sampling)和累积缓存(Accumulation Buffer)作铺垫。
一. 锯齿的介绍
锯齿的概念最早出现在信号采样的采样理论中,以一定频率离散的采样一个信号,如果采样频率不够大就会发生锯齿。如图(1)所示的两个sine波,圆圈表示采样点。对(a)图中的sine波以图中所示的采样频率采样,足以构造出原始的sine波;对(b)图中的sine波以同样的采样频率采样,构造出来的sin波的频率就会降低,这就是一个锯齿信号(Aliased Signal)。奈奎斯特定理(Nyquist Theorem)就指出,为了精确的重构原始的信号,采样频率必需是原始信号中最高频率的两倍。在给定采样频率的条件下,能精确重构的信号中的最大频率是奈奎斯特极限(Nyquist Limit),即对所有在极限范围内的信号以给定的采样频率采样,可以精确的重构出原始信号,对超过那个范围的信号就会发生锯齿,出现下图的情况了。

在图形学范畴中,像素是一个个离散的点,在显示器上的光栅显示就相当于对图像进行采样,对于给定分辨率的显示器相当于给定了采样频率。如果要显示的图像的最高频率超过了奈奎斯特极限,就会发生锯齿,在图形学中称之为jaggies,翻译成中文也是锯齿的意思。
最好的避免锯齿的方法是要有足够大的采样频率,例如针对图形学来说,就是要有足够大的分辨率。但在多数情况下,并不能满足这个条件,所以就需要采用一些其它技术来解决这个问题。
显示器清晰度不够,能产生锯齿,使用一些高清显示器就可以解决这个问题,但这里叙述几种在显示器清晰度不够的情况下解决锯齿问题的技术,处理锯齿问题的方法称为抗锯齿技术。
二. 抗锯齿技术

图2(a)显示了图片未使用抗锯齿技术时发生失真,越靠近图片顶部,棋盘格子越小,图片越难以辨识;而图2(b)采用了一种抗锯齿操作,靠近顶部的棋盘逐渐变在灰色,在屏幕分辨率不足以显示远处的格子时,这种效果更加可接受,而越近的格子也越光滑;图(c)使用了另外一种抗锯齿算法,是基于sinc过滤器的抗锯齿算法,能达到比图片(b)更好的效果。
还有一些抗锯齿技术,像将图像模糊(bluring),根据Nyquist采样理论,是给定采样频率,通过降低原始信号的频率来使得信号能够被重构出来,如图3所示。对模糊化处理和未处理的原图像进行下采样,得到图中底部的两张图,模糊化处理的原图像下采样的图像还能看出一些轮廓,而未处理的原图像下采样的图像就显得更加混乱。

从上面看出,采用抗锯齿技术,可以一定程度上缓解样本不足导致的失真。这里在图形学的角度,介绍三种抗锯齿技术。
2.1. 前置滤波(Prefiltering)
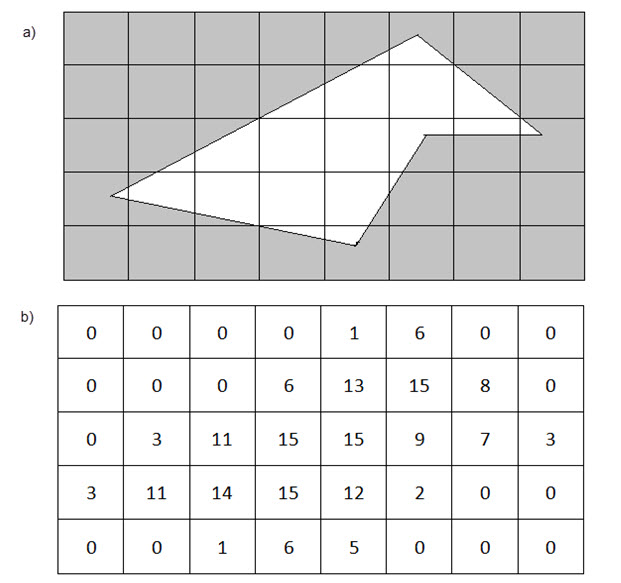
前置滤波技术,是通过物体的覆盖范围来计算其像素颜色值的,即一个像素的多少区域被物体覆盖。每个像素会有一个灰度(Intensity),该值依赖物体或者直线对像素所在区域的覆盖率,如图4所示。灰度是0,表示黑色;灰度是1,表示白色。如果一个像素的一半被多边形覆盖,灰度是1/2;如果1/3被覆盖,灰度是1/3,依次类推。如果帧缓冲区中每个像素占4位,则黑色用0表示,白色用15表示,所以每个像素值是像素灰度值乘以15,图4(a)中的多边形,可以用图4(b)中的像素值来表示。
找到每个像素的灰度需要较大的运算量,这里介绍一种方法是由Pitteway和Watkinson提出的,是对布雷森汉姆直线绘制算法(参见文章《布雷森汉姆直线算法》)进行的修改。基本思想是:多边形填充时,采用的是逐行扫描的方式,用AEL数据结构确定要填充的像素段,当一条扫描线被填充完成后,采用布雷森汉姆算法更新存储在AEL结点中的数据xint,即改变了文章《区域填充算法和多边形填充的扫描线算法》2.2中所叙述的原则2。
通过一个例子来说明该算法,图5中的边的斜率是m=4/10,像素值所在方格用标准的布雷森汉姆算法进行计算,方格中像素强度依次为0.5,0.9,0.3,初始像素值是0.5。从左到右扫描边,如果y方向的坐标值不变,则像素强度加上m=0.4,如果y方向的坐标值加1,则像素的灰度值减去1-m=0.6,这相比于《区域填充算法和多边形填充的扫描线算法》中的多边形填充算法,锯齿问题能得到一定程度的缓解。

最后演示一个由参考【5】中找到的两张前置滤波的例子,如图6所示。总结下:前置滤波必需考虑对象的几何细节并计算每个像素的平均灰度,对于处理除多边形形状以外的几何图元来说,前置滤波运算量非常的大,不太适用。

2.2. 后置滤波(Postfiltering)
首先介绍一个很重要的概念,就是超采样(Supersample),简单来说,就是原先一个像素只选择一个采样样本,现在一个像素中选取多个采样样本,即以亚像素(subpixel)作为样本。如图7所示,一个格子表示一个像素,每个像素上取9个采样点,即水平分辨率和垂直分辨率都是原来的3倍。如果要绘制圆圈A中的像素,因为有6个采样点在圆圈内部,3个采样点在外部,所以计算得到它的颜色值为:(2/3*圆圈内颜色+1/3圆圈外颜色)。B像素的9个采样点颜色都一样,它的颜色值就多边形的颜色,即圆圈内的颜色。
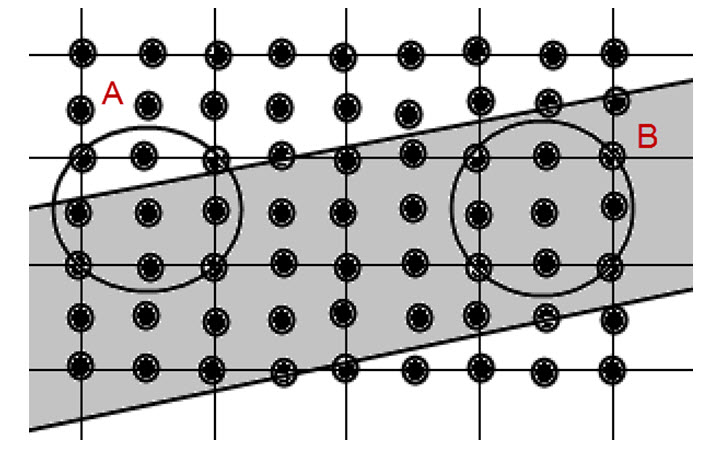
超采样或者后置滤波是通过提高采样样本的频率,然后再将结果取平均,从而得到一个抗锯齿的图片效果。
基本的过程是:
(1)通过超采样得到的高分辨率的虚拟图像,它的分辨率比帧缓冲区中存储的的帧的分辨率高;
(2)将高分辨率的虚拟图像降低分辨率,这就称为后置滤波,因为滤波是在采样完成后进行的。
对得到的高空间分辨率的虚拟图像降低分辨率的方法有多种,可以采用将颜色值乘以对应的比例系数的方法,也可以采用与周围的几个像素进行加权计算的方法。如图8所示,当窗口函数应用到右下角的一个像素时,计算得到30/2+(28+16+4+42+30+17+53+60+62)/16 = 32.625,就是该像素的像素值。窗口模板可以是3*3,或者4*4等等,不同的窗口模板尺寸和数值,能产生不同的实验效果。

参考【6】中,作者实验了几种不同的窗口模板,并对比得到的实验结果,在参考【7】的空间滤波基础一小节中,提供了各种不同的模板的应用,这里不详细讨论各种窗口模板。最后,演示从网上找到的一个实验结果,参考【8】。



2.3. 基于光线追踪的抗锯齿(Ray Tracing)
基于光线追踪的抗锯齿技术还有很多,这里只介绍了其中的一种。
在参考【9】的论文中,作者基于光线追踪的理论,提出了一种发光模型,并将光线追踪的理论应用到抗锯齿的操作上,简单介绍下该抗锯齿技术。采样过疏可以导致锯齿发生,由计算机生成的图像中发生锯齿包括下面几种情况:
(1)在一个平面的轮廓发生突变的区域;
(2)很小的物体落在采样点和非采样点之间时;
(3)应用映射到平面上的采样函数(比如纹理函数)。
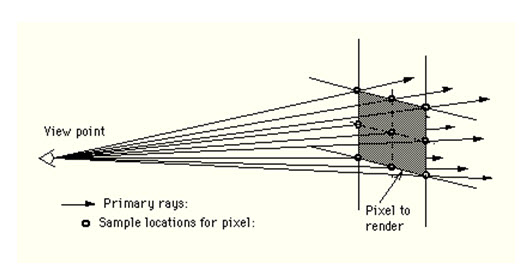
该算法的思想是:每个像素可以用一个方格来表示,一条由眼睛起始的光线射向像素方格的四个角,计算这四个角的平均强度(Intensity,这里我觉得还是翻译成强度的好)。将该平均值分别与四个角的值进行比较,对于差别过大的角将继续进行细分,依次类推下去,算法的思想与Warnock的HSR算法类似。
三. 参考
【1】Paper,Robert L. Cook,“Stochastic Sampling in Computer Graphics”
【2】http://en.wikipedia.org/wiki/Spatial_anti-aliasing
【3】http://en.wikipedia.org/wiki/Sinc_filter
【4】http://redwood.berkeley.edu/bruno/npb261/aliasing.pdf
【5】http://web.cs.wpi.edu/~matt/courses/cs563/talks/antialiasing/methods.html
【6】Paper,Franklin C. Crow,“A Comparision of Antialiasing Techniques”
【7】冈萨雷斯《数字图像处理》第二版,第3.5节空间滤波基础
【8】http://web.cs.wpi.edu/~matt/courses/cs563/talks/antialiasing/supersampli...
【9】Paper,Turner Whitted…”An Improved Illumination Model for Shaded Display”
【10】http://web.cs.wpi.edu/~matt/courses/cs563/talks/antialiasing/adaptive.html
【11】《Computer Graphics using OpenGL, Second Edition》
来源
作者:TwinklingStar
原文链接:http://www.twinklingstar.cn/2013/390/introduction-to-alias-antialias/
转载此文目的在于传递更多信息,版权归原作者所有。






