1、引言
在深度学习中,神经网络模型是其较为常见的模型之一。神经网络已经在计算机视觉、自然语言处理、语音识别等领域取得了突飞猛进的发展,其强大的特征学习能力引起了国内外学者的广泛关注,有着十分广泛的应用前景。但是,神经网络在训练样本中表现得过于优越,导致在验证数据集以及测试数据集中表现不佳,这种情况称为过拟合。过拟合常常在模型学习能力过强的情况中出现,此时的模型学习能力太强,以至于将训练集单个样本自身的特点都能捕捉到,并将其认为是“一般规律”,从而导致模型泛化能力下降。
2、 过拟合产生原因
假设我们要拟合一群二次函数分布的数据,使用神经网络对这些数据进行拟合。图1显示了训练模型达到最佳模型,为二次多项式。
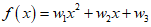
图2显示了训练中为了拟合更多的点,而使训练模型变得更加复杂,模型的泛化能力变弱,为六次多项式。
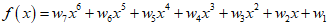
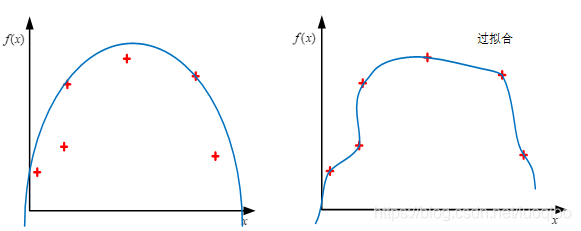
从上面的例子中我们总结出过拟合现象产生的原因如下:
① 建模样本选取有误,如样本数量太少,如果有足够的样本分布在二次项曲线两侧,则过拟合程度将减弱[4]。
② 参数太多,模型复杂度过高。
③ 训练时间过长,没有在拟合程度恰当时停止训练。
针对过拟合现象产生的原因,整理了当前神经网络减少过拟合常用的四种方法:Early Stopping、和正则化、Dropout与数据增强,并进行详细的探讨。
3 过拟合的解决方案
3.1 Early Stopping
为了获得性能良好的神经网络,网络定型过程中需要进行许多关于所用设置超参数的决策[7]。超参数之一是定型周期(epoch)的数量:亦即应当完整遍历数据集epoch多少次呢?如果epoch数量太少,网络有可能发生欠拟合;如果epoch数量太多,则有可能发生过拟合。
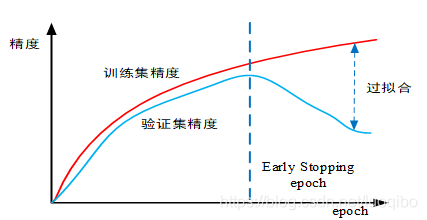
我们可以将数据分为训练集和验证集,每个epoch结束后(或每N个epoch后),在验证集上获取测试结果,随着epoch的增加,如果在验证集精度上发现测试精度下降,则停止训练。将停止之后的epoch超参数作为网络的最终参数。其精度与epoch的关系如图3所示。
这种Early Stopping的方案并没有采取解决损失函数和降低方差的问题,仅仅使训练模型不因为训练批次epoch的增加而降低。
3.2 和正则化
为了避免正则化,一个非常常用的方法是正则化(regularization)。正则化的思想就是损失函数中加入刻画模型复杂程度的指标。假设用于刻画在训练数据上表现的损失函数为loss(θ),那么在优化时不是直接优化loss(θ),而是优化loss(θ)+λR(w)。其中R(w)刻画的是模型复杂程度,而λ表示模型复杂损失在总损失中的比例。这里的θ表示的是神经网络中所有的参数,包括边上的权重w和偏置项b。一般来说模型复杂程度只有权重w决定。常用刻画模型复杂程度的函数R(w)有两种,一种是正则化,计算公式是:
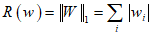
另一种是正则化,计算公式是:

无论是那种正则化方式,基本思想都是希望通过限制权重的大小,使模型不能任意拟合数据中的随机噪音。但是这两种正则化的方法也有很大的区别,首先,正则化会让参数变得稀疏,而正则化不会。所谓参数变得稀疏是指会让更多的参数变为0,这样就可以达到类似特征选取的功能。之所以正则化不会让参数变得稀疏的原因是当参数很小时,比如0.001,这个参数的平方基本上就可以忽略了,于是模型不会进一步将这些参数调整为0。在实践中,也可以将正则化与正则化同时使用:
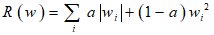
3.3 Dropout
Dropout是由辛顿等人提出的一种提高网络范化能力的方法。所谓Dropout,是指在网络训练过程中,按照一定的概率将部分中间层的元暂时从网络中丢弃,通过把该单元的输出设置为0使其不工作,来避免过拟合。Dropout可以用于训练包含全连接层的神经网络。神经网络的训练过程就是对每个batch使用误差反向传播算法不断迭代调整各参数的值,而Dropout就是在每次迭代调整的过程中,随机选取一部分神经元使其输出值设置为0(如图4)。
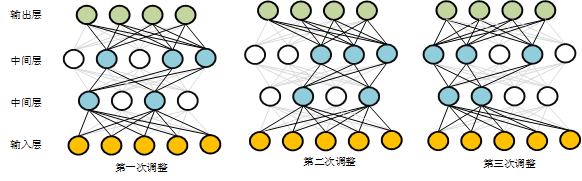
自Dropout被提出以来,人们已经通过各种基准测试证明了其有效性,它已经成为深度学习中不可或缺的一种技术。训练时网络通过Dropout舍弃了一定概率的单元,但是在识别时仍要使用所有单元。由于单元止之间通过权重系数相连接,所以我们这里还是要乘以Dropout的概率。像这样的网络进行参数约束后仍然能训练出合理的网络,这就达到了抑制过拟合的目的。
3.4 数据增强
一般而言,比较成功的神经网络需要大量的参数,而使得这些参数可以正确工作则需要大量的数据进行训练,而实际情况中数据并没有我们想象中的那么多。但是我们可以利用已有的数据比如翻转(如图5)、缩放(如图6)等,创造出更多的数据,来使得神经网络具有更好的泛化效果。


版权声明:本文为CSDN博主(luoqibo)原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/luoqibo/article/details/102711804






