一、降维技术主要分为两大类:特征选择和特征提取。
基本概念:特征选择:我们可以选出原始特征的一个子集。特征提取:通过现有信息进行推演,构造出一个新的特征子空间。
为什么要降维:
(1)数据的多重共线性导致解的空间不稳定, 维度灾难,模型复杂,导致模型的泛化能力弱;
(2)高维空间样本具有稀疏性,导致模型比较难找到数据特征;
(3)过多的变量会妨碍模型查找规律;
(4)有时特征矩阵过大, 导致计算量比较大,训练时间长的问题。
降维的目的:
(1)减少特征属性的个数,剔除不相关或冗余特征,减少特征个数,提高模型精确度,减少运行时间。
(2)确保特征属性之间是相互独立的
1、特征选择
sklearn.feature_selection :模块中的类可以用来对样本集进行 feature selection(特征选择)和 dimensionality reduction(降维),这将会提高学习器的准确度或者增强它们在高维数据集上的性能。
特征选择的功能:减少特征数量、降维,使模型泛化能力更强,减少过拟合;增强对特征和特征值之间的理解。
下面是sklearn中的几种常见的特征选择方法:
各个方法的使用链接:https://scikit-learn.org/stable/modules/feature_selection.html#univariat...
中文链接:https://sklearn.apachecn.org/#/docs/14?id=_113-%E7%89%B9%E5%BE%81%E9%80%...
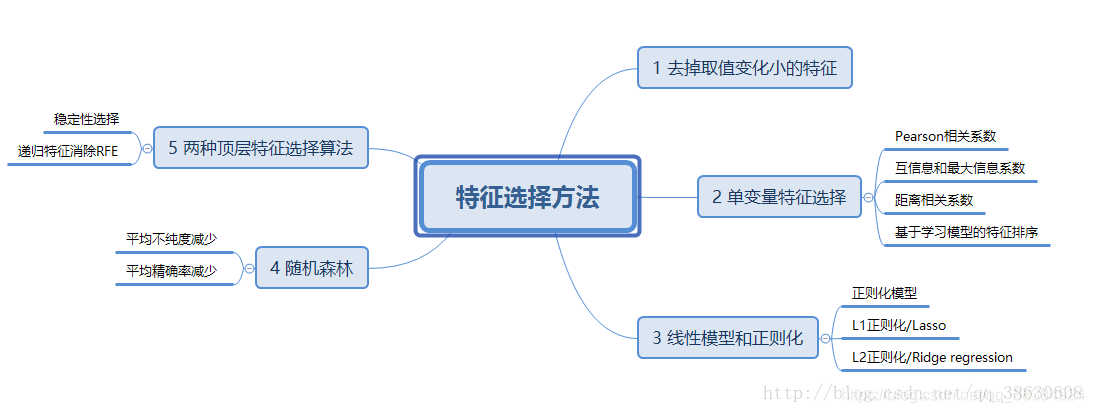
1.1、去掉取值变化小的特征:(Removing features with low variance),
此方法只有在特征为离散型变量时才使用,如果是连续则要离散化。某特征的特征值只有0和1,若95%的样本在该特征的取值都为1,那么该特征就没什么意义,也就是变化比较小。但实际中,很少有这样的特征,一般将它作为特征选择的预处理,然后再用其他方法进行选择。
VarianceThreshold:是特征选择中的一项基本方法。它会移除所有方差不满足阈值的特征。默认设置下,它将移除所有方差为0的特征,即那些在所有样本中数值完全相同的特征。
1.2、单变量特征选择:(Univariate feature selection) ,
通过基于单变量的统计测试来选择最好的特征。它可以当做是评估器的预处理步骤。衡量它们与响应变量之间的关系,根据得分扔掉不好的特征。如:在回归和分类中,可以使用卡方检验等方式对也特征进行测试。这种方法有许多改进的版本、变种。
(1)、Pearson相关系数 Pearson Correlation:能帮助理解特征和响应变量之间关系衡量的是变量之间的线性相关性,结果的取值区间为[-1,1],-1表示完全的负相关(这个变量下降,那个就会上升),+1表示完全的正相关,0表示没有线性相关。作为特征排序机制时,只对线性关系敏感。Scipy的 pearsonr 方法能够同时计算相关系数和p-value。
(2)、互信息和最大信息系数 (Mutual information and maximal information coefficient (MIC) ):互信息系数:能够很好地度量各种相关性,计算复杂,不过很多toolkit都包含此工具(例如sklearn的MINE),得到相关性就可以排序选择特征了。最大信息系数寻找一种最优的离散化方式,然后把互信息取值转换成一种度量方式,取值区间在[0,1],通常变量要先离散化。
(3)、距离相关系数 (Distance correlation):Pearson相关系数是0,我们也不能断定这两个变量是独立的(有可能是非线性相关);但如果距离相关系数是0,那么我们就可以说这两个变量是独立的。
(4)、基于学习模型的特征排序 (Model based ranking):构建单个特征的模型,通过模型的准确性为特征排序,借此选择特征。当选择到了目标特征之后,再用来训练最终的模型。
思路:先选择机器学习算法,再针对每个单独的特征和响应变量建立预测模型。
某个特征和响应变量之间的关系是:
(1)线性的:其实Pearson相关系数等价于线性回归里的标准化回归系数。
(2)非线性的:可以用基于树的方法(决策树、随机森林)、或者扩展的线性模型等。
基于树的方法比较易于使用,因为他们对非线性关系的建模比较好,并且不需要太多的调试。但要注意过拟合问题,因此树的深度最好不要太大,再就是运用交叉验证。
注意:该基于学习模型,是针对单独特征和响应变量之间的模型,下面的就是基于机器学习模型的方法1.3,1.4。
1.3、线性模型和正则化:
1.2中的单变量特征选择方法独立的衡量每个特征与响应变量之间的关系,另一种主流的特征选择方法是基于机器学习模型的方法。有些机器学习方法本身就具有对特征进行打分的机制,或者很容易将其运用到特征选择任务中,例如回归模型,SVM,决策树,随机森林等等。
(1)线性模型:用回归模型的系数w来选择特征。越是重要的特征在模型中对应的系数就会越大,而跟输出变量越是无关的特征对应的系数就会越接近于0。在噪音不多的数据上,或者是数据量远远大于特征数的数据上,如果特征之间相对来说是比较独立的,那么即便是运用最简单的线性回归模型也一样能取得非常好的效果。逻辑回归同理。
(2)正则化模型:正则化就是把额外的约束或者惩罚项加到已有模型(损失函数)上,以防止过拟合并提高泛化能力。损失函数由原来的E(X,Y)变为E(X,Y)+alpha||w||,w是模型系数组成的向量,||·||一般是L1或者L2范数,alpha是一个可调的参数,控制着正则化的强度。当用在线性模型上时,已有损失函数后加L1正则化称为Lasso、已有损失函数后加L2正则化称为Ridge regression、已有损失函数后加L1正则化和L2正则化称为Elastic Net。
(2.1)、L1正则化/Lasso:L1正则化将系数w的l1范数作为惩罚项加到损失函数上,由于正则项非零,这就迫使那些弱的特征所对应的系数变成0。因此L1正则化往往会使学到的模型很稀疏(系数w经常为0),L1正则方法具有稀疏解的特性,因此天然具备特征选择的特性,稀疏解他们的许多系数为 0。 当目标是降低使用另一个分类器的数据集的维度, 它们可以与feature_selection.SelectFromModel 一起使用来选择非零系数。
(2.2)L2正则化/Ridge regression:L2正则化对于特征选择来说一种稳定的模型,不像L1正则化那样,系数会因为细微的数据变化而波动。所以L2正则化和L1正则化提供的价值是不同的,L1没有选到的特征不代表不重要,原因是连个具有高相关性的特征可能只保留了一个,如果要确定哪个特征重要应再通过L2正则方法交叉检验。
(2.3)ElasticNet :是一种使用L1和L2先验作为正则化矩阵的线性回归模型.这种组合用于只有很少的权重非零的稀疏模型,比如:Lasso, 但是又能保持Ridge 的正则化属性。当多个特征和另一个特征相关的时候弹性网络非常有用。Lasso 倾向于随机选择其中一个,而弹性网络更倾向于选择两个,具体来说,应该分别使用L1和L2拟合,如果两个特征在L2中系数相接近,在L1中一个系数为0一个系数不为0,那么其实这两个特征都应该保留,原因是L1对于强相关特征只会保留一个。
1.4、 随机森林
随机森林具有准确率高、鲁棒性好、易于使用等优点,这使得它成为了目前最流行的机器学习算法之一。随机森林提供了两种特征选择的方法:mean decrease impurity和mean decrease accuracy。可以用sklearn中在训练了RandomForestClassifier后,通过feature_importances来得到这些内容。根据重要程度给不同特征赋予不同的重要等级。无须做标准化或归一化处理。还可以设定阈值的基础上进行特征选择。
(1)平均不纯度减少 mean decrease impurity
随机森林由多个决策树构成。决策树中的每一个节点都是关于某个特征的条件,为的是将数据集按照不同的响应变量一分为二。利用不纯度可以确定节点(最优条件),对于分类问题,通常采用 基尼不纯度 或者 信息增益 ,对于回归问题,通常采用的是 方差 或者最小二乘拟合。当训练决策树的时候,可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说,可以算出每个特征平均减少了多少不纯度,并把它平均减少的不纯度作为特征选择的值。
(2)平均精确率减少 Mean decrease accuracy
另一种常用的特征选择方法就是直接度量每个特征对模型精确率的影响。主要思路是打乱每个特征的特征值顺序,并且度量顺序变动对模型的精确率的影响。很明显,对于不重要的变量来说,打乱顺序对模型的精确率影响不会太大,但是对于重要的变量来说,打乱顺序就会降低模型的精确率。
1.5、两种顶层特征选择算法
之所以叫做顶层,是因为他们都是建立在基于模型的特征选择方法基础之上的,例如回归和SVM,在不同的子集上建立模型,然后汇总最终确定特征得分。
(1) 稳定性选择 Stability selection
稳定性选择是一种基于二次抽样和选择算法相结合较新的方法,选择算法可以是回归、SVM或其他类似的方法。它的主要思想是在不同的数据子集和特征子集上运行特征选择算法,不断的重复,最终汇总特征选择结果,比如可以统计某个特征被认为是重要特征的频率(被选为重要特征的次数除以它所在的子集被测试的次数)。理想情况下,重要特征的得分会接近100%。稍微弱一点的特征得分会是非0的数,而最无用的特征得分将会接近于0。sklearn在 随机lasso 和 随机逻辑回归 中有对稳定性选择的实现。
(2)递归特征消除 Recursive feature elimination (RFE)
递归特征消除的主要思想是反复的构建模型(如SVM或者回归模型)然后选出最好的(或者最差的)的特征(可以根据系数来选),把选出来的特征放到一边,然后在剩余的特征上重复这个过程,直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序。因此,这是一种寻找最优特征子集的贪心算法。RFE的稳定性很大程度上取决于在迭代的时候底层用哪种模型。例如,假如RFE采用的普通的回归,没有经过正则化的回归是不稳定的,那么RFE就是不稳定的;假如采用的是Ridge,而用Ridge正则化的回归是稳定的,那么RFE就是稳定的。Sklearn提供了 RFE 包,可以用于特征消除,还提供了 RFECV ,可以通过交叉验证来对的特征进行排序。
1.6、总结
(1)对于理解数据、数据的结构、特点来说,单变量特征选择是个非常好的选择。尽管可以用它对特征进行排序来优化模型,但由于它不能发现冗余(例如假如一个特征子集,其中的特征之间具有很强的关联,那么从中选择最优的特征时就很难考虑到冗余的问题)。
(2)正则化的线性模型对于特征理解和特征选择来说是非常强大的工具。L1正则化能够生成稀疏的模型,对于选择特征子集来说非常有用;相比起L1正则化,L2正则化的表现更加稳定,由于有用的特征往往对应系数非零,因此L2正则化对于数据的理解来说很合适。由于响应变量和特征之间往往是非线性关系,可以采用basis expansion的方式将特征转换到一个更加合适的空间当中,在此基础上再考虑运用简单的线性模型。
(3)随机森林是一种非常流行的特征选择方法,它易于使用,一般不需要feature engineering、调参等繁琐的步骤,并且很多工具包都提供了平均不纯度下降方法。它的两个主要问题,1是重要的特征有可能得分很低(关联特征问题),2是这种方法对特征变量类别多的特征越有利(偏向问题)。尽管如此,这种方法仍然非常值得在你的应用中试一试。
(4)特征选择在很多机器学习和数据挖掘场景中都是非常有用的。在使用的时候要弄清楚自己的目标是什么,然后找到哪种方法适用于自己的任务。当选择最优特征以提升模型性能的时候,可以采用交叉验证的方法来验证某种方法是否比其他方法要好。当用特征选择的方法来理解数据的时候要留心,特征选择模型的稳定性非常重要,稳定性差的模型很容易就会导致错误的结论。对数据进行二次采样然后在子集上运行特征选择算法能够有所帮助,如果在各个子集上的结果是一致的,那就可以说在这个数据集上得出来的结论是可信的,可以用这种特征选择模型的结果来理解数据。
1.7、Tips
什么是卡方检验?用方差来衡量某个观测频率和理论频率之间差异性的方法
什么是皮尔森卡方检验?这是一种最常用的卡方检验方法,它有两个用途:
① 计算某个变量对某种分布的拟合程度,
② 根据两个观测变量的Contingency table来计算这两个变量是否是独立的。
主要有三个步骤:第一步用方差和的方式来计算观测频率和理论频率之间卡方值;第二步算出卡方检验的自由度(行数-1乘以列数-1);第三步比较卡方值和对应自由度的卡方分布,判断显著性。
什么是p-value?简单地说,p-value就是为了验证假设和实际之间一致性的统计学意义的值,即假设检验。有些地方叫右尾概率,根据卡方值和自由度可以算出一个固定的p-value,
什么是响应变量(response value)?简单地说,模型的输入叫做explanatroy variables,模型的输出叫做response variables,其实就是要验证该特征对结果造成了什么样的影响
2、特征提取:
前面讲了特征选择,下面讲一下特征抽取来降维,可理解为:尽可能多的保持相关信息的情况下,对数据进行压缩的一种方法。三种:都可以将原始数据集变换为一个维度更低的新的特征子集。
(1)PCA:无监督数据降维技术—主成分分析principal component analysis;
sklearn.decomposition.PCA。
主成分分析是一种用于连续属性的数据降维方法,它构造了原始数据的一个正交变换,新空间的基地去除了原始空间基底下数据的相关性,只需要使用少数新变量就能够解释原始数据中大部分变量。在应用中通常是选出比原始变量个数少,能够解释大部分数据中的变量的几个新变量,即所谓的主成分,来代替原始变量进行建模。通过线性变化,将原始数据集变化为一组各维度线性无关的表示!
在高维数据中找到最大方差的方向,将数据映射到一个不大于原始数据的新的子空间上。构建一个dXk维的转换矩阵W,来完成维度的转换。第一主成分的方差应该最大,由于各主成分之间不相关(正交),后续主成分也具备尽可能大的方差。注意:要先进行标准化处理。sklearn的decomposition类的PCA方法。参数为主成分数目。提供了PCA类,在转换前要使用训练数据对模型进行拟合。步骤:数据标准化,构造样本协方差矩阵,获得协方差矩阵的特征值和特征向量,按降序排列特征值所对应的特征向量,选择k个最大特征值对应的特征向量,其中k为新特征空间的维度,构建映射矩阵,进行转换。
(2)LDA: 基于类别可分最大化的有监督降维技术—线性判别分析linear discriminant analysis
sklearn.discriminant_analysis.LinearDiscriminantAnalysis
用来发现最优化分类的特征子空间。是有监督算法。更适用于分类的特征提取技术。步骤:标准化处理,计算均值向量,构造类间和类内的散布矩阵,计算某矩阵的特征值和特征向量,选取k个特征对应的特征向量,构造转换矩阵,映射。sklearn的lda中有LDA方法。
(3)核PCA:通过核主成分分析进行线性降维,kernel principal component analysis
sklearn.decomposition.KernelPCA
现实世界,面对非线性问题,我们使用它。将非线性可分的数据转换到一个适合对其进行线性分类的新的低维子空间上。sklearn中的decomposition模块有核PCA类,通过kernel参数选择不同的核函数。
版权声明:本文为CSDN博主(望百川归海)原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/qq_38384924/article/details/98389144






