作者:Divyanshu Mishra
编译:ronghuaiyang
导读
权值衰减和L2正则化,到底是不是同一个东西,这篇文章给你答案。
神经网络是伟大的函数逼近器和特征提取器,但有时它们的权值变得过于特定化,导致过拟合。这就是正则化概念出现的地方,我们将讨论两种主要权重正则化技术之间的细微差别,它们经常被错误地认为是相同的。
介绍
1943年,Warren McCulloch和Walter Pitts首先提出了神经网络,但当时还不够流行,因为神经网络需要大量数据和计算能力,这在当时是不可行的。但随着上述约束条件和其他训练技术的进步(如参数初始化和更好的激活函数)变得可行,它们再次开始主导各种比赛,并在各种人类辅助技术中找到了它的应用。
如今,神经网络构成了许多著名应用的最主要的部分,如自动驾驶汽车、谷歌翻译、人脸识别系统等,并应用于几乎所有人类发展所使用的技术。
神经网络非常擅长于将函数近似为线性或非线性,在从输入数据中提取特征时也非常出色。这种能力使他们在大量的任务中表现出色,无论是计算机视觉领域还是语言建模。但我们都听过这句名言:
“能力越大,责任越大。”
这句话也适用于全能的神经网络。它们作为强大的函数近似器的能力有时会导致它们通过逼近一个函数来过拟合数据集,这个函数在它被训练过的数据上表现得非常好,但在测试它之前从未见过的数据时却败得很惨。更有技术意义的是,神经网络学习的权值对给定的数据更加专门化,而不能学习可以一般化的特征。为了解决过拟合的问题,应用了一类称为正则化的技术来降低模型的复杂性和约束权值,迫使神经网络学习可泛化的特征。
正则化
正则化可以定义为我们为了减少泛化误差而不是减少训练误差而对训练算法所做的任何改变。有许多正规化策略。有的对模型添加额外的约束,如对参数值添加约束,有的对目标函数添加额外的项,可以认为是对参数值添加间接或软约束。如果我们仔细使用这些技术,这可以改善测试集的性能。在深度学习的环境中,大多数正则化技术都基于正则化估计器。当正则化一个估计量时,有一个折衷,我们必须选择一个增加偏差和减少方差的模型。一个有效的正规化是使一个有利可图的交易,显著减少方差,而不过度增加偏差。
在实践中使用的主要正规化技术有:
① L2正则化
② L1正则化
③ 数据增强
④ Dropout
⑤ Early Stopping
在这篇文章中,我们主要关注L2正则化,并讨论我们是否可以将L2正则化和权重衰减作为同一枚硬币的两面。
L2 正则化
L2正则化属于正则化技术的一类,称为参数范数惩罚。之所以提到这类技术,是因为在这类技术中,特定参数的范数(主要是权重)被添加到被优化的目标函数中。在L2范数中,在网络的损失函数中加入一个额外的项,通常称为正则化项。例如:
交叉熵损失函数的定义如下所示。
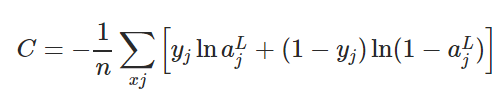
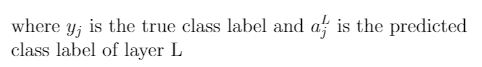
为了将L2正则化应用于任何有交叉熵损失的网络,我们将正则化项添加到损失函数中,其中正则化项如下所示:
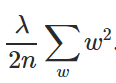
在上式中,λ是正则化参数,与应用的正则化量成正比。如果λ=0,则不应用正则化,当λ= 1时,对网络应用最大正则化。λ是一个超参数,这意味着它不是在训练期间学习的,而是由用户手动调整或使用一些超参数调整技术,如随机搜索。
现在让我们把这些放在一起,形成L2正则化的最终方程,应用于下式所给出的交叉熵损失函数。
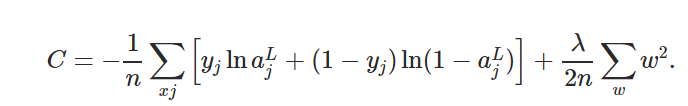
上面的例子展示了L2正则化应用于交叉熵损失函数,但这一概念可以推广到所有可用的损失函数。下式给出了L2正则化更一般的公式,其中C0为非正则化损失函数,C为加入正则化项的正则化损失函数。
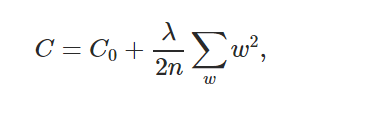
注:我们在对网络进行正则化时不考虑网络的bias,原因如下:
1、与权重相比,bias通常需要更少的数据来精确拟合。每个权重指定了两个变量如何相互作用(w和x),因此要想很好地拟合权重,就需要在各种条件下观察两个变量,而每个bias只控制一个单一变量(b)。因此,我们对bias不使用正则化,以免引入太多的方差。2、对bias进行正则化可能引入大量的欠拟合。
为什么L2 正则化有用?
实践推理:
让我们试着理解L2正则化基于损失函数的梯度的工作原理。如果我们对网络中所有权重和偏差取上面式子中所示方程的偏导数或梯度,即∂C/∂w和∂C/∂b。求偏导数,我们得到:

我们可以使用backpropagation算法计算上述方程中提到的∂C0/∂w和∂C0/∂b项。由于没有应用正则化项,偏置参数的偏导将不变,而权重参数将包含额外的(λ/n)*w)正则化项。
偏置和权重的学习规则由此变为:
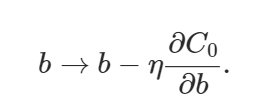
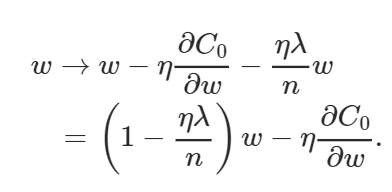
上面的权值方程类似于通常的梯度下降学习规则,除了现在我们首先通过 (1−(η*λ)/n)重新调整权值w。这就是L2正则化经常被称为权重衰减的原因,因为它使权重变小。因此,你可以看到为什么正则化工作的时候,它使网络的权值更小。权值变小意味着,如果我们在这里或那里改变一些随机输入,网络的行为不会有太大的变化,这反过来使正则化的网络很难学习数据中的局部噪声。这迫使网络只学习那些在训练集中经常看到的特征。
个人的直觉:
简单地从优化损失函数的角度来考虑L2正则化,当我们把正则化项添加到损失函数中我们实际上增加了损失函数的值。因此,如果权值越大,损失也就越高,训练算法会试图通过惩罚权值来降低损失函数,迫使它们取更小的值,从而使网络正则化。
L2 正则化和权值衰减是一样的吗?
L2正则化和权值衰减并不是一回事,但是可以根据学习率对权值衰减因子进行重新参数化,从而使SGD等价。不明白?让我给你详细解释一下。
以λ为衰减因子,给出了权值衰减方程。
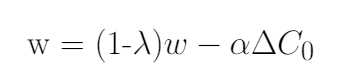
在以下证明中可以证明L2正则化等价于SGD情况下的权值衰减:
1、让我们首先考虑下面图中给出的L2正则化方程。我们的目标是对它进行重新参数化,使其等价于上式中给出的权值衰减方程。
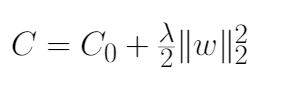
2、首先,我们找到L2正则化损失函数相对于参数w的偏导数(梯度),如下式所示。
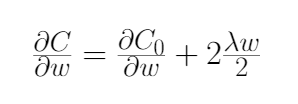
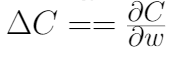
注意:上图中这两种符号的意思是一样的。
3、得到损失函数的偏导数结果后,将结果代入梯度下降学习规则中,如下式所示。代入后,打开括号,重新排列,使其等价于在一定假设下的权值衰减方程。
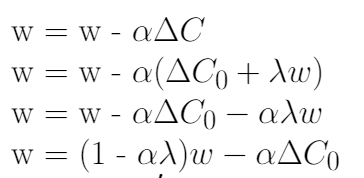
4、你可以注意到,最终重新排列的L2正则化方程和权值衰减方程之间的唯一区别是α(学习率)乘以λ(正则化项)。为了得到两个方程,我们用λ来重新参数化L2正则化方程。
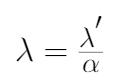
5、将λ'替换为λ,对L2正则化方程进行重新参数化,将其等价于权值衰减方程,如下式所示。
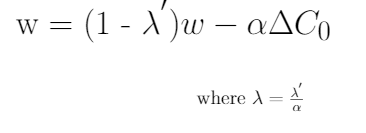
从上面的证明中,你必须理解为什么L2正则化在SGD情况下被认为等同于权值衰减,但对于其他基于自适应梯度的优化算法,如Adam, AdaGrad等,却不是这样。特别是,当与自适应梯度相结合时,L2正则化导致具有较大历史参数和/或梯度振幅的权值比使用权值衰减时正则化得更少。这导致与SGD相比,当使用L2正则化时adam表现不佳。另一方面,权值衰减在SGD和Adam身上表现得一样好。
一个令人震惊的结果是,带有动量的SGD优于像Adam这样的自适应梯度方法,因为常见的深度学习库实现了L2正则化,而不是原始的权重衰减。因此,在使用L2正则化有利于SGD的任务上,Adam的结果要比使用动量的SGD差。
总结
因此,我们得出结论,尽管权值衰减和L2正则化在某些条件下可以达到等价,但概念上还是有细微的不同,应该区别对待,否则可能导致无法解释的性能下降或其他实际问题。
英文原文:https://towardsdatascience.com/weight-decay-l2-regularization-90a9e17713cd
本文转自:AI公园,作者:Divyanshu Mishra,编译:ronghuaiyang,
转载此文目的在于传递更多信息,版权归原作者所有。






