1、为什么需要Normalization
深度学习网络模型训练困难的原因是,cnn包含很多隐含层,每层参数都会随着训练而改变优化,所以隐层的输入分布总会变化,每个隐层都会面临covariate shift的问题。
internal covariate shift(ICS)使得每层输入不再是独立同分布。这就造成,上一层数据需要适应新的输入分布,数据输入激活函数时,会落入饱和区,使得学习效率过低,甚至梯度消失。
2、Normalization的基本思想
由于cnn层数多,ICS会使激活输入分布偏移,落入饱和区,导致反向传播时出现梯度消失,这是训练收敛越来越慢的本质原因。而BN就是通过归一化手段,将每层输入强行拉回均值0方差为1的标准正态分布,这样使得激活输入值分布在非线性函数梯度敏感区域,从而避免梯度消失问题,大大加快训练速度。
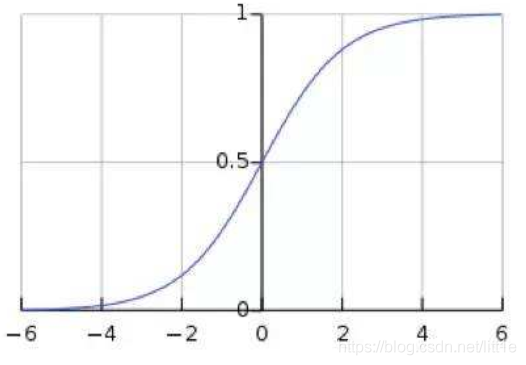
如上图,sigmoid函数,BN使输入值分布在-1~1之间,在此区间梯度值大,有效避免梯度消失并提高收敛速度。
但是,归一化后,激活输入值均被分布于-1~1之间,这会导致非线性程度降低,夸张一点说,其实输入域的分布把原来的非线性函数转变成了线性函数。这意味着网络的表达能力下降了。因此BN为了保证非线性,对变换后的满足均值为0方差为1的x又进行了scale shift操作,即y=scale*x+shift。这两个参数通过训练获得,其实又将输入分布在标准正态分布的基础上进行了平移。其实就是为了在线性与非线性间找到平衡,让泛化能力与收敛能力最大程度的体现。
3、BN中均值、方差通过哪些维度计算得到?
神经网络中传递的张量数据,其维度通常记为[N, H, W, C],其中N是batch_size,H、W是行、列,C是通道数。那么上式中BN的输入集合就是下图中蓝色的部分。
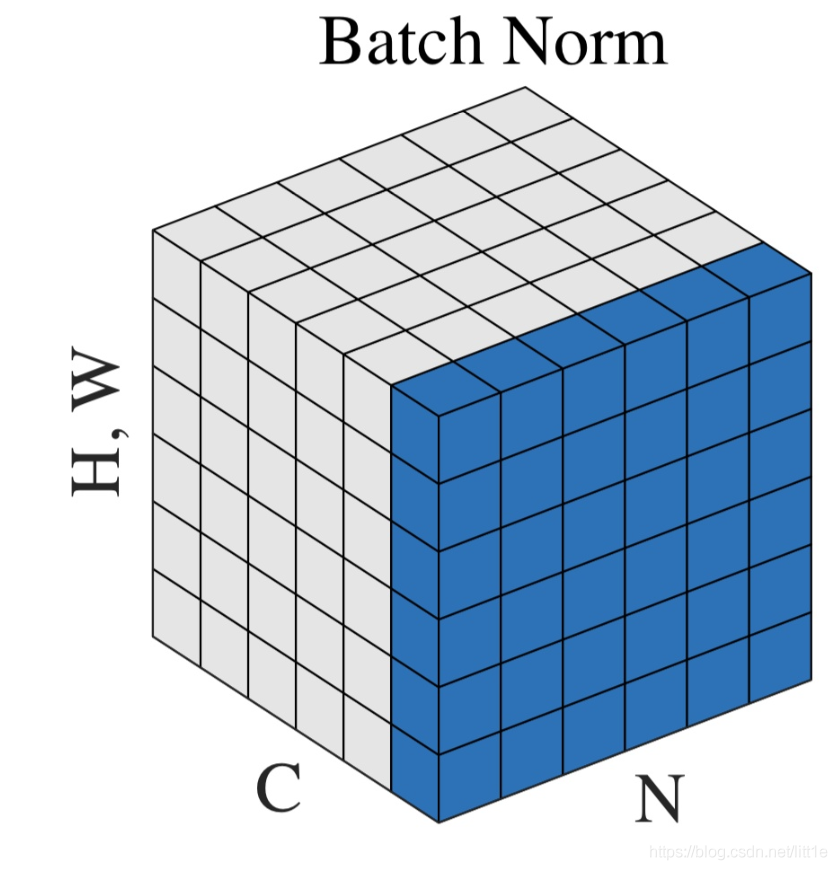
均值的计算,就是在一个批次内,将每个通道中的数字单独加起来,再除以 N×W×H。举个例子:该批次内有10张图片,每张图片有三个通道RBG,每张图片的高、宽是H、W,那么均值就是计算10张图片R通道的像素数值总和除以 10×W×H,再计算B通道全部像素值总和除以10×W×H,最后计算G通道的像素值总和除以10×W×H。方差的计算类似。可训练参数γ , β 的维度等于张量的通道数,在上述例子中,RBG三个通道分别需要一个γ 和一个 β ,所以 γ , β 的维度等于3。
4、训练BatchNorm

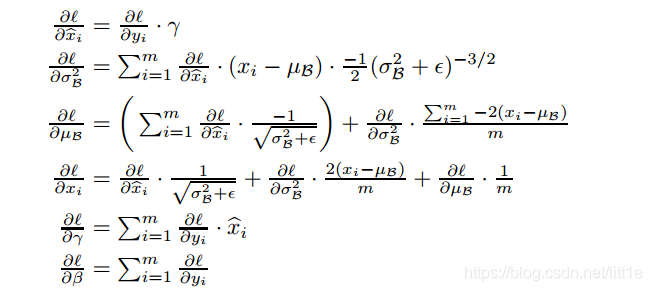
每层BN参数是根据特征图的channel数来确定的。
5、BatchNorm推理(Inference)
推理时,均值、方差是基于所有批次的期望计算所得,公式如下:
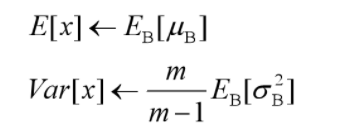
有了均值和方差,每个隐层神经元也已经有对应训练好的Scaling参数和Shift参数,就可以在推导的时候对每个神经元的激活数据计算NB进行变换了,在推理过程中进行BN采取如下方式:
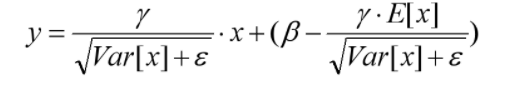
beta、gamma在训练状态下,是可训练参数,在推理状态下,直接加载训练好的数值。moving_mean、moving_var在训练、推理中都是不可训练参数,只根据滑动平均计算公式更新数值,不会随着网络的训练BP而改变数值;在推理时,直接加载储存计算好的滑动平均之后的数值,作为推理时的均值和方差。
滑动平均,储存固定个数Batch的均值和方差,不断迭代更新推理时需要的E(x),Var(x)。
6、BatchNorm的作用
1. 加快收敛速度,有效避免梯度消失。
2. 提升模型泛化能力,BN的缩放因子可以有效的识别对网络贡献不大的神经元,经过激活函数后可以自动削弱或消除一些神经元。另外,由于归一化,很少发生数据分布不同导致的参数变动过大问题。
最后还想谈一谈Instance normalization
BN适用于判别模型中,比如图片分类模型。因为BN注重对每个batch进行归一化,从而保证数据分布的一致性,而判别模型的结果正是取决于数据整体分布。但是BN对batchsize的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batchsize太小,则计算的均值、方差不足以代表整个数据分布;
IN适用于生成模型中,比如图片风格迁移,GAN等。因为图片生成的结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,在风格迁移中使用Instance Normalization不仅可以加速模型收敛,并且可以保持每个图像实例之间的独立。
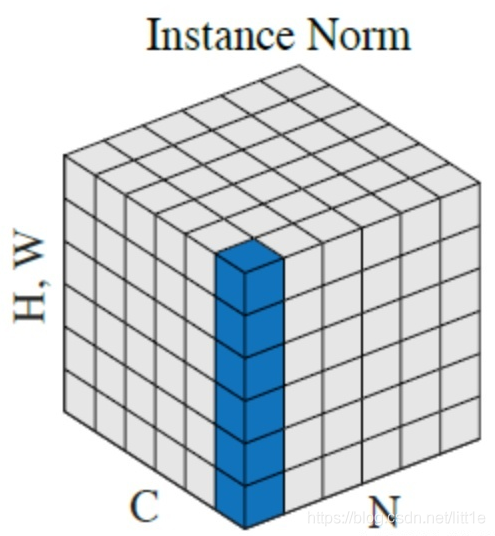
上图中,从C方向看过去是指一个个通道,从N看过去是一张张图片。每6个竖着排列的小正方体组成的长方体代表一张图片的一个feature map。蓝色的方块是一起进行Normalization的部分。由此就可以很清楚的看出,Batch Normalization是指6张图片中的每一张图片的同一个通道一起进行Normalization操作。而Instance Normalization是指单张图片的单个通道单独进行Noramlization操作。
版权声明:本文为CSDN博主 “小小小绿叶” 原创文章,
遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/litt1e/article/details/105817224






