卷积是一种数学运算,它采用某种方式将一个函数“应用”到另一个函数。结果可以理解为两个函数的“混合体”。卷积由一个星号 (*) 表示,这可能与许多编程语言中通常用于乘法的 * 运算符混淆。
不过,这对检测图像中的目标有何帮助?事实证明,卷积非常擅长检测图像中的简单结构,然后结合这些简单特征来构造更复杂的特征。在卷积网络中,会在一系列的层上发生此过程,每层对前一层的输出执行一次卷积。
那么,您会在计算机视觉中使用哪种卷积呢?要理解这一点,首先必须了解图像到底是什么。图像是一种二阶或三阶字节数组,二阶数组包含宽度和高度两个维度,三阶数组有 3 个维度,包括宽度、高度和多个通道。所以灰阶图是二阶的,而 RGB 图是三阶的(包含 3 个通道)。字节的值被简单解释为整数值,描述了必须在相应像素上使用的特定通道数量。所以基本上讲,在处理计算机视觉时,可以将一个图像想象为一个 2D 数字数组(对于 RGB 或 RGBA 图像,可以将它们想象为 3 个或 4 个 2D 数字数组的相互重叠)。
因此,我的卷积获取此数组(我暂时假设该图是灰阶的),并将它与第二个数组(一个过滤器)进行卷积运算。卷积过程如下。首先,将过滤器叠加在图像数组的左上部。接下来,对过滤器及其目前所在的图像子部分执行对应元素乘积。也就是说,将过滤器的左上部元素与图像的左上部元素相乘,依此类推。然后,将这些结果相加来生成一个值。接着,将过滤器在图像上移动一段距离(称为步幅),并重复该过程。此过程的输出是一个具有与图像数组不同维数的新数组(结果通常具有更小的宽度和高度,但包含更多的通道)。为了演示卷积运算的工作原理,让我们来看一个示例。这是一个 3 x 3 过滤器:
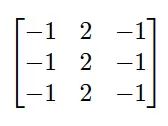
我将把这个过滤器应用到下图。
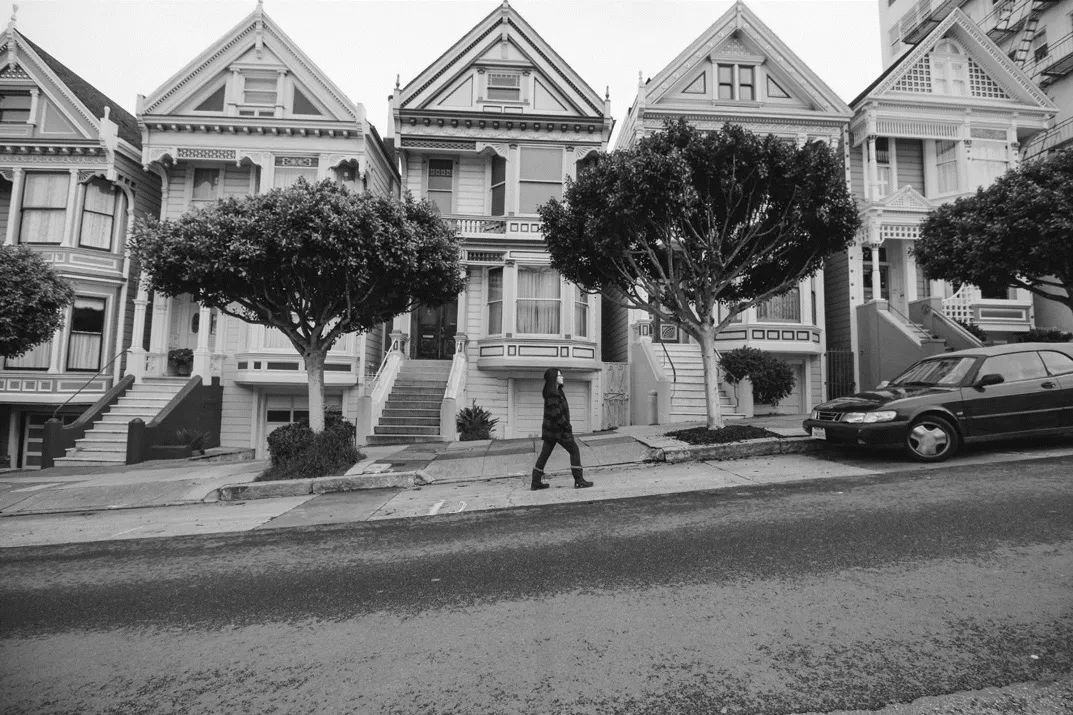
向此图应用了一轮过滤器后,我获得了以下结果。

希望您可以看到,过滤器似乎将各个值垂直排列。这意味着它辨别出了图像中的垂直特征,这一点可以在结果中看到。这是一个在运行 CNN 时学到的过滤器值。
应该注意的是,步幅和过滤器大小是超参数,这意味着模型不会学习它们。所以您必须应用科学思维来确定这些数量中的哪些值最适合您的应用程序。
对于卷积,您需要理解的最后一个概念是填充。如果您的图像无法在整数次内与过滤器拟合(将步幅考虑在内),那么您必须填充图像。可通过两种方式实现此操作:VALID 填充和 SAME 填充。基本上讲,VALID 填充丢弃了图像边缘的所有剩余值。也就是说,如果过滤器为 2 x 2,步幅为 2,图像的宽度为 3,那么 VALID 填充会忽略来自图像的第三列值。SAME 填充向图像边缘添加值(通常为 0)来增加它的维数,直到过滤器能够拟合整数次。这种填充通常以对称方式进行的(也就是说,会尝试在图像的每一边添加相同数量的列/行)。
同样值得注意的是,图像卷积的用途并不仅限于计算机视觉。许多图像过滤技术都可以使用卷积来实现,比如模糊化和锐化。
下面的基本 Python 代码展示了卷积运算的工作原理(您可以让此代码变得更简洁,比如通过使用 numpy):
def basic_conv(image, out, in_width, in_height, out_width, out_height, filter,
filter_dim, stride):
result_element = 0
for res_y in range(out_height):
for res_x in range(out_width):
for filter_y in range(filter_dim):
for filter_x in range(filter_dim):
image_y = res_y + filter_y
image_x = res_x + filter_x
result_element += (filter[filter_y][filter_x] *
image[image_y][image_x])
out[res_y][res_x] = result_element
result_element = 0
res_x += (stride - 1)
res_y += (stride - 1)
return out请注意,如果希望将结果写到图像文件中(像我上面那样对它进行可视化),则必须限制输出值,使它们不超过 255。