1. 前言戏说
双目立体视觉是基于视差原理,由多幅图像获取物体三维几何信息的方法。在机器视觉系统中,双目视觉一般由双摄像机从不同角度同时获取周围景物的两幅数字图像,或有由单摄像机在不同时刻从不同角度获取周围景物的两幅数字图像,并基于视差原理即可恢复出物体三维几何信息,重建周围景物的三维形状与位置。
双目视觉有的时候我们也会把它称为体视,是人类利用双眼获取环境三维信息的主要途径。从目前来看,随着机器视觉理论的发展,双目立体视觉在机器视觉研究中发回来看了越来越重要的作用。本篇帖子主要研究了双目视觉的数学原理。
2. 双目立体视觉的数学原理
双目立体视觉是基于视差,由三角法原理进行三维信息的获取,即由两个摄像机的图像平面和北侧物体之间构成一个三角形。一直两个摄像机之间的位置关系,便可以获得两摄像机公共视场内物体的三维尺寸及空间物体特征点的三维坐标。所以,双目视觉系统一般由两个摄像机构成。
2.1 双目立体视觉三维测量原理
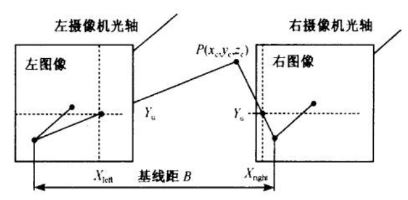
上图所示为简单的平视双目立体成像原理图,两摄像机的投影中心连线的距离,即基线距离B。两摄像机在同一时刻观看时空物体的同一特征点P,分别在“左眼”和“右眼”上获取了点P的图像,他们的坐标分别为Pleft=(Xleft,Yleft);Pright=(Xright,Yright)。将定两摄像机的图像在同一平面上,则特征点P的图像坐标的Y坐标一定是相同的,即Yleft = Yright =Y。由三角几何关系可以得到如下关系式:
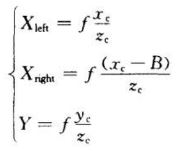
则视差为:Disparity=Xleft-Xright.由此可以计算出特征点P在摄像机坐标系下的三维坐标:

因此,左摄像机像面上的任意一点只要能在右摄像机像面上找到对应的匹配点,就完全可以确定该点的三维坐标。这种方法是点对点的运算,像平面上所有点只要存在相应的匹配点,就可以参与上述运算,从而获取对应的三维坐标。
2.2 双目立体视觉数学模型
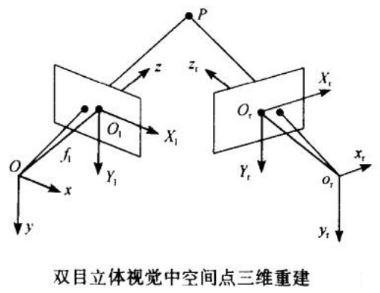
在分析了最简单的平视双目立体视觉的三维测量原理基础上,现在我们就有能力来考虑一般情况。如上图所示,设左摄像机O-xyz位于世界坐标系原点,且没有发生旋转,图像坐标系为Ol-X1Y1,有效焦距为fl;右摄像机坐标系为Or-xyz,图像坐标系为Or-XrYr,有效焦距为fr。那么根据摄像机的投射模型我们就能得到如下关系式:
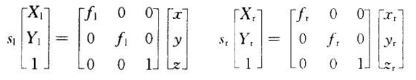
因为O-xyz坐标系与Or-xryrzr坐标系之间的位置关系可通过空间转换矩阵MLr表示为:

同理,对于O-xyz坐标系中的空间点,两个摄像机面点之间的对应关系可以表示为:
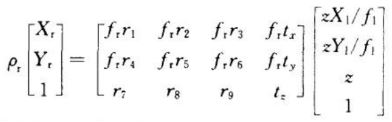
于是,空间点三维坐标可以表示为
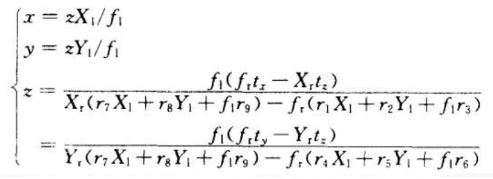
因此,只要我们通过计算机标定技术获得左右计算机内参数/焦距fr,fl和空间点在左右摄像机中的图像坐标,就能够重构出被测点的三维空间坐标。
版权声明:本文为CSDN博主「沈子恒」的原创文章,
遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/shenziheng1/article/details/52883536






