引言
Dynamic Programming, Monte Carlo, Temporal Difference是强化学习过程中最基础的三种算法,本文主要总结一下这三种方法的区别与联系;
强化学习模型本质上是一个随机过程,可以用概率图模型来描述,就像 HMM 可以使用有向图来描述,马尔可夫网可以使用无向图来描述,强化学习对应的图模型是Finite Markov Decision Process(MDP),如下图(也被称作智能体-环境交互模型):

强化学习主要分为两步工作,第一步,预测每个状态的value function或Q function,第二步,根据value function或Q function生成Policy;
Dynamic Programming
MDP模型已知,使用贝尔曼方程进行迭代求解value function:


学习算法一般使用GPI(Generalized Policy Iteration),及policy evaluation和policy improvement同时进行,最终找到 optimal value function和optimal policy。policy evaluation过程使用的是bootstrap方法,向前传播;

Monte Carlo 回合更新
MDP模型未知,通过回合制(episode)采样来计算value function

每遍历完一个episode,就进行Q function更新:
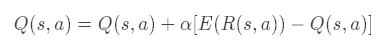
或value function更新:

E(R(s,a))表示一个episode内的(s,a) (s,a)(s,a)对应的回报的期望,E(R(s)) E(R(s))E(R(s)) 表示一个episode内的 s ss 对应的回报的期望,α \alphaα表示学习率;
例如:On-policy First-visit MC control algorithm

Temporal Difference 单步更新
MDP模型未知,通过回合制(episode)采样来计算value function,与MC的区别是,每执行完episode中的一步就进行更新;
更新方法:

TD方法结合了 DP 的bootstrap和 MC 的sampling
典型算法:Sarsa(On-policy TD Control)、Q-Learning(Off-policy TD Control)、Sarsa(λ \lambdaλ)等
总结
TD结合了MC的sampling方法和DP的bootstrap方法,是空间复杂度和时间复杂度都最低的算法,是大型状态空间问题的唯一解决方案;
MC收敛于样本的无偏估计,TD收敛于样本的确定等价估计;
版权声明:本文为CSDN博主「吃龙虾一样能吃饱」的原创文章,
遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_36013249/article/details/105868739






