一、KNN算法原理
K近邻法(k-nearst neighbors,KNN)是一种很基本的机器学习方法。
它的基本思想是: 在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类。
由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成反比。
KNN算法的描述:
(1)计算测试数据与各个训练数据之间的距离;
(2)按照距离的递增关系进行排序;
(3)选取距离最小的K个点;
(4)确定前K个点所在类别的出现频率
(5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
算法流程:
(1) 准备数据,对数据进行预处理。
(2)选用合适的数据结构存储训练数据和测试元组。
(3)设定参数,如k。
(4)维护一个大小为k的的按距离由大到小的优先级队列,用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存入优先级队列。
(5)遍历训练元组集,计算当前训练元组与测试。元组的距离,将所得距离L 与优先级队列中的最大距离Lmax。
(6)进行比较。若L>=Lmax,则舍弃该元组,遍历下一个元组。若L < Lmax,删除优先级队列中最大距离的元组,将当前训练元组存入优先级队列。
(7)遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
(8)测试元组集测试完毕后计算误差率,继续设定不同的k值重新进行训练,最后取误差率最小的k 值。
算法优点:
(1)简单,易于理解,易于实现,无需估计参数。
(2)训练时间为零。它没有显示的训练,不像其它有监督的算法会用训练集train一个模型(也就是拟合一个函数),然后验证集或测试集用该模型分类。KNN只是把样本保存起来,收到测试数据时再处理,所以KNN训练时间为零。
(3)KNN可以处理分类问题,同时天然可以处理多分类问题,适合对稀有事件进行分类。
(4)特别适合于多分类问题(multi-modal,对象具有多个类别标签), KNN比SVM的表现要好。
(5)KNN还可以处理回归问题,也就是预测。
(6)和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感。
算法缺点:
(1)计算量太大,尤其是特征数非常多的时候。每一个待分类文本都要计算它到全体已知样本的距离,才能得到它的第K个最近邻点。
(2)可理解性差,无法给出像决策树那样的规则。
(3)是慵懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢。
(4)样本不平衡的时候,对稀有类别的预测准确率低。当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
(5)对训练数据依赖度特别大,对训练数据的容错性太差。如果训练数据集中,有一两个数据是错误的,刚刚好又在需要分类的数值的旁边,这样就会直接导致预测的数据的不准确。
二、代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs #make_blobs 聚类数据生成器
from sklearn.neighbors import KNeighborsClassifier #KNeighborsClassfier K近邻分类
#sklearn 基于Python语言的机器学习工具,支持包括分类,回归,降维和聚类四大机器学习算法。
# 还包括了特征提取,数据处理和模型评估者三大模块。
# sklearn.datasets (众)数据集;sklearn.neighbors 最近邻
data=make_blobs(n_samples=5000,centers=5,random_state=8)
# n_samples 待生成样本的总数,sample 样本,抽样
# centers 要生成的样本中心数
# randon_state 随机生成器的种子
X,y=data
#返回值,X 生成的样本数据集;y 样本数据集的标签
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
#c颜色,cmap Colormap实体或者是一个colormap的名字,cmap仅仅当c是一个浮点数数组的时候才使用。
clf=KNeighborsClassifier()
clf.fit(X,y)
x_min,x_max=X[:,0].min()-1,X[:,0].max()+1
y_min,y_max=X[:,1].min()-1,X[:,1].max()+1
xx,yy=np.meshgrid(np.arange(x_min,x_max,0.02),
np.arange(y_min,y_max,0.02))
Z=clf.predict(np.c_[xx.ravel(),yy.ravel()])
Z=Z.reshape(xx.shape)
plt.pcolormesh(xx,yy,Z,cmap=plt.cm.Pastel1)
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
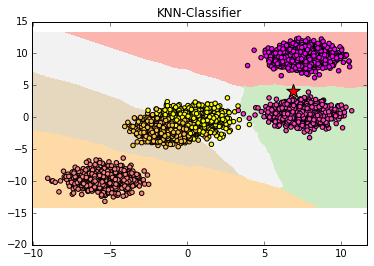
plt.title('KNN-Classifier')
plt.scatter(6.88,4.18,marker='*',s=200,c='r')
plt.xlim([x_min,x_max])
print('模型建好后的运行结果如下:')
print('=======================')
print('新加入样本的类别是:',clf.predict([[6.72,4.29]]))
print('该模型针对次数据集的分类正确率是:{:.2f}'.format(clf.score(X,y)))输出结果:
模型建好后的运行结果如下:
=======================
新加入样本的类别是: [1]
该模型针对次数据集的分类正确率是:0.96
本文转自:博客园 - 泰初,转载此文目的在于传递更多信息,版权归原作者所有。






